정상상태 전류 5-1, 5-2 Ohm's Law

Current Density, Ohm's Law

이전까지는 어떤 근원전하(Source)에 의한 $\mathbf{F}$, $\mathbf{E}$, $\mathbf{D}$, $V$, $W_e$에 대하여 봤다.

5 장에서는 $\mathbf{E}$가 형성되어 있는 매질 내에서 전기장의 영향을 받아 이동하는 이동전하와 전류의 형성에 대해 본다. 물론 정상상태(steady state)인 경우를 주로 봄

전류는 전도성 전류, 전해성 전류, 대류성 전류로 나뉘는데

전도성 전자 및 정공의 이동에 기인하는 전도성 전류($\mathbf{J_c}[A/m^2]$)에 대해서 주로 본다.

전류는 시간에 따른 전하의 변화율이다.

• $\Delta I=\frac{\Delta Q}{\Delta t}$

여기서 $\Delta Q=Nq\Delta V$로 볼 수 있으므로,

• $\Delta I=Nq \frac{\Delta V}{\Delta t}$ [A]=[C/s]

여기서 단위시간당 흐르는 물체의 체적인 체적유량${\Delta V}/{\Delta t}$을 생각해보면
전하량이 q인 한 가지 종류의 전하 캐리어가 $u$의 속도를 가진다고 하면,

• ${\Delta V}/{\Delta t}=NquS=Nq\mathbf{u}\cdot\Delta\mathbf{s}$

면에 수직이 아닐 수도 있으므로 벡터 형식이 더 일반적이다.

• $\Delta I=Nq\mathbf{u}\cdot\Delta\mathbf{s}$

벡터 점함수인 체적전류밀도/전류밀도를 정의한다.

• $\mathbf{J}=Nq\mathbf{u} [A/m^2]$ 로 정의한다.

• $\Delta I=\mathbf{J}\cdot\Delta\mathbf{s}$

이를 임의의 면적에 대해 적분하면 전체 전류 I는

• $I=\int_s\mathbf{J}\cdot d\mathbf{s} [A]$

만약 자유전하에 대해 볼 경우 $Nq=\rho$이므로 $\mathbf{J}=\rho\mathbf{u}$ 이다.
$\mathbf{J}=\rho\mathbf{u}$ (대류성 전류밀도)
대류성 전류밀도에 대한 것은 예제 5-1로 확인해본다.

---

---

---

그런데 지금 5장에서는 자유전하의 이동에 의한 전도성 전류에 집중하므로

• $\mathbf{J}_c$: Conduction Current(전도성 전류)

전도성 전류는 인가된 전기장에 의해 전하 캐리어가 정전기적 힘을 받아서 전하가 이동하고 전류를 형성하는 Drift current이다.

• $\mathbf{E}->\mathbf{F}->Drift$(전하이동) $-> Current$ 형성

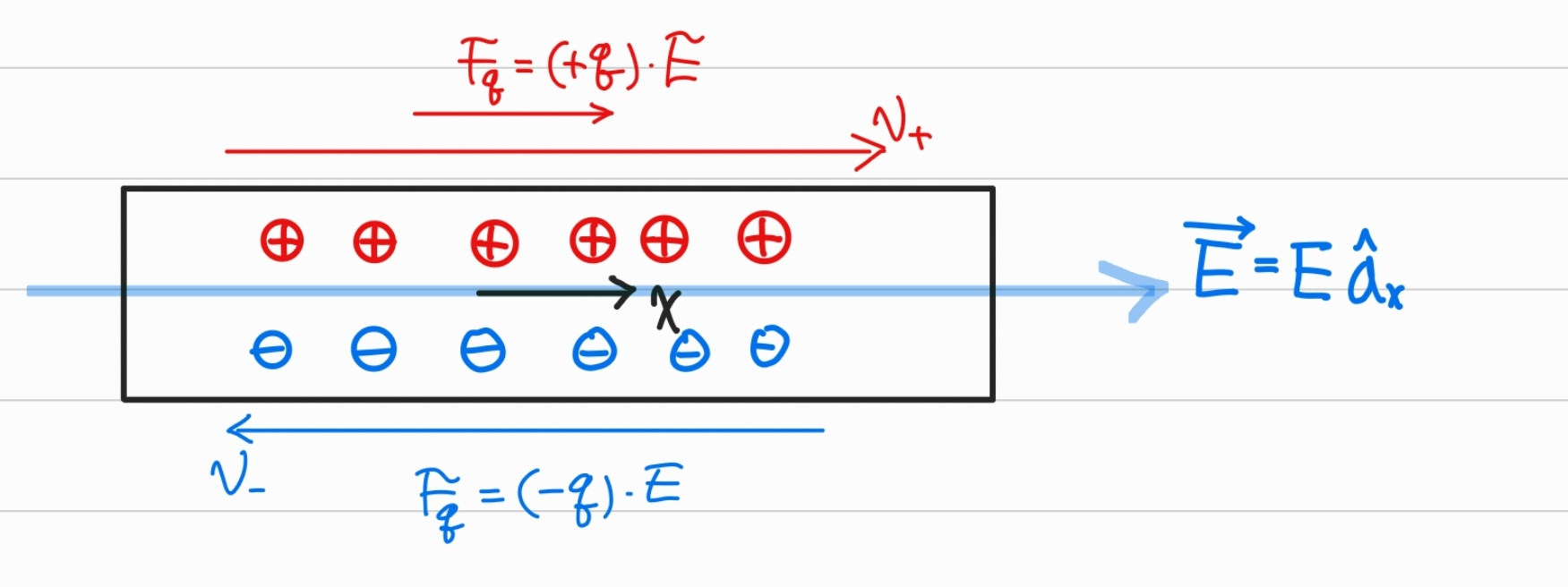
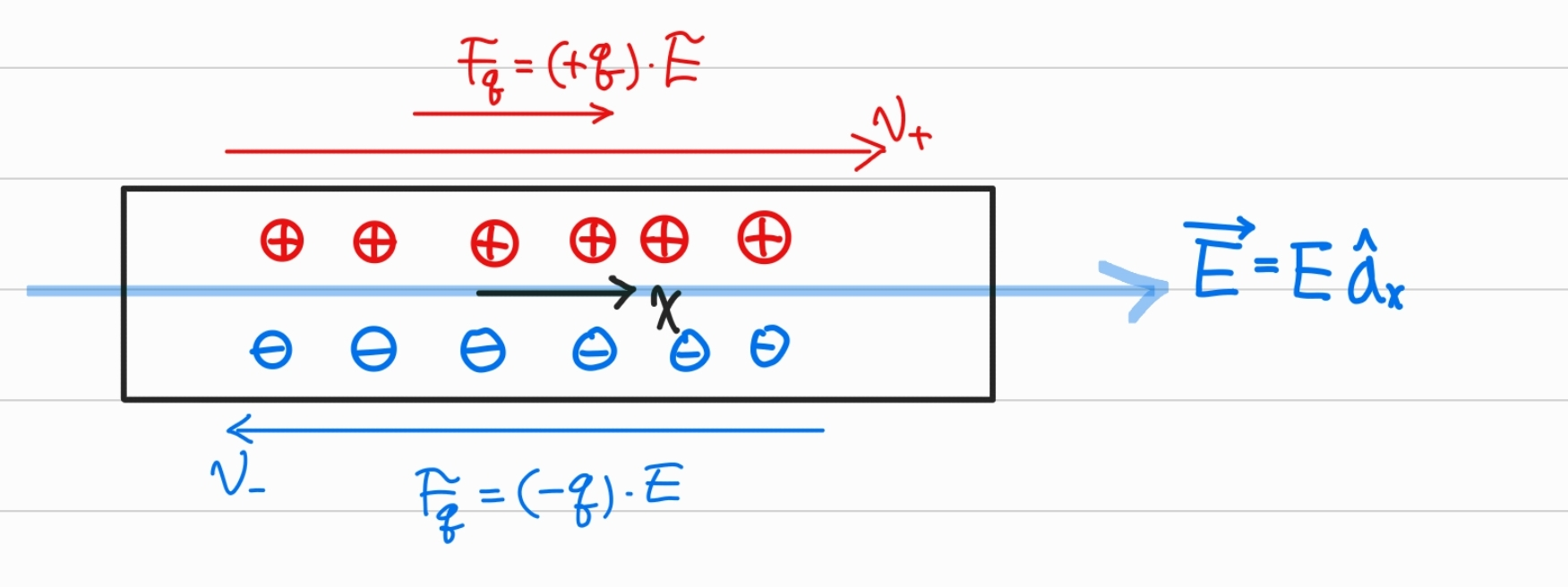
다음과 같이 어떤 도체에 두 종류의 전하가 존재한다고 하자.
1) 전기장이 $+x$축 방향으로 가해지면

2) $+q$ 전하는 $+x$로 음전하는 $-x$로 정전기력을 받아서

3) Drift하게 될 것이다. (방향 반대)

대부분의 도체에서 전기장의 세기와 평균 드리프트 속도는 비례한다.

• $\mathbf{v}=\mu\mathbf{E}$
  이 비례 상수를 $\mu$, 이동전하의 이동도라고 한다.
  $\mu$ 는 매질(재료)에 의해 결정되는 상수이다.

전도성 전류밀도는 드리프트 이동을 하는 이동전하의 밀도와 속도의 곱의 합으로 구성된다.

• $\mathbf{J_c}=\rho_{m+}\mathbf{v_{+}}+\rho_{m-}\mathbf{v_{-}}$

$\rho_{m-}<0$,
$\mathbf{v_{-}}<0$
이므로

• 양전하에 의한 Drift current와 음전하에 의한 그것과 방향이 같다.

$\mathbf{v}=\mu\mathbf{E}$ 이므로
$\mathbf{J_c}=\rho_{m+}\mathbf{v_{+}}+\rho_{m-}\mathbf{v_{-}}$

• 전도성 매질에 의한 전류 방정식 or Point Form of Ohm's Law

$\mathbf{J_c}=(\rho_{m+}\mu_{p}+\rho_{m-}\mu_{n})\mathbf{E}=\sigma\mathbf{E}$

여기서 $\sigma$를 전기전도도라고 한다.
풀어서 설명하면 전기전도도는 각 (전하캐리어의 밀도)$\times$(전기장에 의한 Drift속도)의 합으로 구성된다.
이 식이 성립하는 등방성 매질을 저항성 매질(Ohmic media)라고 함.

• 아주 간단한 예시를 통해 Point Form에서 균질 도체로 적용했더니 회로이론에서의 공식을 볼 수 있었다.