정상상태 전류 5-3 기전력

기전력

비보존력 원천의 세기에 대한 척도이다.

당장 필요할 거 같지 않아서 패스하려 했지만 그냥 궁금해서 작성

책의 그림이 너무 이해가 안되서 다시 그렸다...

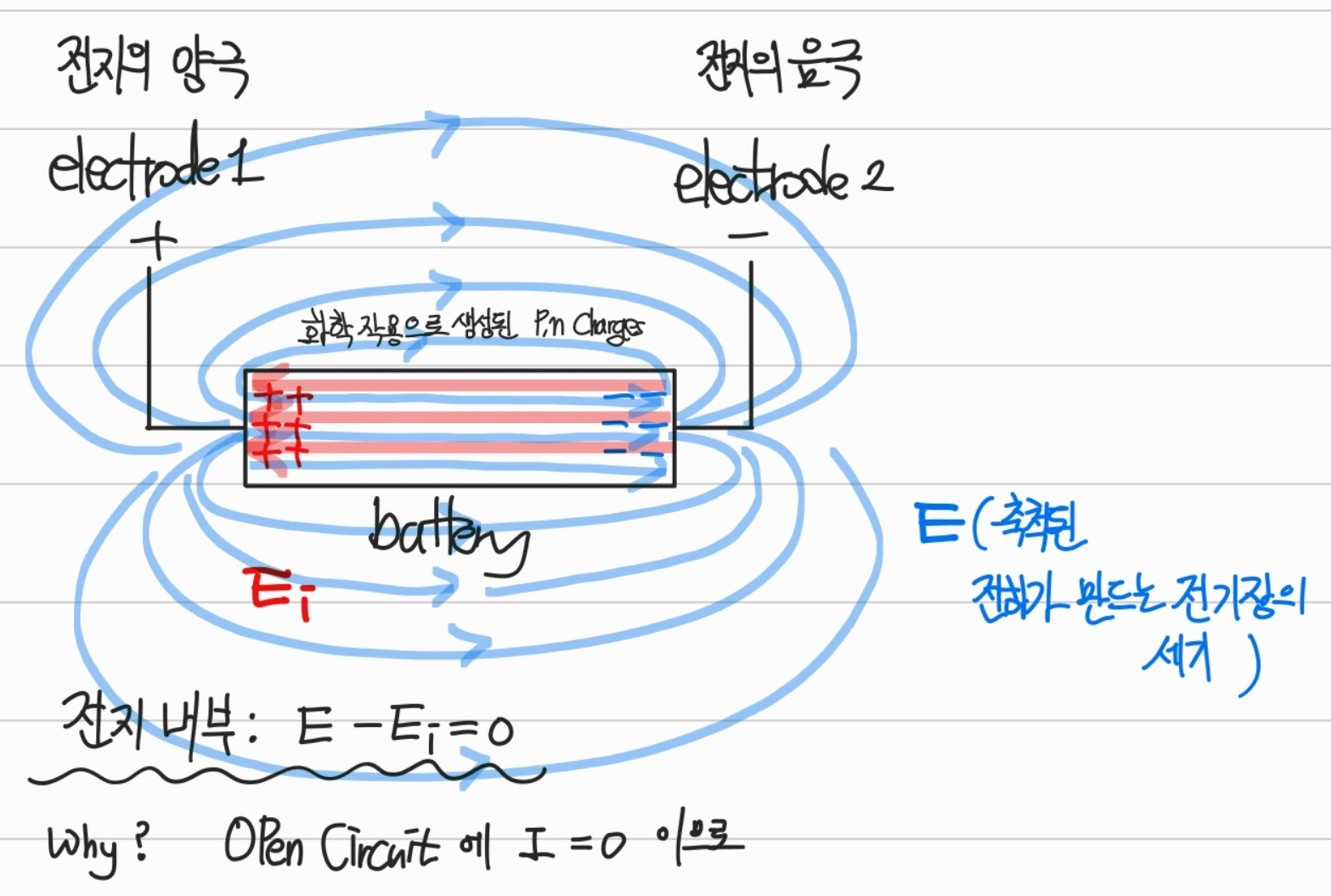
• 전지의 양극은 연결되지 않은 Open Circuit인 상태이고 전류가 흐르지 않기 때문에 전지 내부의 전기장은 없다.

전하 캐리어에 작용하는 net force가 사라지므로 전류가 흐르지 않음

• 전하가 축척되는 것은 그냥 받아들이기로 했다.
  전기화학적인 반응으로 인해서 자발적으로 축척되는 것이라는데 잘 모르기에

축척된 전하에 의한 전기장은 보존적이다

• 화학작용에 의해 발생된 $\mathbf{E}_i$는 비보존력이고 $\mathbf{E}$와 크기는 같고 방향은 반대이다.

• 기전력: 비보존력 원천의 세기에 대한 척도이다.

  $\mathcal{V}=\int^1_2\mathbf{E}_i \cdot d\mathbf{l}=\int^2_1\mathbf{E} \cdot d\mathbf{l}$

기전력의 비보존적 특성에도 불구하고 전압으로 나타낼 수 있다.

$\mathcal{V}=\int^2_1\mathbf{E} \cdot d\mathbf{l}$ ; (Outside the source,전지 바깥쪽에서 선적분)

$\mathcal{V}=V_1-V_2=V_{12}$

저항이 연결된다면 총 전기장의 세기는 Ohm's Law에 의해서..

• $\mathbf{J}=\sigma(\mathbf{E}+\mathbf{E_i})$

주의해야 할 점은 $\mathbf{E_i}$는 전지 내부에만 존재하는 것이다.

$\mathcal{V}=\int^2_1(\mathbf{E}+\mathbf{E_i}) \cdot d\mathbf{l}=\int^2_1\mathbf{E_i} \cdot d\mathbf{l}=\oint_c\frac{1}{\sigma}\mathbf{J}\cdot d\mathbf{l}$

만약 면적S,길이L,인 균질한 저항이 연결된다면 J=I/A 이므로

$\mathcal{V}=RI$ 이고
이는 회로이론에서의 키르히호프의 전압법칙에 해당한다.

(Open Circuit) 연결되어 있지 않은 경우에 정의된 것이 기전력이고,
저항이 연결된다면 선적분을 통해 V=RI라는 공식이 나오는 것이다.