정자기장 6/4 자기쌍극자

	전기장	자기장
요소	켤레 전하의 존재	아주 작은 폐경로의 전류 도선
쌍극자	전하쌍극자	자기쌍극자
쌍극자의 집합체	유전체	자성체
집합체의 특성	분극	자화
재료 특성	유전상수/상대유전율 $\epsilon_r$	상대투자율 $\mu_r$
	유전율 $\epsilon$	투자율 $\mu$
	$\mathbf{D}=\epsilon \mathbf{E}$	$\mathbf{B}=\mu \mathbf{H}$

전기장 파트에서는 유전체의 분극 등 유전체와 유전상수에 대해 알아보았다.

자기장에 관련해서는 자기장이 인가되기 전과 후의 자성체의 특성에 대해 살펴본다.

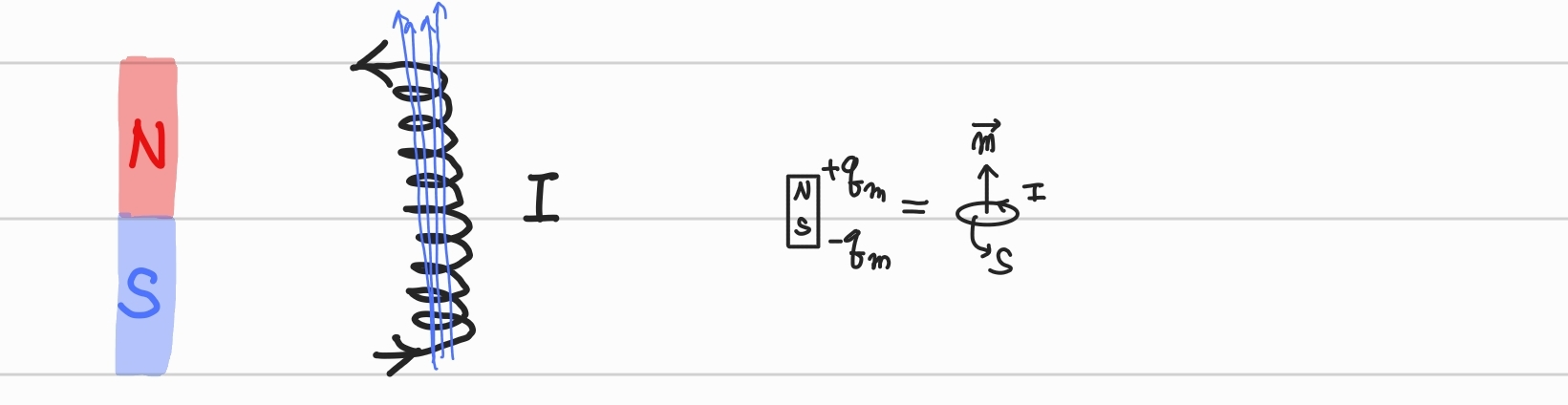
전하쌍극자 vs 자기쌍극자

전하쌍극자는 양전하와 음전하가 켤레로 존재하는 것을 말했다.

그렇다면 자기쌍극자는 뭘까?

자기쌍극자는 아주 작은 폐경로 형태의 전류 도선을 말한다.

궤도를 도는 전자는 회전하는 전류를 발생시키고 미시적인 자기 쌍극자를 발생시킨다.

또한 전자와 원자핵 자체도 어느정도의 자기쌍극자 모멘트를 가지고 Spin을 한다.

외부 자기장의 인가로 인한 전자 궤도 운동 변화에 의한 자기모멘트인 유도자기모멘트 와 자전하는 전자들의 자기 모멘트가 있다.

편리하게 하기 위해 원자 하나의 자기 쌍극자 모멘트를 $\mathbf{m_i}$ 라고 하자.

자석의 근원

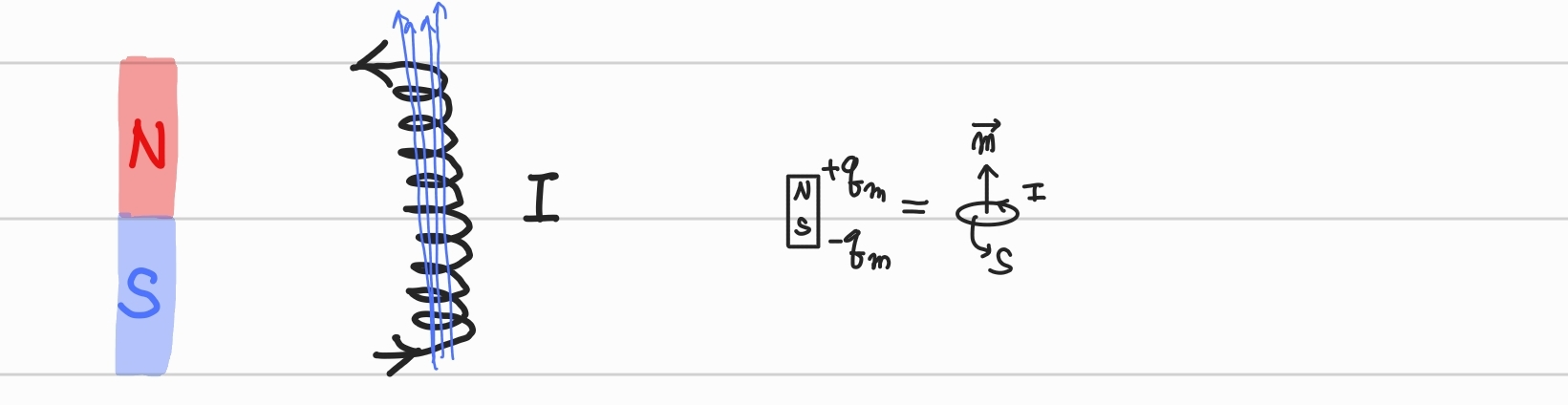
물리학자들은 자석의 근원이 전자의 운동임을 알게 되었다.

유전체에서 자기쌍극자들의 집합체 중 가장 작은 단위를 만들면 그것이 전하쌍극자였고,

자성체의 경우에는 미시적인 순환전류라고 볼 수 있다.

독립된 자하는 존재하지 않지만, 아주 작은 막대 자석의 끝에 가상의 자하들이 놓여 있다고 해석하면 편리하다.

자성체

(자화 벡터를 정의하기위해 간단한 상자성체(Paramagnetic)의 경우로 봄)
자성체를 균일한 자기쌍극자의 특성을 가진 물체로 정의한다.

1) 자성체가 외부 자기장이 인가되기 전

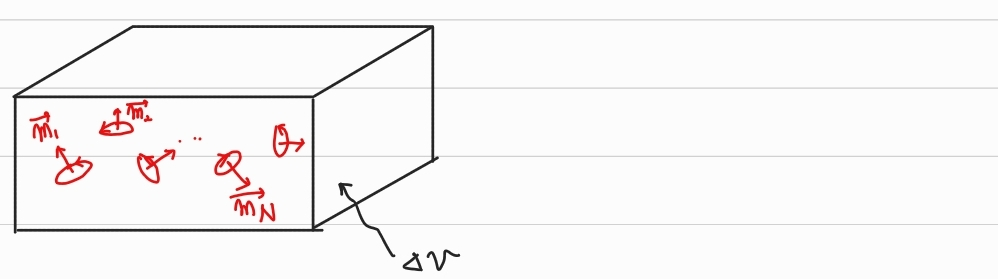
이때 자성체 내의 각 원자들의 자기쌍극자는 Random Orientation을 가지고 있다.

$\mathbf{m_1}+\mathbf{m_2}+\mathbf{m_3} \dots+\mathbf{m_n}=0 [A \cdot m]$

2) 자성체가 외부 자기장이 인가 되고

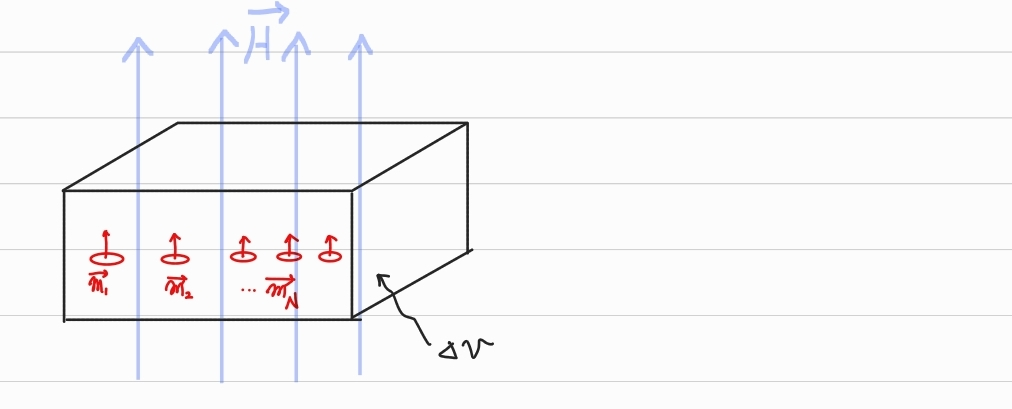
자기쌍극자에 작용하는 토크

$\mathbf{T}=\mathbf{m_i}\times \mu\mathbf{H}$ 이므로 각 자기쌍극자들은 외부 자기장의 방향으로 정렬한다.

이 과정을 자화(magnetization)라고 한다.

분극이 일어난 후에 모든 자기쌍극자모멘트 벡터는 같아진다.

$\mathbf{m_1}=\mathbf{m_2}=\mathbf{m_3} =\dots=\mathbf{m_n}$

자화벡터를 정의하면,

$\mathbf{M}\triangleq\frac{\displaystyle \sum^N \mathbf{m_i}}{\Delta V}=N\mathbf{m}/\Delta V=n_{mdp}\mathbf{m}$ 단위는 $[A / m]$: $\mathbf{H}$와 단위가 같음.

• N은 자성체 내의 $\Delta V$의 자기쌍극자의 총 개수이며

• $\mathbf{m}$은 개별 자기쌍극자 모멘트이다.

• 자기쌍극자의 농도 $n_{mdp}=N/\Delta V$로 정의할 수 있다.

3) 자화 후의 자화 벡터는 자기장의 세기와 비례한다.

$\mathbf{M} \propto \mathbf{H}$
그 비례상수를 $\chi_m$ ; 카이 m로 정의한다.

$\mathbf{M}=n_{mdp}\mathbf{m}\mathbf{a}_H=n_{mdp}\mathbf{m}\frac{\mathbf{H}}{|H|}$

$\mathbf{M}=\chi_m\mathbf{H}$ 단위 $[A/m]$

4) 자화 후의 자성체 내의 자속밀도와 상대적 투자율

자성체 밖의 자속밀도 $\mathbf{B}_{ext}=\mu_0\mathbf{H}$ 이다.

그런데 자성체 내의 정렬된 자기쌍극자들은 작은 흐르는 폐경로의 전류이므로 또한 자기장을 생성한다.

따라서 자성체 내의 자속밀도는

• $\mathbf{B}_{paramagnatic}=\mathbf{B}_{ext} + \mathbf{B}_{by \space mdp}$

• $\mathbf{M} \propto\mathbf{H}$ 이므로, $\mathbf{M} \propto\mathbf{B}$ 일 것이다.

따라서

• $\mathbf{B}_{by \space mdp} =\mu_0 \chi_m\mathbf{M}$
  이다.

$\mu_0$ 는 자속밀도와 분극벡터간의 단위를 맞추는 데에 사용되었다고 봐도 된다.
$\chi_m$는 재료에 따른 값이므로 저렇게 봐도 무방하다.

상대적 투자율
$\mu_r=\mu_0 \chi_m$
$\mu_r, \chi_m$는 자성체가 외부 자기장에 얼마나 민감한 지의 지표이다.
즉, 자화가 얼마나 더 많이 되는가에 대한 것이다.

이렇게 절대투자율 $\mu$를 이용한 자속밀도를 드디어 정의하였다.

자속의 단위는 $Wb/m^2$ 인데 여기서 $Wb=H \cdot A$ 이다. Flux를 나타낸다는 정도만 알아두면 될 것 같다.