정자기장 6/3 Lorentz Force Equation

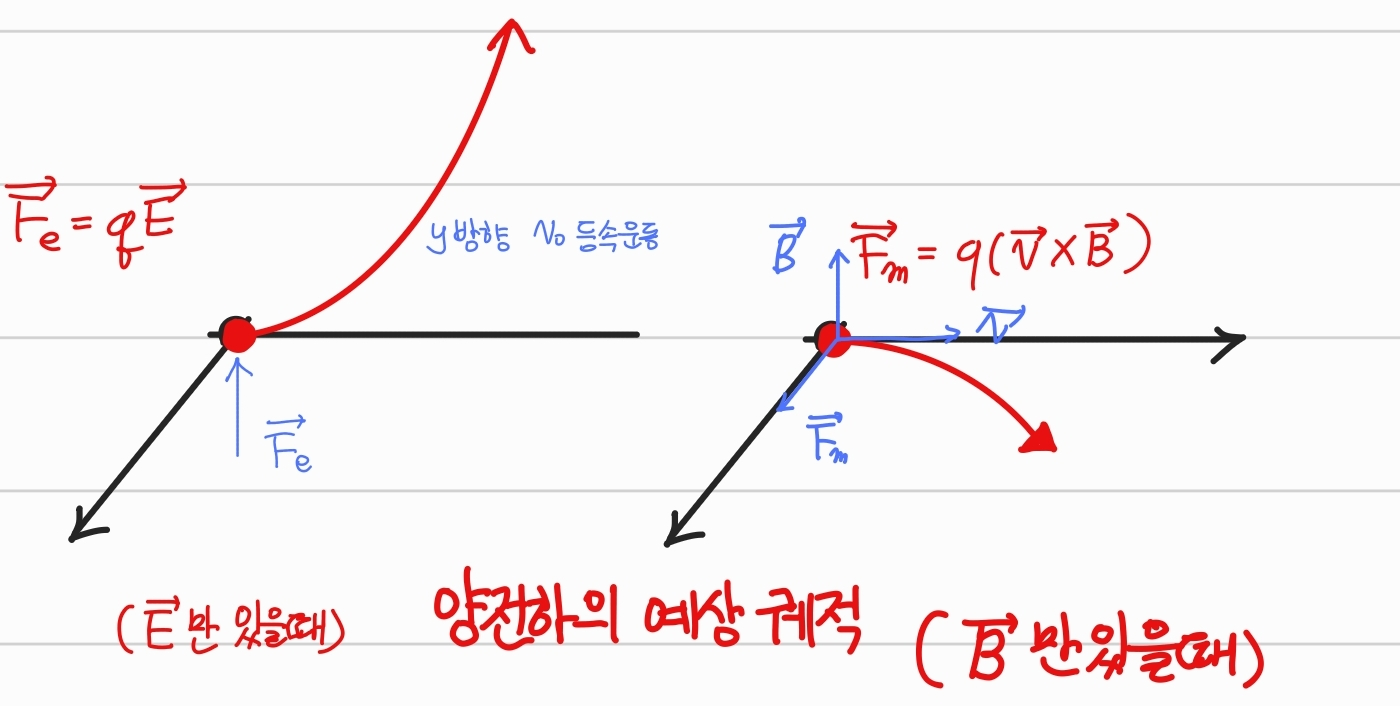
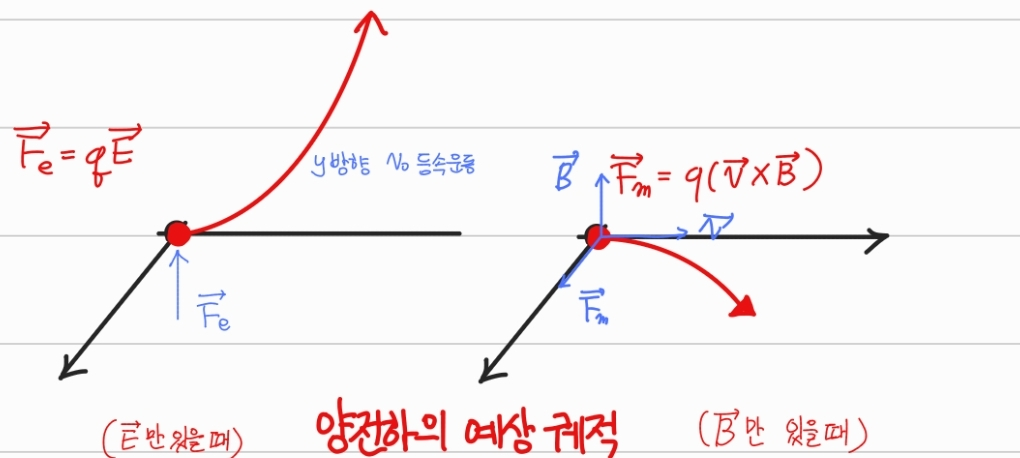
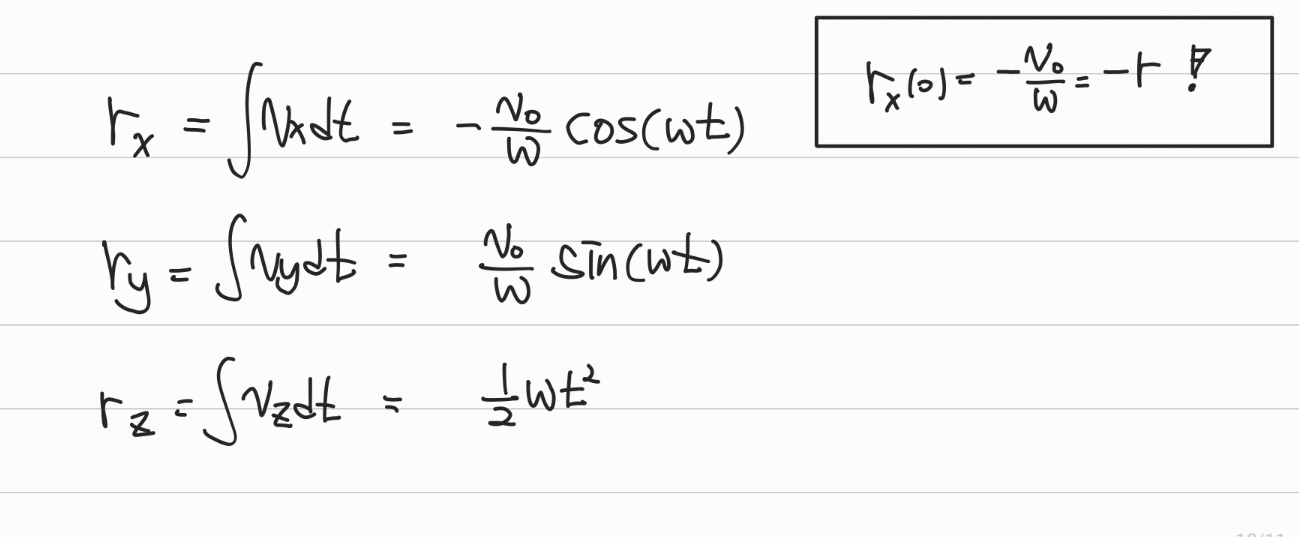전기장이 작용하는 공간 내에 존재하는 미소전하 q에 작용하는 힘은
전기력 $\mathbf{F}_e=q\mathbf{E}$ 가 작용한다.

---

이와 마찬가지로 자기력 $\mathbf{F}_m$에 대해 살펴본다.

흐르는 전류에 의해 미소전류도선에 작용하는 힘에 대해 이전에 살펴보았다. 이식은

• $\mathbf{F} = \mu \, \textcolor{blue}{[I_t d\mathbf{L_t}]} \times \textcolor{red}{[\frac{I_s d\mathbf{L_s}}{4\pi R^2} \times \mathbf{a_R}]}$

$\textcolor{blue}{[I_t d\mathbf{L_t}]}$ Units $[A \cdot m]=[C \cdot m/s]$

여기서 $\mathbf{H}$는 어떻게든 주어진 값인 것이고,
단위에서부터 알 수 있듯이 시험전류도선처럼
움직이는 시험전하는 형성된 자기장에 영향을 받음을 알 수 있다.
따라서

• $\mathbf{F}_m = q\mathbf{v}\times \mathbf{B}$

아직 정의하지는 않았지만, $\mathbf{B}=\mu \mathbf{H}$ $[Wb/m^2]$이다.
Wb가 뭔지 모르지만, 단위를 보면 Flux의 형태임을 짐작할 수 있다.

마지막으로 전기장과 자기장이 모두 존재할 때에 시험전하가 받는 힘은 Loretnz Force Equation으로 정리할 수 있다.

• $\mathbf{F}=q(\mathbf{E}+\mathbf{v}\times \mathbf{B})$

---

다음으로 전기장과 자기장이 주어졌을 때 어떤 시험입자의 움직임을 살펴본다.

어떤 아주 전하량이 작은 양전하가 균일한 자기장 영역에 $\mathbf{v_0}=v_0\mathbf{a}_y$ 의 속도로 입사되었다.

Z축과 평행한 방향으로 전기장과 자기장이 인가되었다.
중력을 무시한다고 가정하면,

$\mathbf{v}=\mathbf{v}_{z}+\mathbf{v}_{x-y}$ 로 나눌 수 있고, 구심가속도에 기여하는 속도는 $\mathbf{v}_{x-y}$이다.

간단하게 $\mathbf{v}_{\perp}$ 으로 나타내면,

• $F_m=qv_{\perp}B=mv_{\perp}^2/r$

• $v_{\perp}=(qB/m)r$

원의 중심으로 원점을 옮기면 다음과 같이 적을 수 있다.

• $v_{\perp}=r \omega$
  $\omega=qB/m$
  으로 적도록 한다.

또한 전기력에 의한 양전하의 움직임에 대해서는 자기장에 의한 원운동을 방해하지 않고 $z$방향으로만 가속시킨다는 것을 알 수 있다. ($z$ 움직임에만 관여) 따라서 양전하에 대해 FBD를 그리고 이로 미분방정식을 풀면.

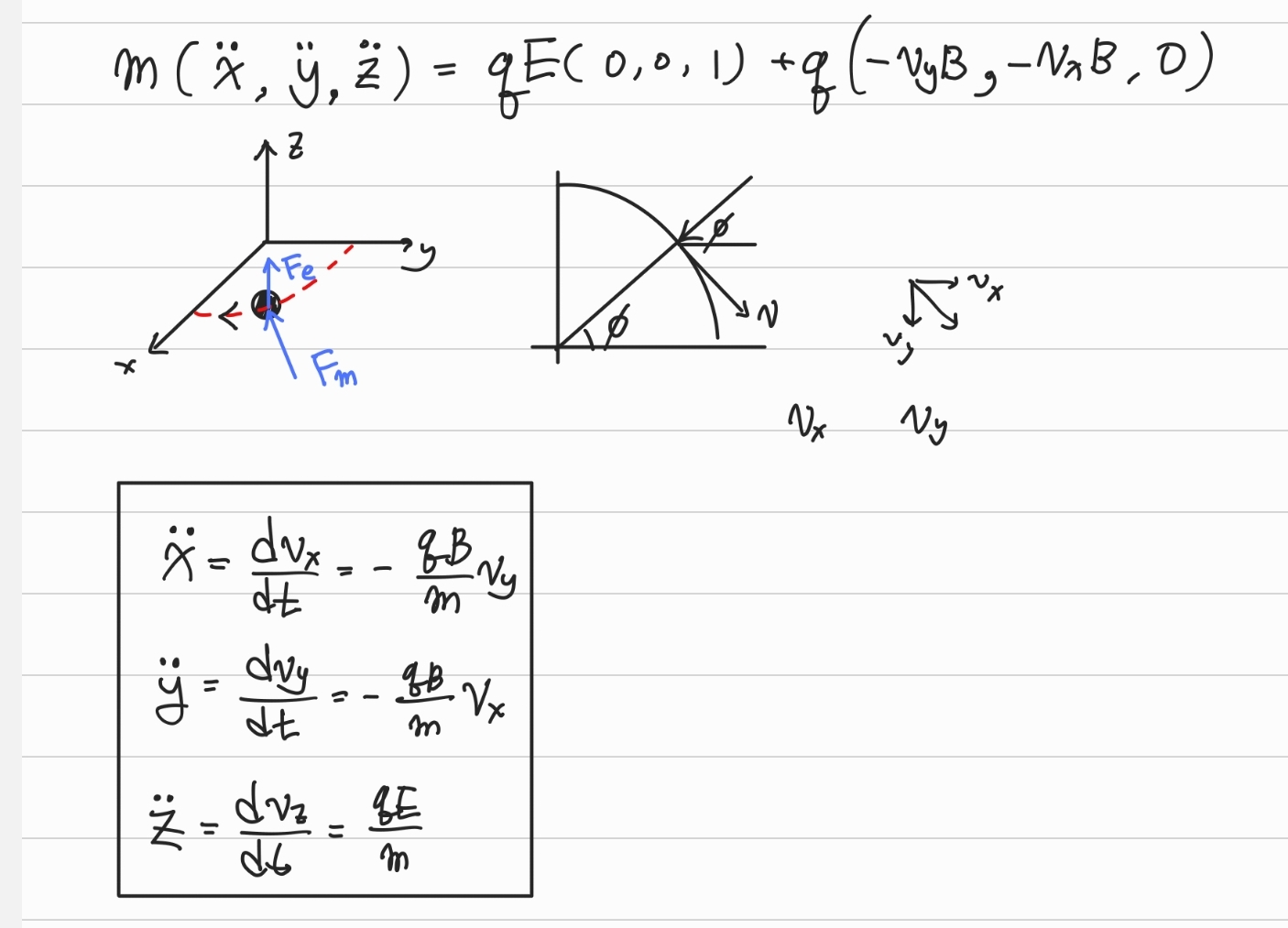
• 또한 $z$축에서의 시간에 따른 속도는..
  

• 최종적으로 모든 속도를 시간에 따라 적분해주면 다음과 같이 위치에 대한 함수를 구할 수 있다.

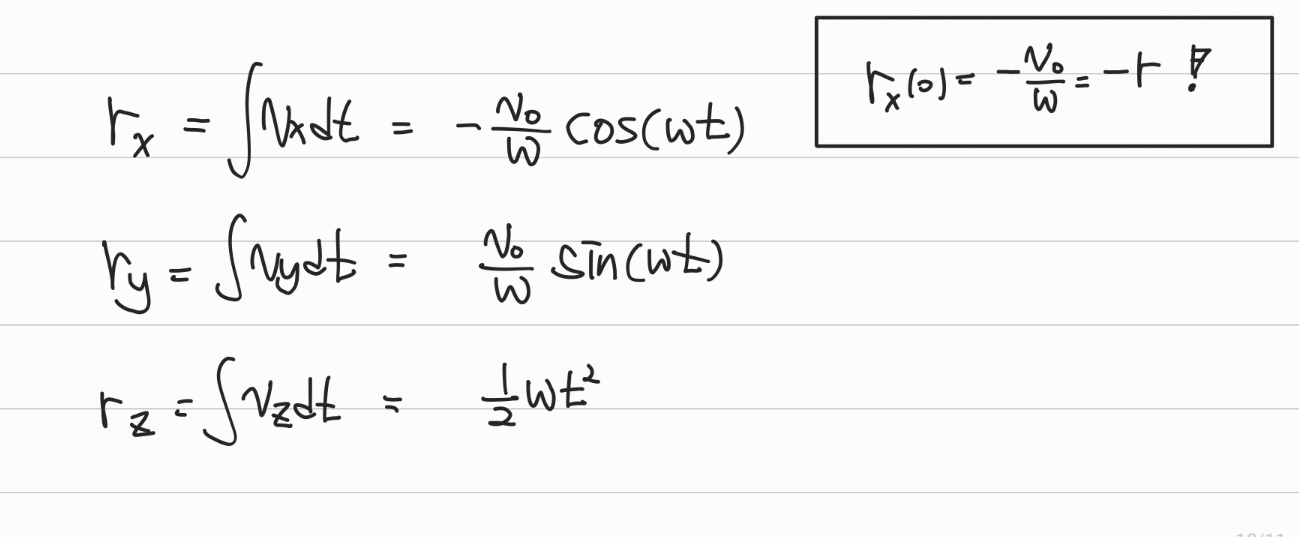
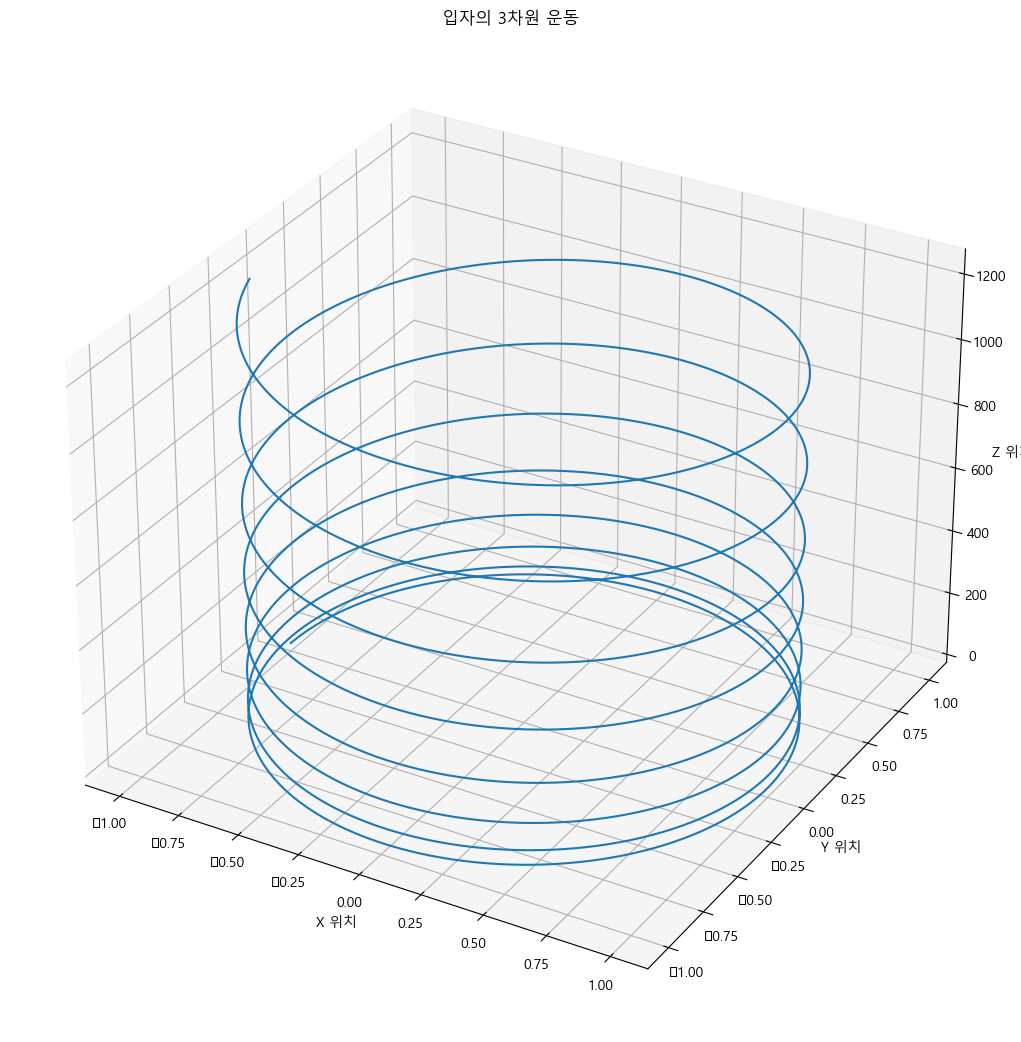
파이썬으로 양전하의 움직임에 대한 3차원 그래프를 그려보면 다음과 같다.