정전기장 3-10 Capacitor, Capacitance

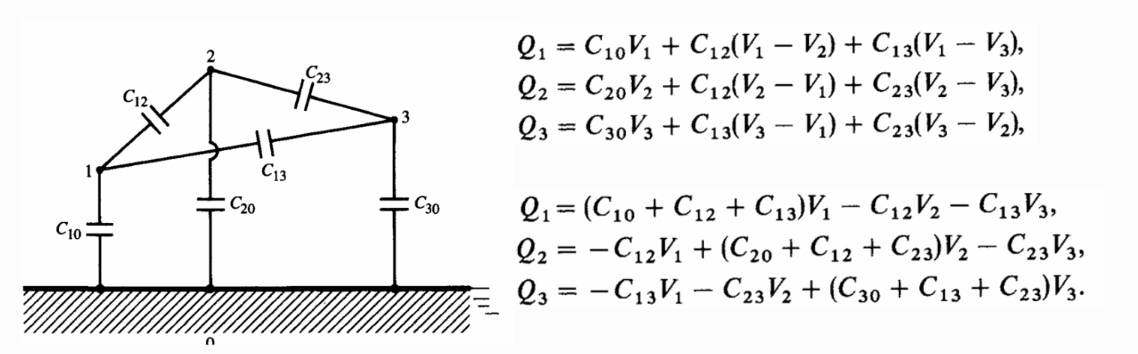
캐퍼시터와 정전용량

• 캐퍼시터는 전자부품에 해당한다. 전자회로에서도 중요한 요소에 해당하는데, 전기를 일시적으로 담아두고 방출도 가능한 소자이다.

캐퍼시터 문제를 푸는 방법은 두 가지가 있는데, 방법 2인 전압을 먼저 가정하는 방법은 경계조건을 이용한 문제풀이로 4장에서 한다.

• 
• Capacitance(정전용량)은 Q와 V에 무관한 시스템의 특성이다.
  따라서 어떤 Q나 V를 고정시키고 이떄의 V나 Q를 측정하면 C를 구할 수 있다.
• 

• 예제 3-17
  

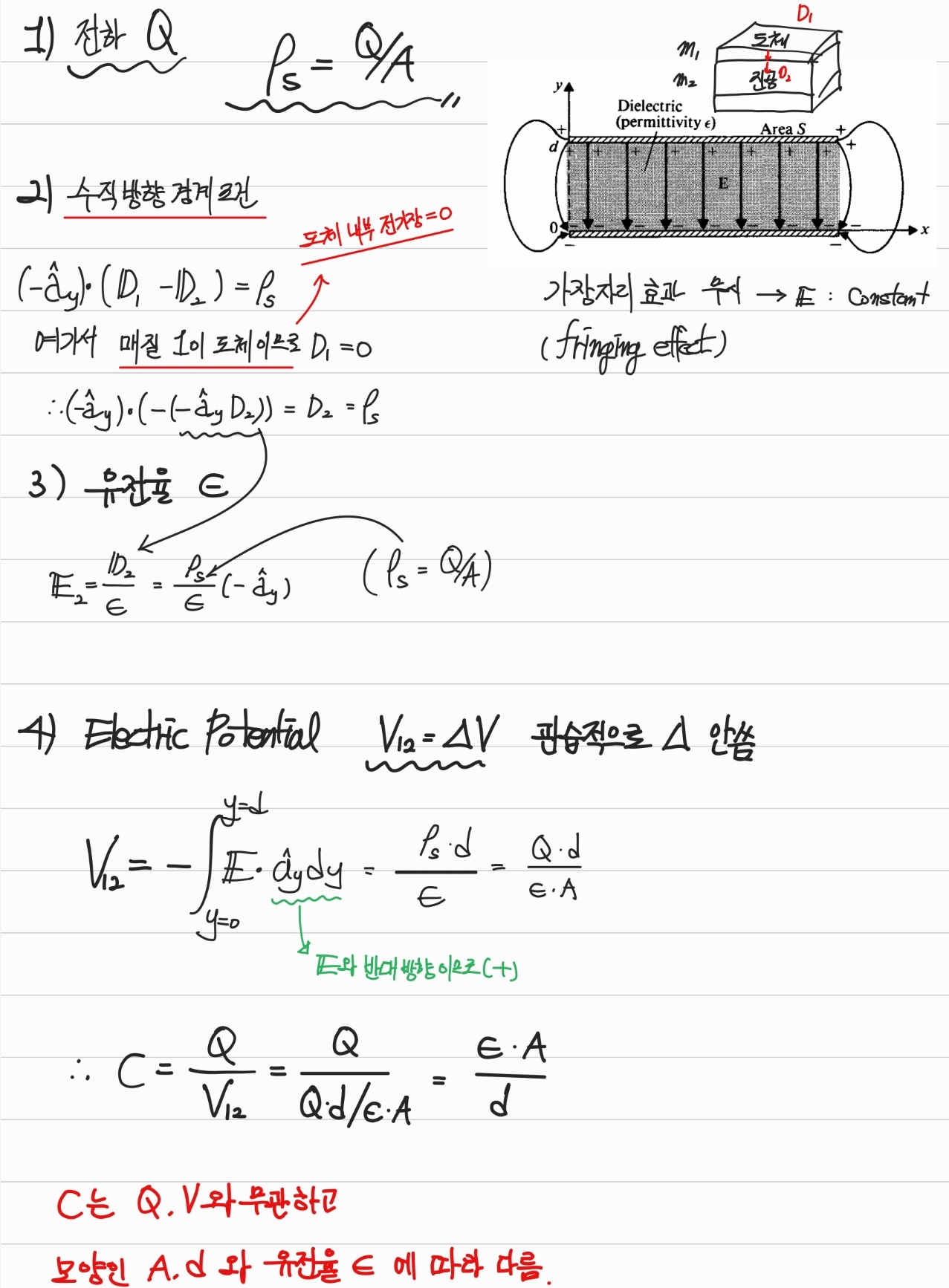
• 예제 3-18
  

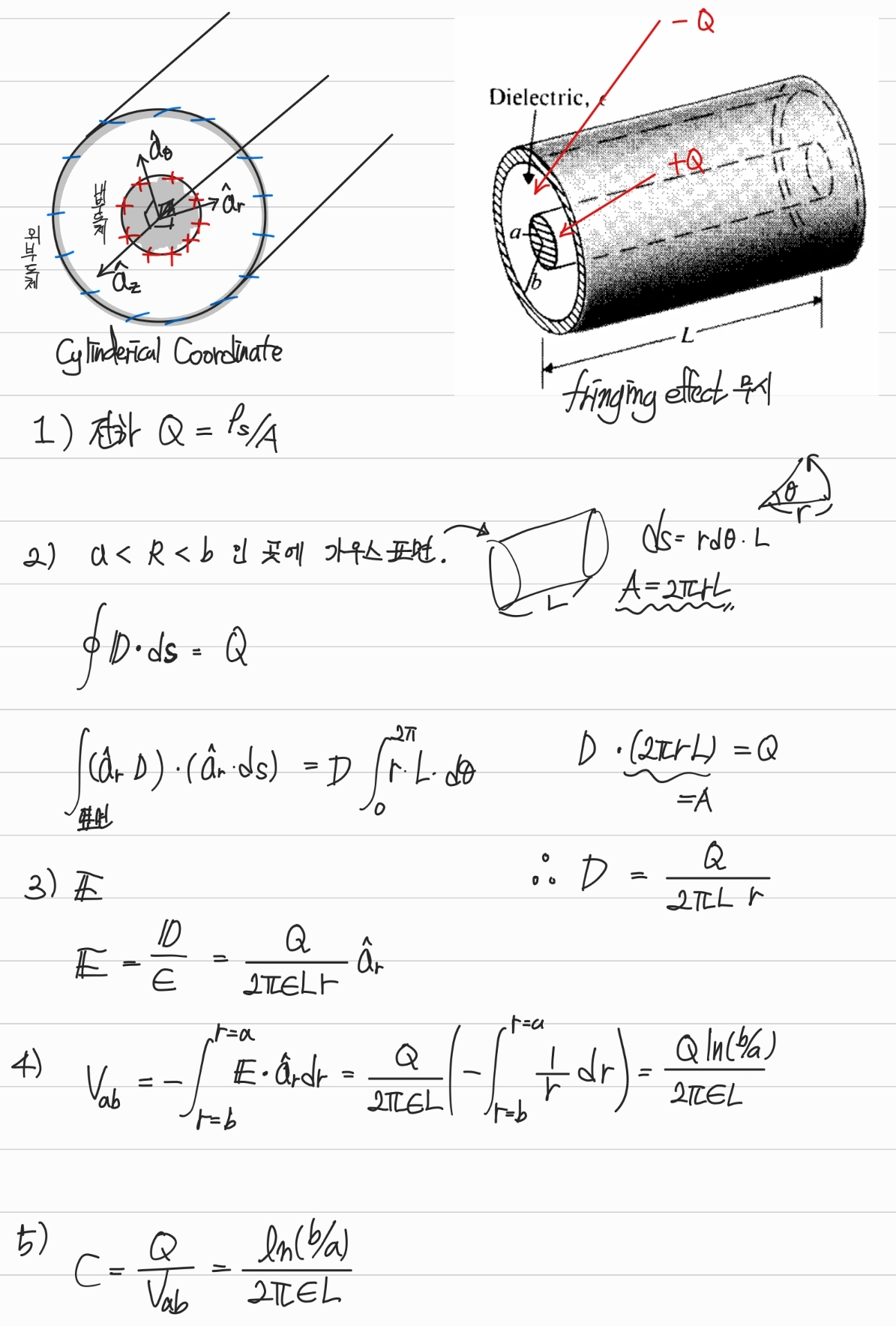
• 두 도체 사이의 전기장이 일정하지 않기 때문에 V에서부터 E와 Q를 풀어내는 것이 어렵다는데 아직 이것이 의미하는 바를 모르겠다.

• $\mathbf{E}=-\nabla V$ 에서 $\mathbf{E}$가 $\mathbf{r}$의 함수가 되어서 포텐셜을 구하기 힘들어서 라는 생각만 해본다.

캐퍼시터의 직렬 및 병렬 연결

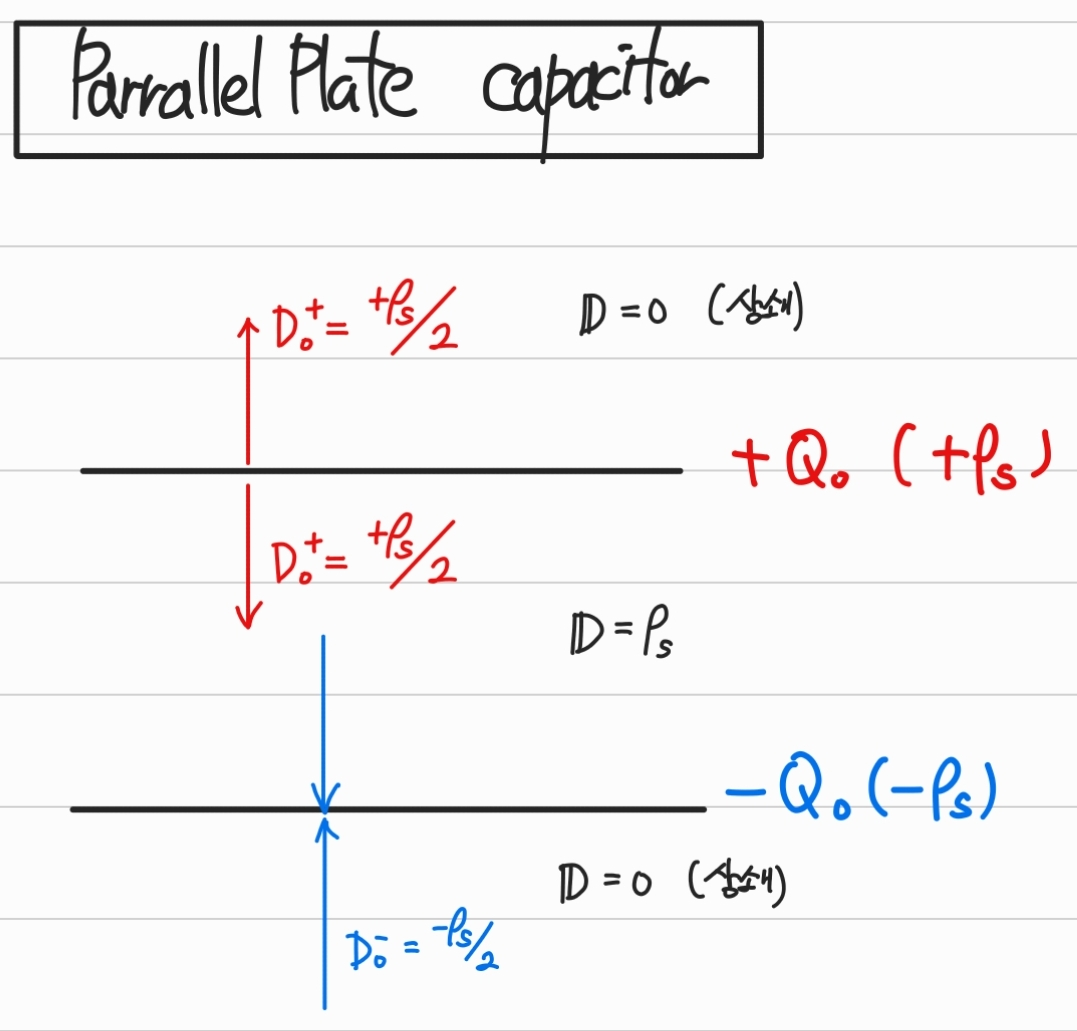
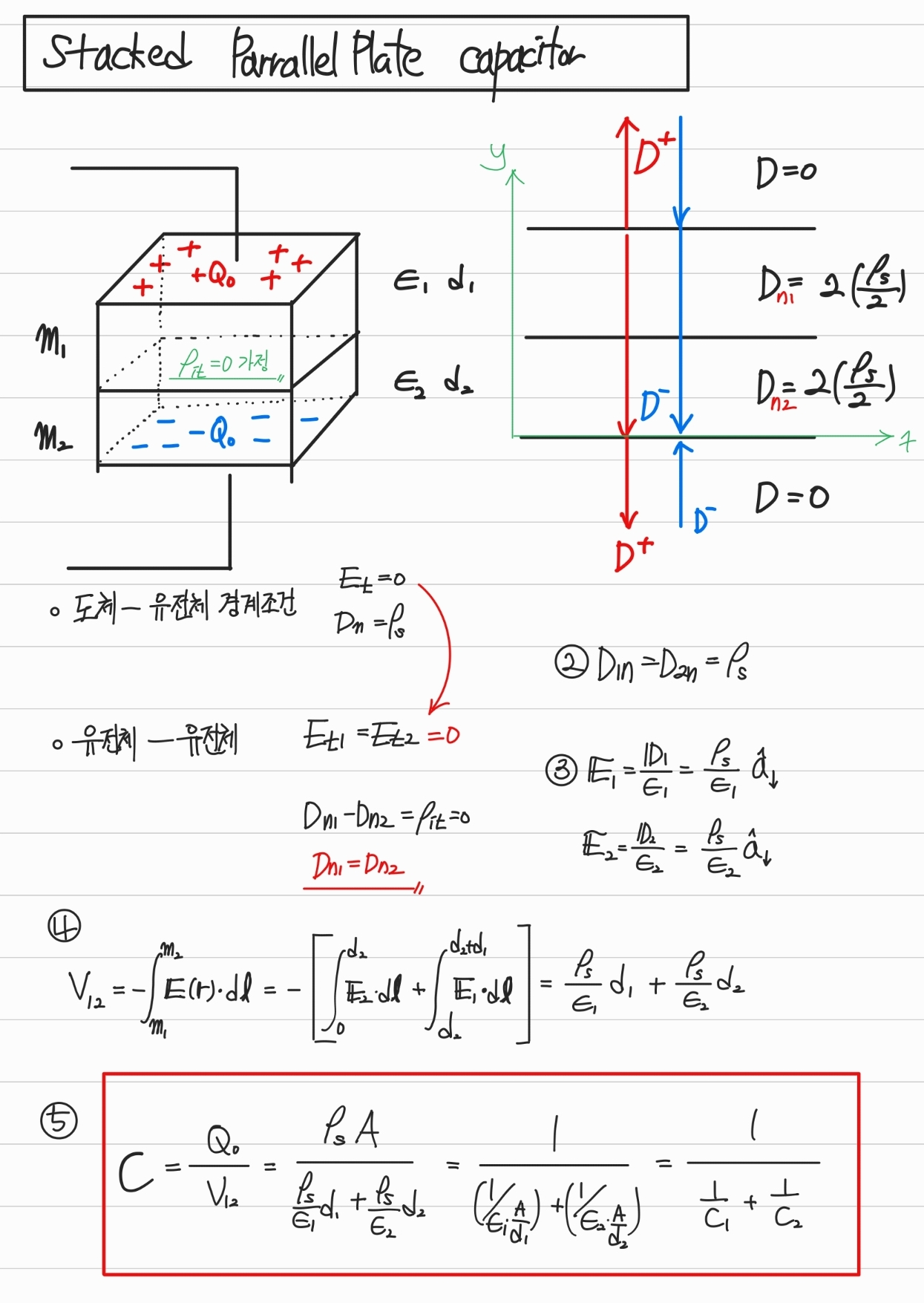
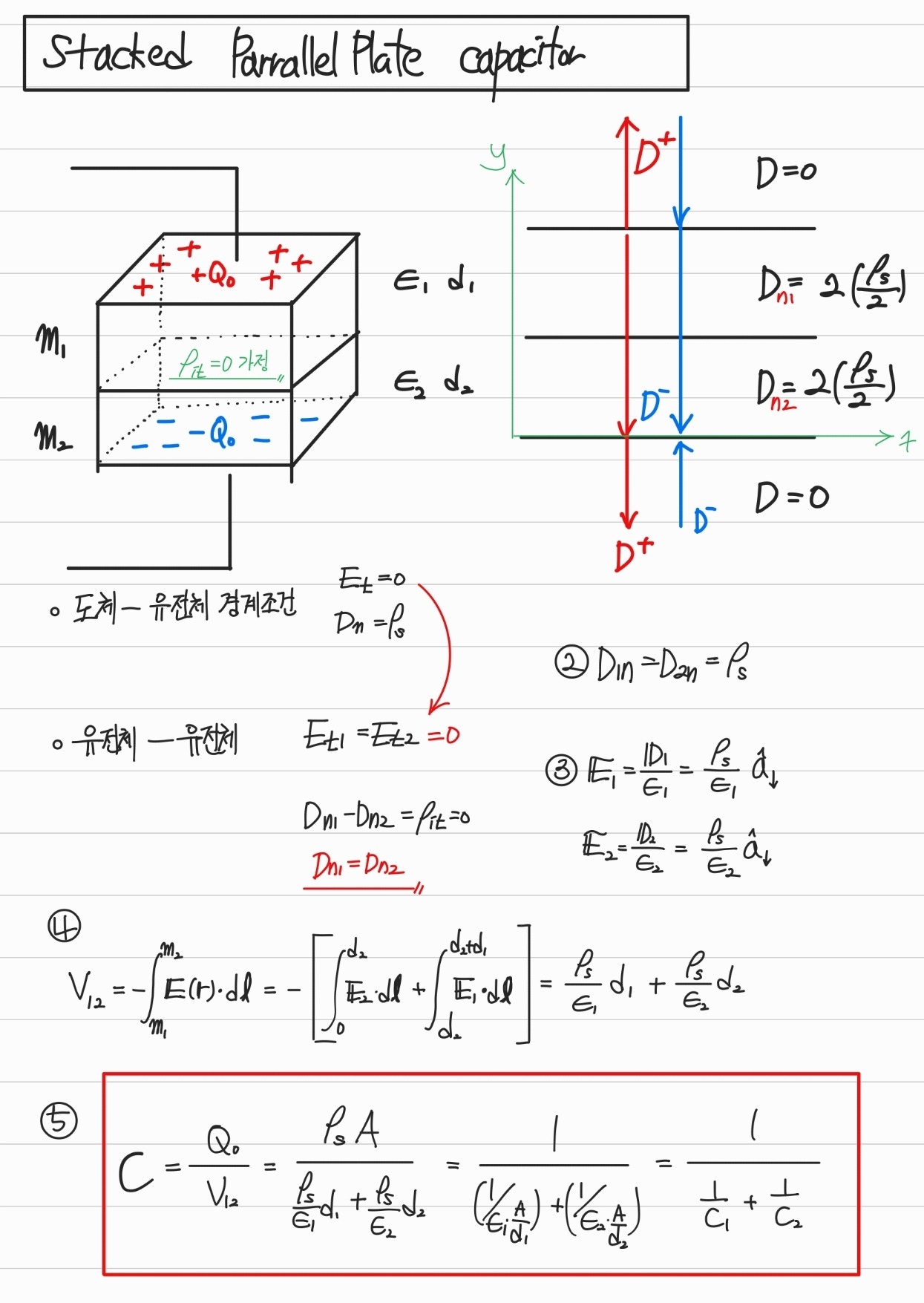
줄서있는 평판의 해답은 다음과 같은 결과를 가진다.

$\frac{1}{C_{sr}}=\frac{1}{C_1}+\frac{1}{C_2}$

• $C_{series}$ : 직렬에서 등가 정전용량

사실 회로이론을 수강해서 위의 식을 알고있었지만, 이런 이유인지는 모르고 그냥 암기했던 것 같은데 가려운 것을 긁은 기분이다.

$C_{sr}=\frac{C_1C_2}{C_1+C_2}=\frac{C_1}{1+\frac{C_1}{C_2}}$

• $C_1$을 정전용량이 작은 값이라고 하면 등가 정전용량은 두 정전용량 중 작은 값보다 작다는 것을 알 수 있다. $\frac{C_1}{C_2} <1$이 되기 때문이다.

• 직렬로 구성된 Capacitor System을 구성하게 될 경우에 이런 사실을 알아두면 유용할 것이다.

캐퍼시터가 병렬로 연결된 경우는 생각하기 쉽다.

외부 단자가 모두 캐퍼시터에 연결되어 있기 때문에 단자에 전압이 인가되면 양단에 전하가 축적될 것이다.

• $Q=Q_1+Q_2+\dots+Q_n$

이므로

• $C_{||}=C_1+C_2+\dots+C_n$

이다.

다중도체 시스템에서의 정전용량

• 그냥 넘어가려고 했지만 아주 간단하게만 다룸.

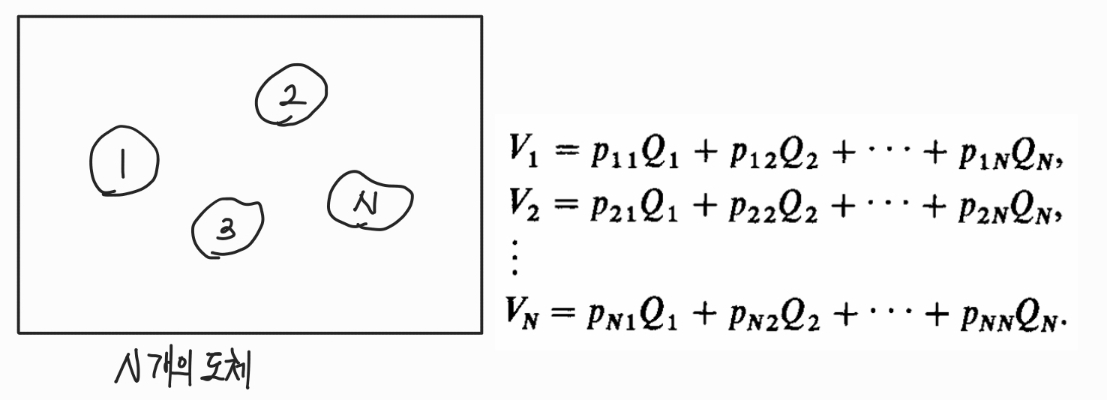
• N개의 도체가 존재하는 시스템에서 어떤 도체에 존재하는 전하는 다른 도체에 영향을 미칠 수도 있을 것이다.

• V와 Q는 선형 관계에 있고 다음과 같은 선형 연립방정식을 만족시킨다.

• 도체만 존재한다고 했으므로 총 전하량은 0이다.

정리하면 다음과 같은 식을 만족한다. 간단하게 3개만 나타냄.

$c_{ij}$는 정전용량계수이고, 다른 모든 도체가 접지되어 있을 때의 전하와 전압의 비율이다.

내용이 더 있지만, 주목해야 할 점으로 뽑은 것은 도체들이 여러 개 있을 경우 서로 상호작용하여 복잡해 진다는 것이다.

정전기 차폐

• 도체 간의 간섭을 줄이기 위해 사용하는 기법이다.

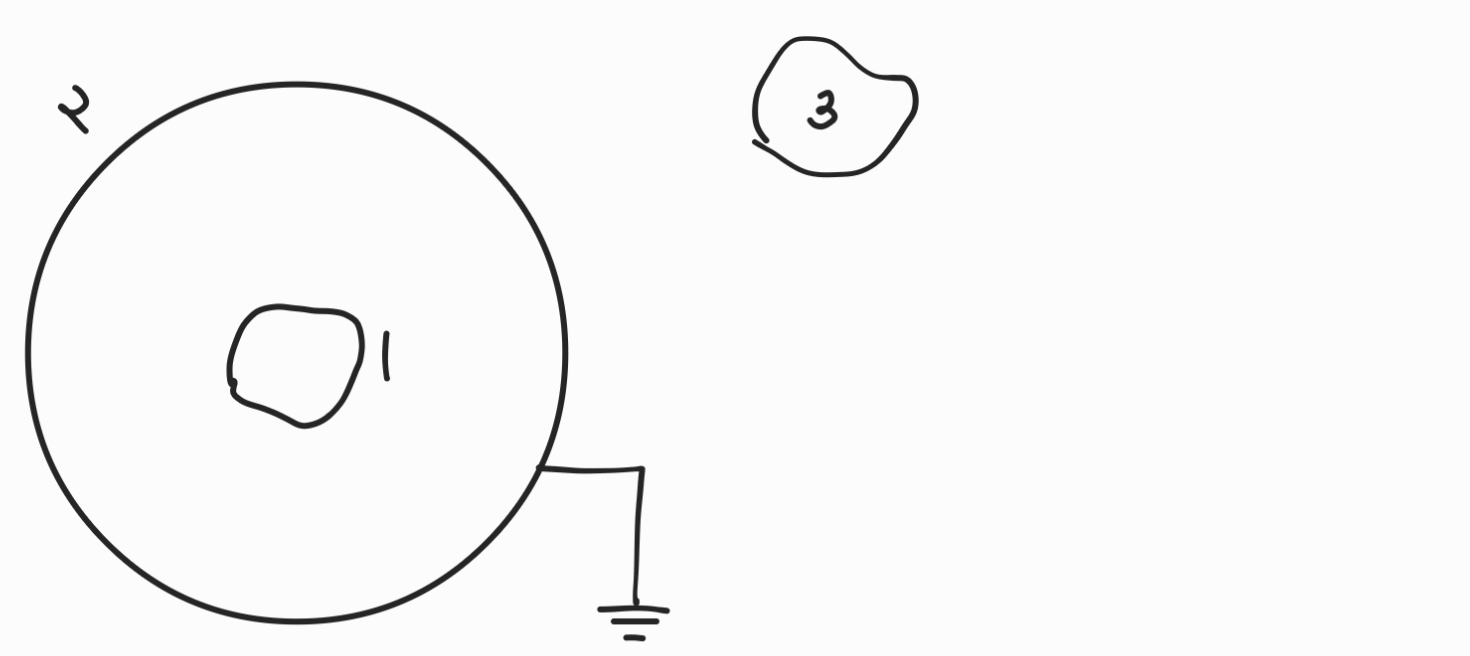
다음과 같이 2번 도체껍질이 접지된 경우를 보면,

• $Q_1=C_{10}V_1+C_{12}V_2+C_{13}(V_1-V_3)$
  에서

• $V_2=0$으로 기준점을 잡을 수 있다.(Ground)

• 그런데 도체껍질내부 $\mathbf{E}=0$이므로 내부에 전위차는 존재하지 않고 $V_1$또한 $0$이다.

• 따라서 $C_{13}$은 $Q_1=0$이면 $V_3$에 관계 없이 $0$이여야 한다.

결론 :따라서 $C_{13}$은 $Q_1=0$이면 $V_3$에 관계 없이 $0$이여야 한다.

$V_3$가 $Q_1$에 영향을 못 미치고 도체1과 3은 서로 전기적으로 차폐되었다고 한다.

이해가 안될 경우 참고 그림