- 쿨롱 법칙
- 가우스의 법칙과 응용
>무한 자유공간에 점전하가 정지되어 있는 경우
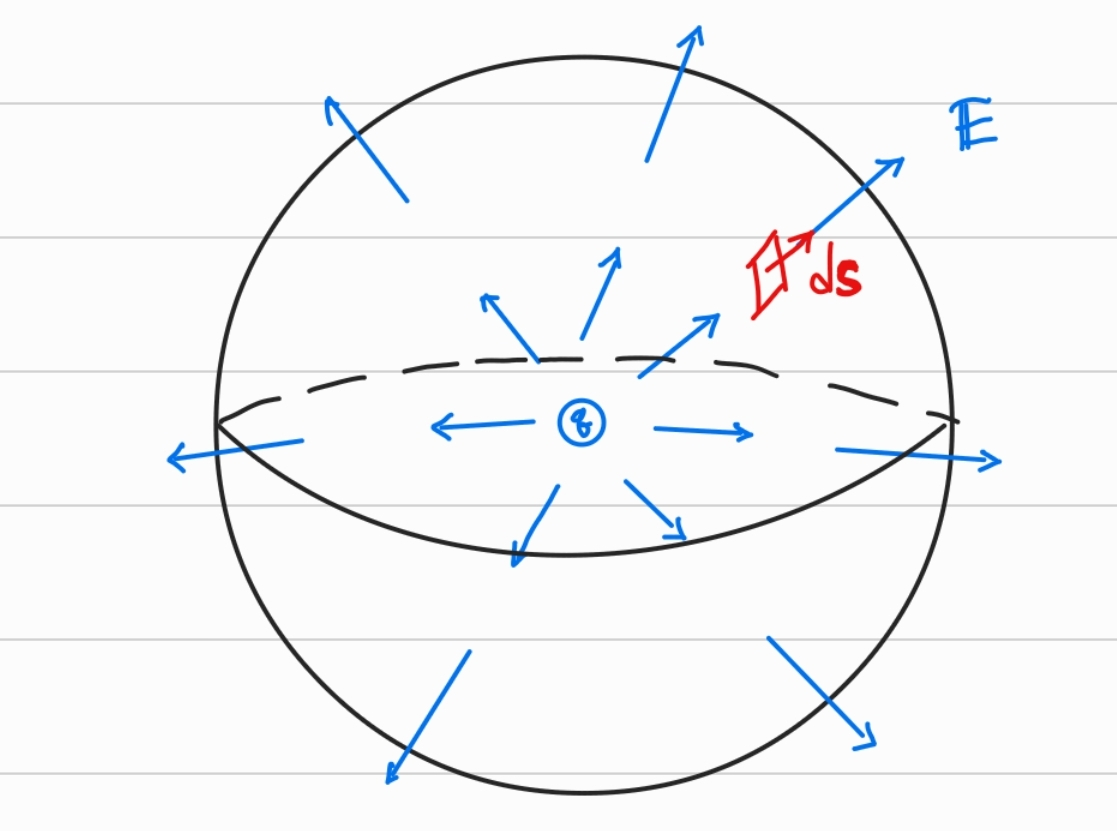
반지름이 R인 가상의 구면을 생각해 본다.
점전하 구조는 방향성이 없기 때문에 가상의 구면상에서 모든 위치에서 같은 크기의 값이 방사형으로 분포할 것이다.
(A point charge has no prefered direction : symmetry)
와 의 방향이 같기 때문에 다음과 같다.
(구의 겉넓이, 구좌표계로 적분해보면 금방 나옴, hint: ds=sindd)
임의의 공간좌표 P의 위치벡터가 이라고 하면,
쿨롱의 법칙
[V/m]
위치벡터를 풀어서 분모에 세제곱으로 사용함.
Convention
prime: Source Point
prime x: Field Point
The Principle of Superposition
이산 전하그룹에 의한 전기장
임의의 지점에서 총 전기장 의 크기는 각각의 독립된 전하에 의해서 발생되는 전기장의 크기의 벡터의 합과 같다
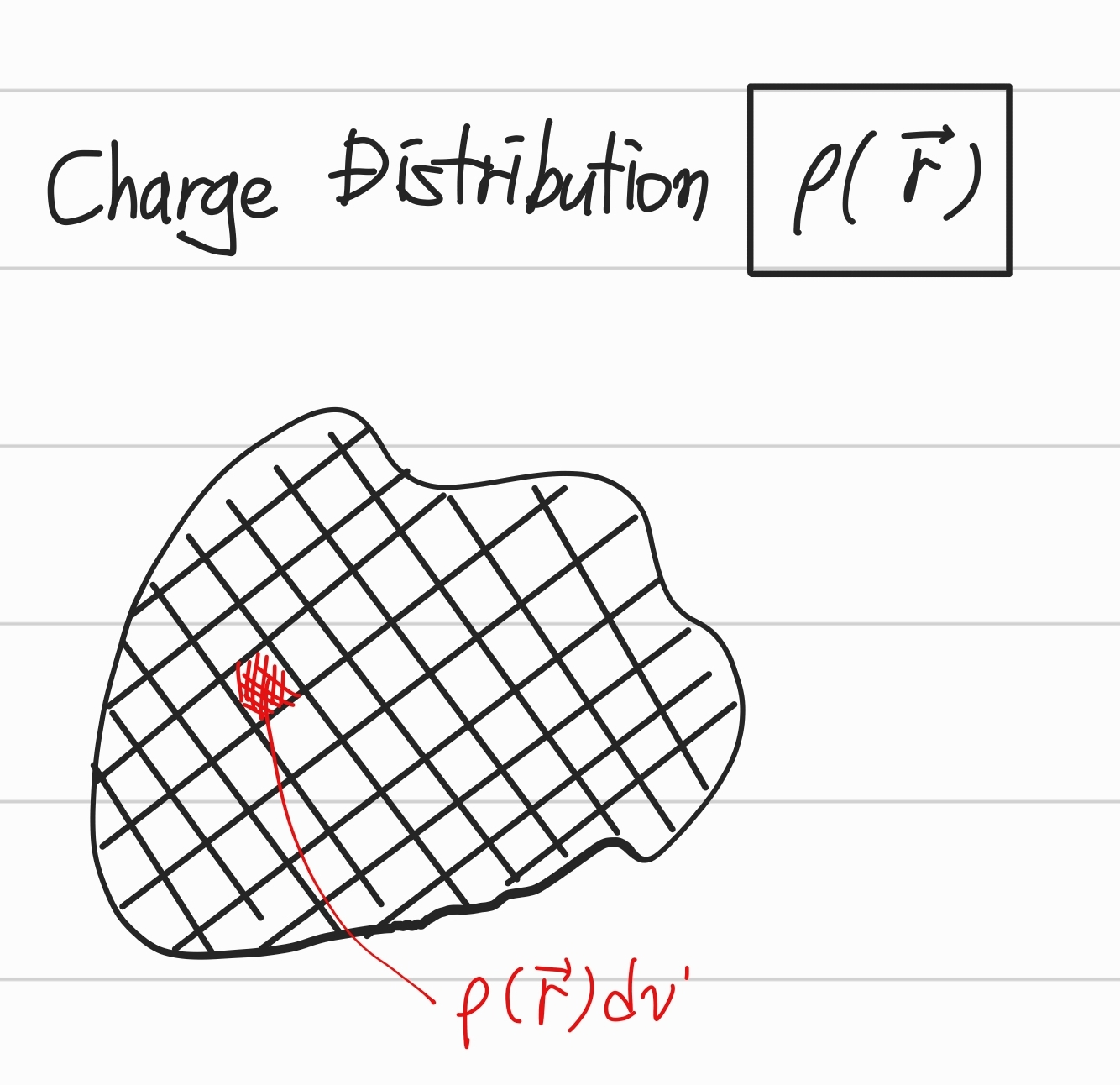
연속적인 전하 분포에 의한 전기장
Electric Field due to a continuous charge distribution
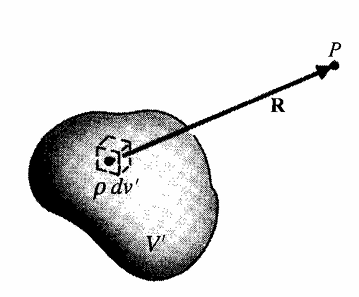
각 미소 전하는 점전하로 간주할 수 있고 전하는 공간 좌표의 함수이다.
미소 공간에 의한 P에서의 전기장의 세기를 구할 수 있다.
미소 체적에 대한 경우 :쿨롱의 법칙
가우스의 법칙과 응용
가우스의 법칙은 임의의 폐곡면을 통해 방출되는 전기장 의 총 전속은 폐곡면 내부의 총 전하를 로 나눈것과 같다.
여기서 면 S는 임의의 폐곡면이고 실제로 존재하지 않아도 된다.
전하 소스가 대칭 구조로 분포되어 있는 경우에 유용함.
-> 폐곡면에서의 전기장의 세기의 수직 성분이 상수값을 갖기 때문이다.
그렇게 되면 좌변을 구하기가 쉬워지고, 전기장의 세기의 값을 구하기 쉬워진다.
가우스의 법칙을 잘 활용할 수 있는 폐곡면은 다음과 같다.Gaussian Surface
- 전하 분포가 대칭 조건을 만족
- 주어진 전하 분포에 대응하여 의 수직 성분이 상수값이 되는 폐곡면
폐곡면에서의 전기장의 세기의 수직 성분이 상수값을 갖기 때문이라는 게 잘 이해가 안되는데 문제를 풀면서 살펴보겠다.
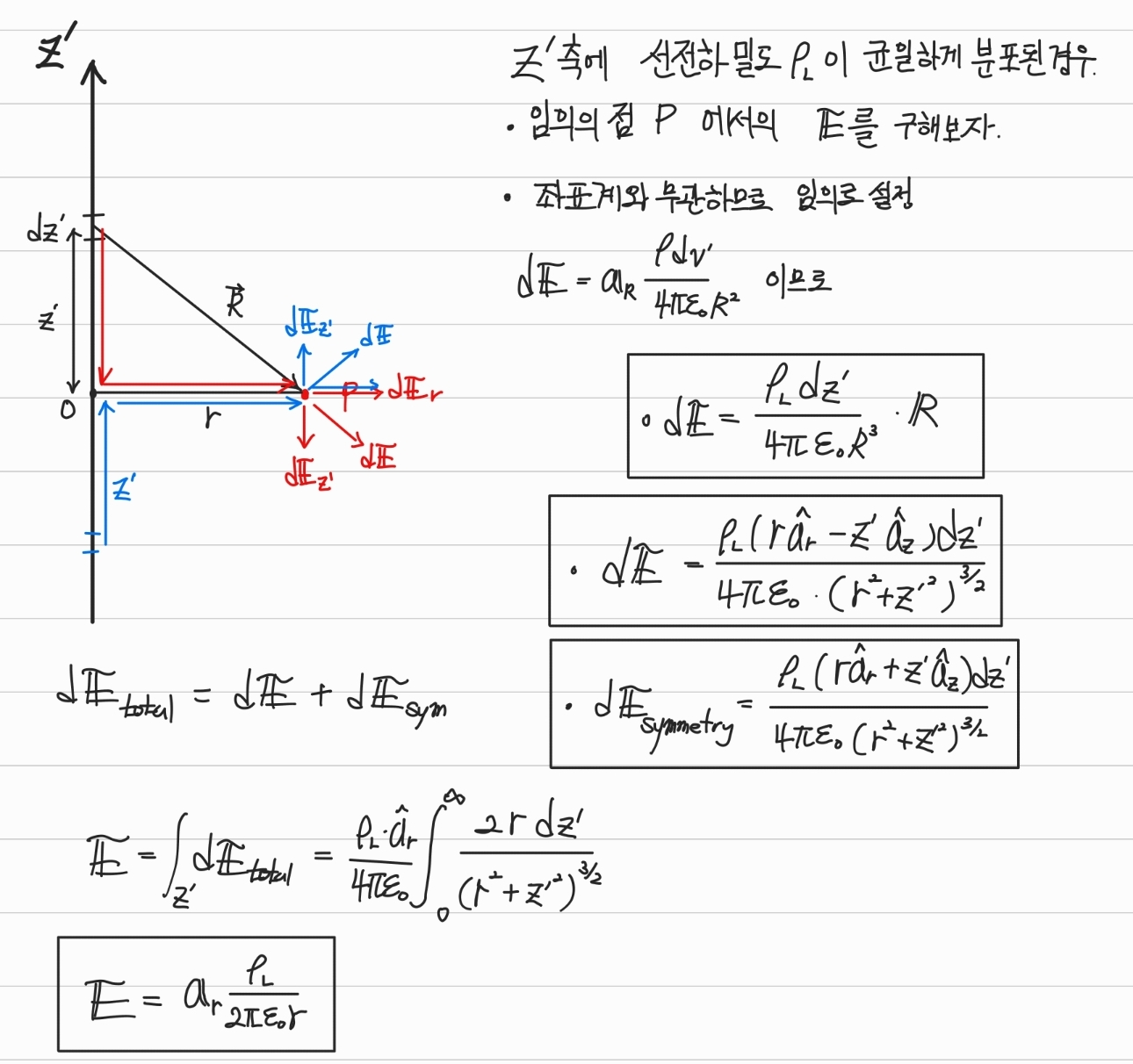
연속적인 전하분포에 의한 전기장(무한히 긴 직선 선전하 件)
- 임의의 점을 잡아서 구하기
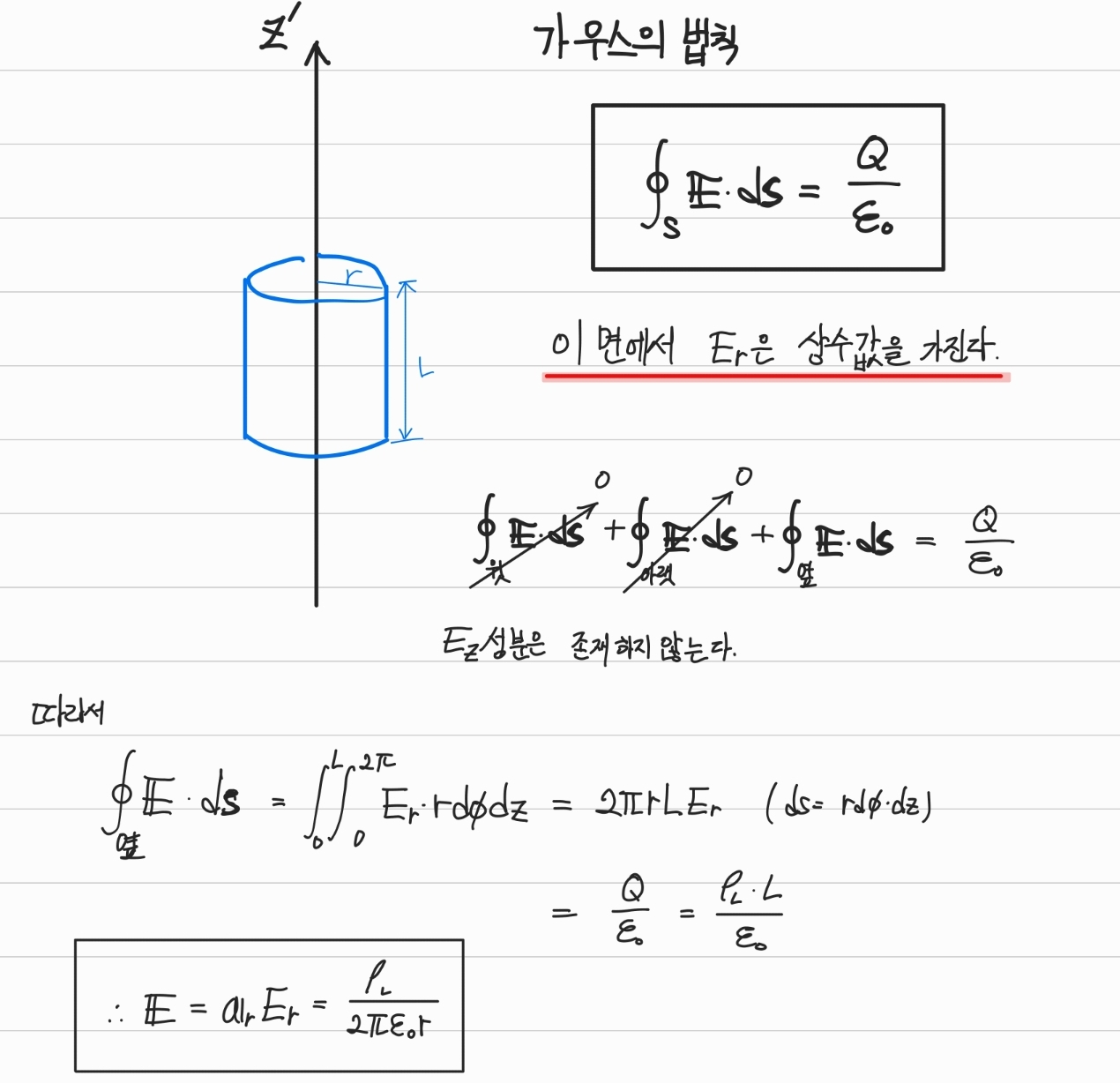
- Gaussian Surface를 정의하여 구하기
- 임의의 점에 대한 전기장의 세기
- Gaussian Surface를 정의하여 구하기
위의 문제에서 봤듯이 는 성분은 사라지고 선전하에 대해 수직 성분으로만 존재한다.
따라서 다음과 같이 Gaussian Surface를 구성한다.
예제 3-2
- 쿨롱의 법칙이 성립한다는 것과 다음은 동치이다.
어떤 전하가 균등하게 분포된 도체 껍질 내의 시험전하가 느끼는 전기장의 세기는 이다.
이 투고에서 쿨롱의 법칙에서 두 전하 간 작용하는 힘은 거리의 제곱에 반비례 하는 지 안 하는 지 실험으로 엄밀하게 알 수 없다고 했지만, Cavendish, Maxwell, William등의 실험으로 증명됨.
Inverse Square Law가 성립하지 않는다면 P의 위치에 이 될 수 없었을 것이다.
- 총 전하량 Q가 반지름 b인 얇은 구 도체껍질에 고르게 본포되어 있다. 얇은 도체껍질 내부의 임의의 지점에서 전기장 세기를 구하라.
첫 번째 접근방식: 구 내부의 빈 공간에 임의의 점 P를 잡고 Gauss's Law를 적용할 수 있는 Gaussian Surface를 그려본다.
-> 도체 내부에는 전하가 존재하지 않기 때문에 임을 바로 알 수 있다.두 번째 접근방식: 점 P를 꼭지점으로 하고 입체각이 인 두 개의 원뿔을 그리고 각 면적을 라고 한다.
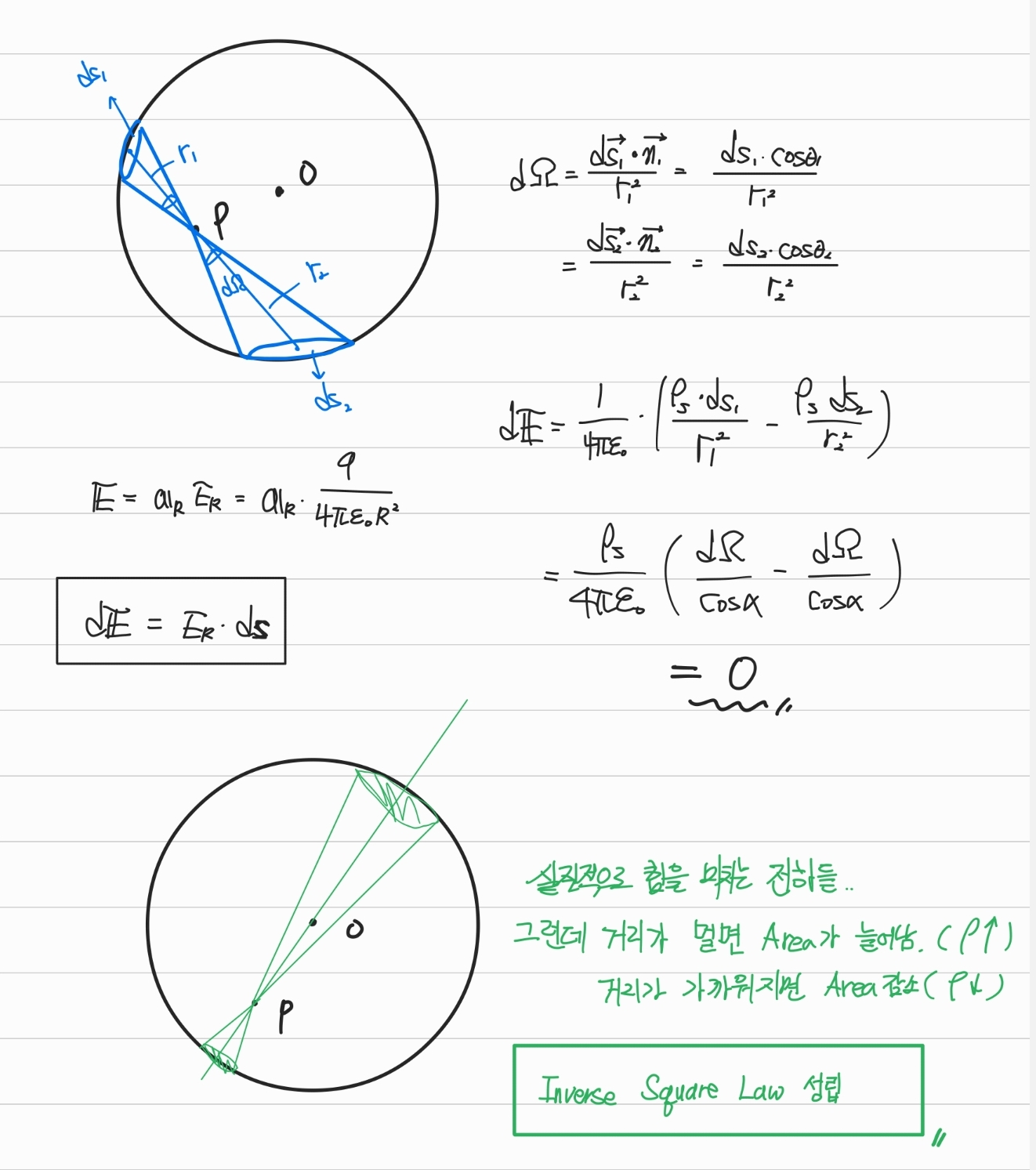
- d; Solid Angle 이란?
만약 Gauss's Law를 사용하지 않는다면, 1) 모든 전하분포를 미소 체적 전하로 나누고, 2) 임의의 지점까지의 을 구한 다면 3) 삼중적분을 수행하여야 한다. 전하 분포가 대칭청을 갖춘다면, Gauss's Law를 사용함이 바람직하다.