정전기장 3-5 전위

Definition of Electric Potential V

Potential Energy는 일(Work)와 관련되어 있다.

지금 일을 하고 있지는 않지만 일을 할 수 있는 능력에 관한 내용이다.

---

---

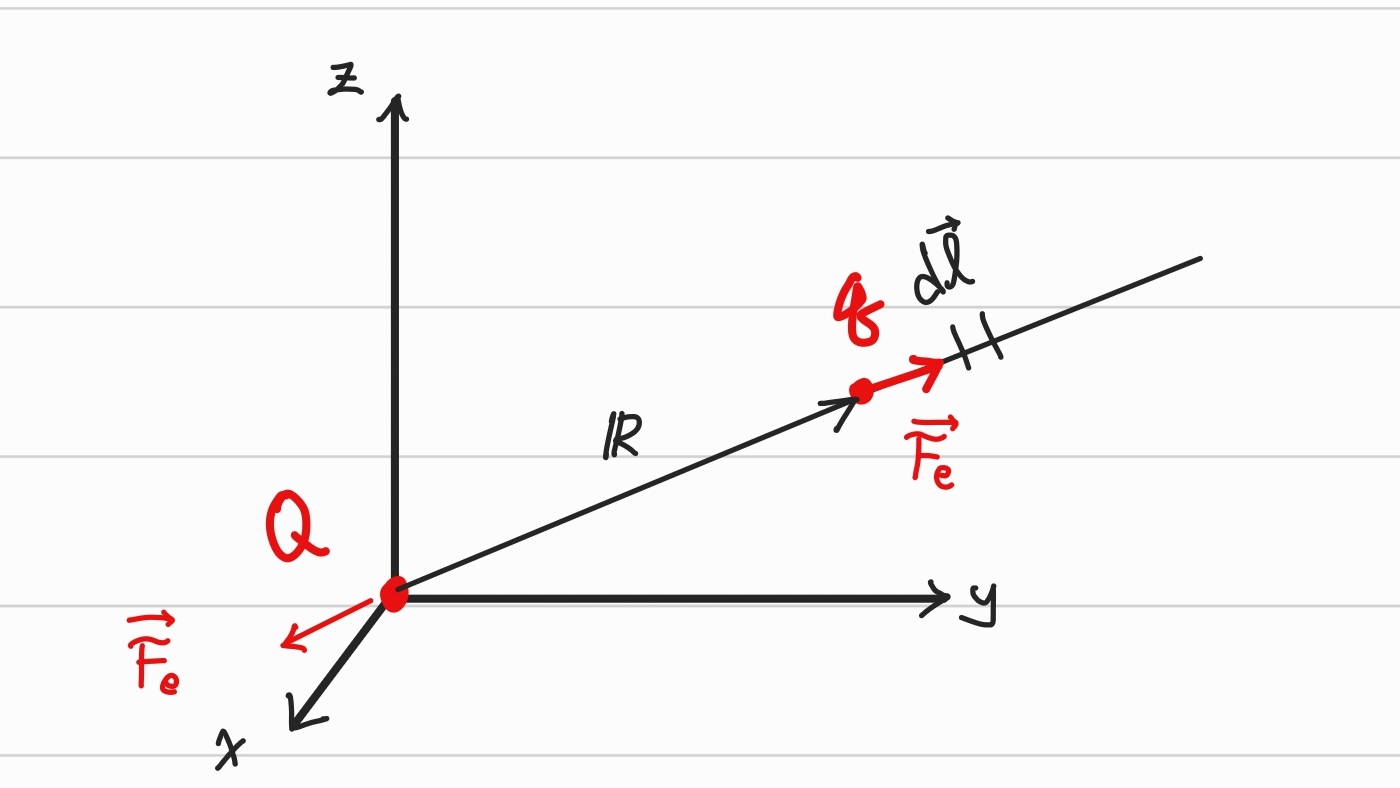
위 그림을 반대로 생각하면,

역학적 에너지 보존 법칙에 따르면, 외부와의 에너지 교환은 없고 내부에너지의 변화는 없다.

• $E_{total}=U_{potential}+KE =Constant$
  
  

• 전하가 $\vec{r}=\vec{r}_2$에서 $\vec{r}=\vec{r}_1$ 로 위치를 변경할 때
  Net Kinetic Energy Change가 없다고 하면
  보존력인 정전기력이 전하에 해준일(work done to a charge)은
  $Potential Energy$의 변화와 같다. 따라서,
  
  

$W=\int\vec{F}\cdot d\vec{r}=\int q\vec{E} \cdot d\vec{r}=\frac{Qq}{4\pi\epsilon_0r}=U_2-U_1$

$\Delta U=W=\frac{Qq}{4\pi\epsilon_0r}$ 이다.

Potential Energy의 차이를 단위전하당으로 바꾸면,

$V_2-V_1=\Delta V=\frac{\Delta U}{q}=\frac{Q}{4\pi\epsilon_0r}$

Scalar Potential V

$V=\frac{Q}{4\pi\epsilon_0r}$ 이고, 종종 Delta를 생략한다

*************************************************************************

• 어떤 보존력 $\mathbf{F}$에 대해 다음 식이 만족하므로
  $\mathbf{F}=-\nabla U$
  전기장의 세기
  $\mathbf{F}=q\mathbf{E}$
  의 식을 이용하여
  $\frac{\mathbf{F}}{q}=\frac{-\nabla U}{q}$
  
  
• $\mathbf{E}=-\nabla V$

위의 식은 단위 전하가 각 위치에 있을 때의 전위에너지 차이를 나타내는 것이다. 단위전하가 갖고 있는 에너지 V를 전위라고 한다.

• 
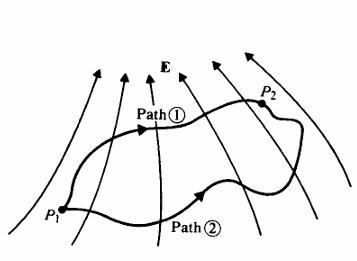
• 또한 경로와 무관하다는 것을 내포한다. 경로에 무관하지 않는다면 에너지의 이득이 발생할 수 있기 때문이다.

이렇게 두 점사이의 전위차(정전기장 전압)을 정의한다.

• 전위에 관해 절대적인 값을 정의할 수 없다. 기준점에 대한 상대값을 정의한 것이다.
• $\mathbf{E}$의 방향을 거슬러 이동할 때 전위 $V$가 증가하기 때문에 부호가 다른 것이다.
• $\nabla{V}$의 벡터 방향은 전위의 스칼라 값이 상수인 점들로 형성된 면에 대해 항상 법선 방향이다. 따라서 $\mathbf{E}$는 등전위면(equipotential surfaces)에 항상 수직이다.

전하 분포에 의한 전위

구면 위의 경로적분을 수행하면

$\mathbf{F}$는 주어지는 거리 적분 변수에 수직이므로 $P_1$ 에서 $P_3$ 구간 동안에 소모되는 일의 크기는 $0$ 이다.

전하가 주어진 영역에 연속적으로 분포된 경우에는 전체 영역에 대해 적분하여 전위를 구한다.

전기장의 세기의 경우와 동일함.

$\mathbf{V}=\frac{1}{4\pi\epsilon_0}\int_{V'}\frac{\rho}{R}dv'$

가우스의 법칙이 적용되기 어려운 조건에서 $\mathbf{E}$를 직접적으로 구하는 방법을 예제를 통해 알아보자.

판은 원대칭 구조이지만, $\mathbf{E}$의 수직성분이 일정한 상수가 되는 폐곡면이 존재하지 않는다.

• 예제 3-9 원판의 중심축상에 있는 임의의 지점에서의 전기장 세기를 구하라.

  
  

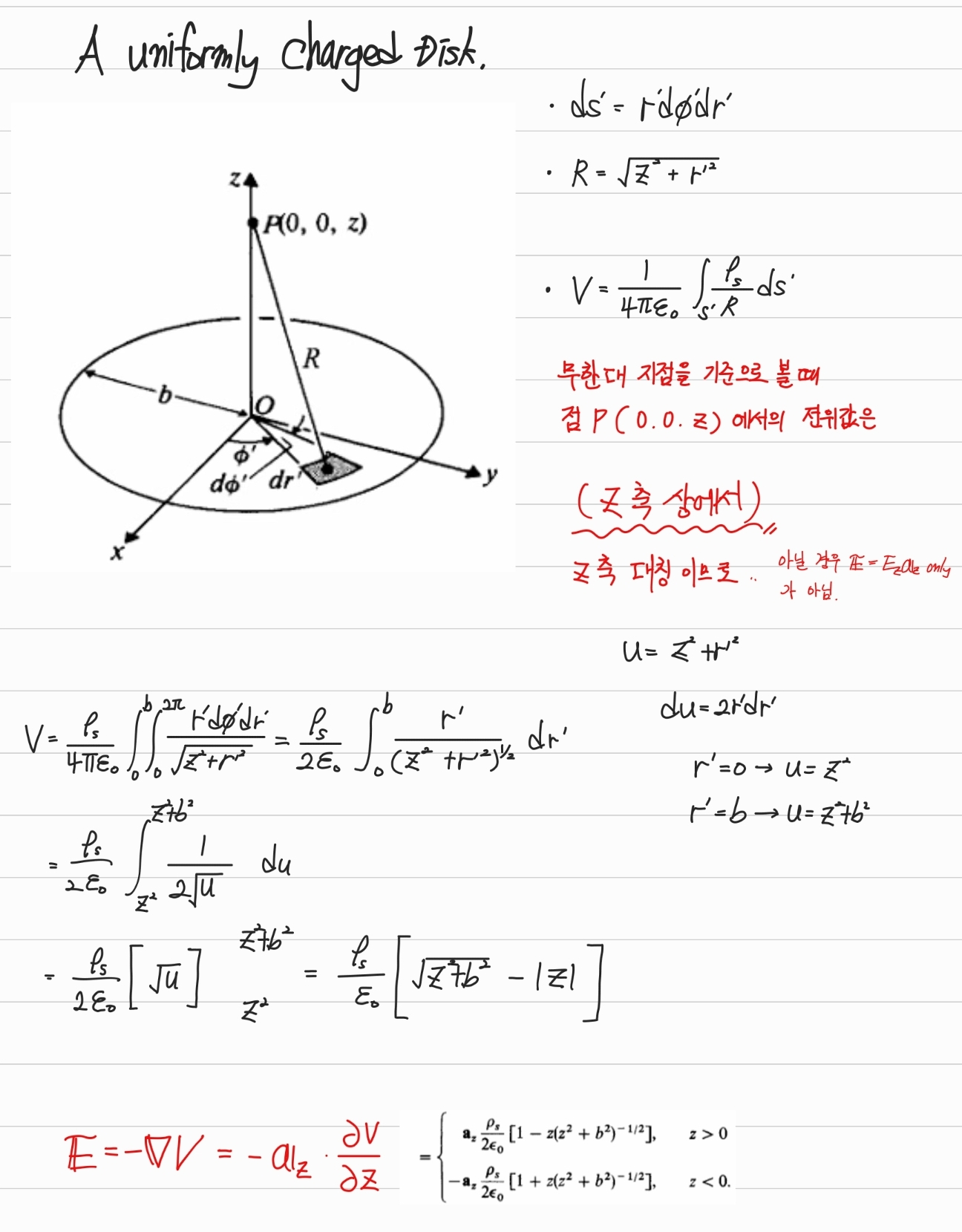
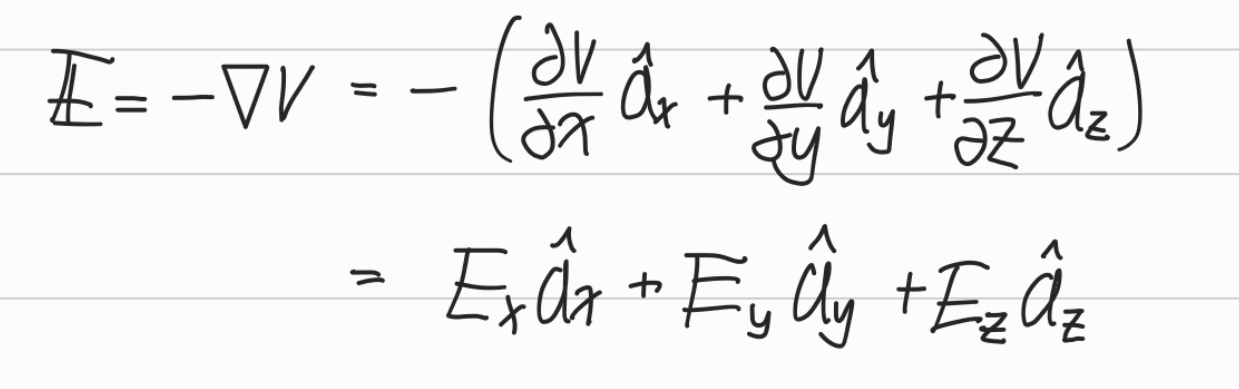
• 무한 면전하로의 근사도 가능하다.