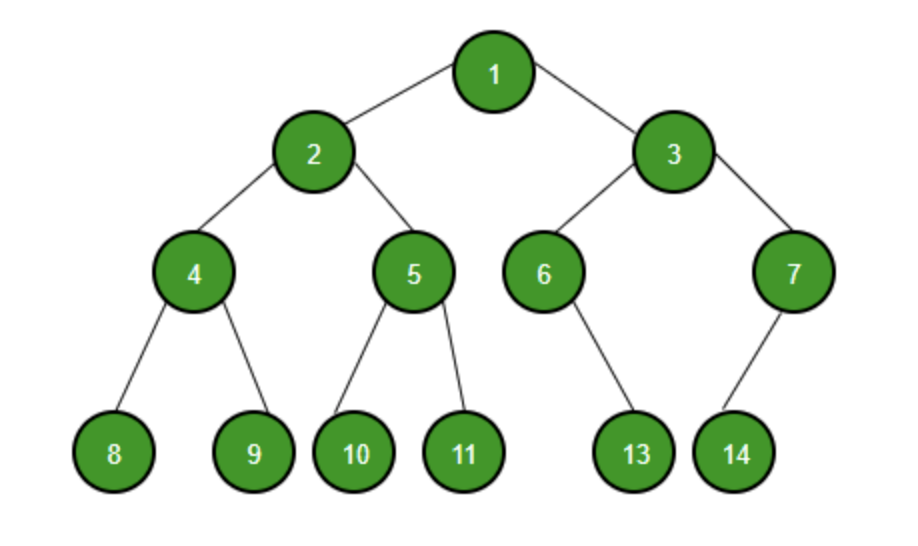
트리란?
-
값을 갖는 노드 간에 간선으로 연결된 계층적 자료구조
-
모든 노드는 0개 이상의 자식 노드를 갖고있으며, 부모-자식 관계라 부름
-
노드 개수가 N개이면 간선은 N-1개.
-
사이클은 존재하지 않으며, 사이클이 존재하면 그래프가 된다.
-
한 노드에서 다른 노드로 가는 유일한 경로는 하나이다.
트리 순회
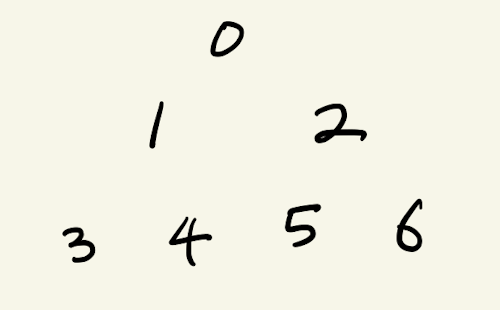
1. 전위순회(Pre-Order)
루트를 가장 먼저 방문. 루트->왼쪽->오른쪽
0 - 1 - 3 - 4 - 2 - 5 - 6
2. 중위순회(In-Order)
루트를 중간에 방문. 왼쪽->루트->오른쪽
3 - 1 - 4 - 0 - 5 - 2 - 6
3. 후위순회(Post-Order)
루트를 마지막에 방문. 왼쪽->오른쪽->루트
3 - 4 - 1 - 5 - 6 - 2 - 0
4. 레벨순회(Level-Order)
레벨 순서대로 방문
0 - 1 - 2 - 3 - 4 - 5 - 6
이진 트리 구현
TreeNode 클래스
public class TreeNode<T> {
private T data;
private TreeNode<T> parent;
private TreeNode<T> left;
private TreeNode<T> right;
TreeNode(T data) {
this.data = data;
this.parent = null;
this.left = null;
this.right = null;
}
TreeNode(T data, TreeNode<T> left, TreeNode<T> right) {
this.data = data;
this.parent = null;
this.left = left;
this.right = right;
}
TreeNode<T> setParent(TreeNode<T> parent){
this.parent = parent;
return this;
}
public T getData() {
return data;
}
public void setData(T data) {
this.data = data;
}
public TreeNode<T> getParent() {
return parent;
}
public TreeNode<T> getLeft() {
return left;
}
public void setLeft(TreeNode<T> left) {
this.left = left;
}
public TreeNode<T> getRight() {
return right;
}
public void setRight(TreeNode<T> right) {
this.right = right;
}
}- 변수 저장용 data, 부모 노드, 왼쪽 자식노드, 오른쪽 자식노드 저장
MyTree 클래스
import java.util.List;
public class MyTree<T> {
private TreeNode<T> root;
private int size;
public MyTree() {
}
public TreeNode<T> getRoot() {
return this.root;
}
public MyTree(TreeNode<T> root) {
this.root = root;
if(root != null) size = 1;
}
public int size() {return this.size;}
public void addLeft(TreeNode<T> now, T data) {
if(now.getLeft() != null) {
System.out.println("Left is full");
}
else {
TreeNode<T> child = new TreeNode(data);
now.setLeft(child);
child.setParent(now);
size+=1;
}
}
public void addRight(TreeNode<T> now, T data) {
if(now.getRight() != null) {
System.out.println("Right is full");
}
else {
TreeNode<T> child = new TreeNode(data);
now.setRight(child);
child.setParent(now);
size+=1;
}
}
public void delLeft(TreeNode<T> now) {
if(now.getLeft() == null) {
System.out.println("Left is empty");
}
else {
now.setLeft(null);
size-=1;
}
}
public void delRight(TreeNode<T> now) {
if(now.getRight() == null) {
System.out.println("Right is empty");
}
else {
now.setRight(null);
size-=1;
}
}
public void preOrder(TreeNode<T> node) {
//전위 순회. 루트를 맨 처음 방문 (중-왼-오)
if(node != null) {
System.out.print(node.getData() + " ");
if(node.getLeft() != null) preOrder(node.getLeft());
if(node.getRight() != null) preOrder(node.getRight());
}
}
public void inOrder(TreeNode<T> node) {
//중위 순회. 루트를 중간에 방문 (왼-중-오)
if(node != null) {
if(node.getLeft() != null) inOrder(node.getLeft());
System.out.print(node.getData() + " ");
if(node.getRight() != null) inOrder(node.getRight());
}
}
public void postOrder(TreeNode<T> node) {
//후위 순회. 루트를 마지막에 방문 (왼-오-중)
if(node != null) {
if(node.getLeft() != null) postOrder(node.getLeft());
if(node.getRight() != null) postOrder(node.getRight());
System.out.print(node.getData() + " ");
}
}
public static void main(String[] args) {
MyTree<Integer> myTree = new MyTree<>(new TreeNode(0));
TreeNode<Integer> root = myTree.getRoot();
myTree.addLeft(root, 1);
myTree.addRight(root, 2);
myTree.addLeft(root.getLeft(), 3);
myTree.addRight(root.getLeft(), 4);
myTree.addLeft(root.getRight(), 5);
myTree.addRight(root.getRight(), 6);
System.out.println("전위 순회");
myTree.preOrder(root);
System.out.println("\n중위 순회");
myTree.inOrder(root);
System.out.println("\n후위 순회");
myTree.postOrder(root);
}
}
-
root, size 갖음
-
TreeNode 객체로 root 노드 생성.
-
addLeft, addRight, delLeft, delRight 로 자식 추가 삭제 구현
-
재귀 이용 전위, 중위, 후위 순회 구현
이진 트리의 종류
1. 포화 이진트리
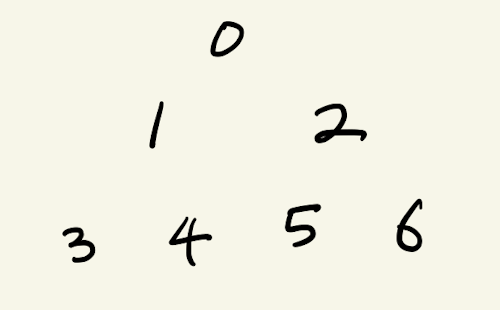
이진트리의 모든 레벨이 꽉 차있는 이진트리.
2. 완전 이진트리
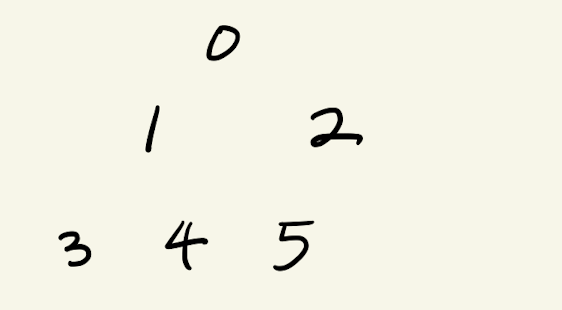
각 레벨에서 앞에서부터 차곡차곡 쌓인 이진트리
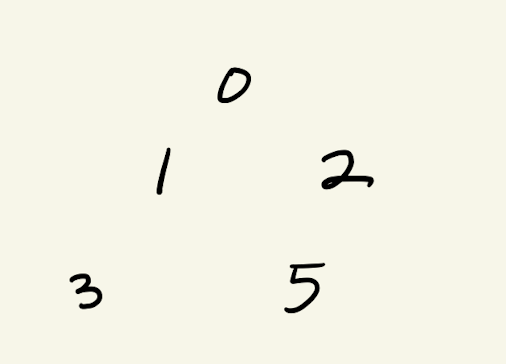
완전 이진트리가 아닌 예. 세 번째 레벨에 하나가 빠져있다.
3. 정 이진트리
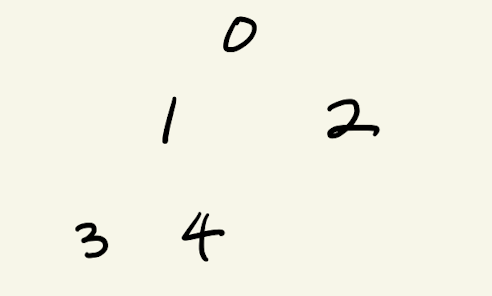
자식이 반드시 0개 또는 2개인 이진트리. 자식이 1개인 노드가 없는 이진트리를 말한다.
이진 탐색 트리란?
-
이진 탐색 시간복잡도 : O(logN). 연결리스트 삽입/삭제 시간잡도 : O(1). 이 둘을 모두 활용할 수 있는 자료구조
-
왼쪽 자식은 자신보다 작고, 오른쪽 자식은 자신보다 큰 이진트리
-
중복값이 없음. (검색 목적 자료구조인데 검색이 느려지므로, 노드에 count를 추가해 사용하자)
-
중위순회로 정렬된 순서를 읽을 수 있음.
-
Java 에서는 TreeSet 과 TreeMap 라이브러리를 통해 구현되어있다.
-
이때 편향 트리를 방지하기 위한 밸런싱을 위해 이진 탐색트리의 개선트리인 레드-블랙트리로 구현됨.
TreeSet
import java.util.TreeSet;
public class TreeSetExam {
public static void main(String[] args) {
TreeSet<Integer> treeSet = new TreeSet<>();
for(int i = 0; i < 10; i++) {
treeSet.add(i);
}
treeSet.remove(9);
Integer score = 5;
System.out.println(treeSet.first());
System.out.println(treeSet.last());
System.out.println(treeSet.ceiling(score));
System.out.println(treeSet.higher(score));
}
} ![]
![]
-
Set 인터페이스의 구현체로 Set과 동일한 메서드들을 갖는다.
-
Set이므로 중복은 불가능하다.
-
삽입삭제는 O(1). 탐색은 O(logN)에 이루어진다.
-
삽입 : add
-
삭제 : remove
-
최대값 반환 : first
-
최소값 반환 : last
-
타겟 이상이면서 가장 가까운 값 반환 : ceiling(t)
-
타겟 이하면서 가장 가까운 값 반환 : floor(t)
TreeMap
import java.util.Map;
import java.util.TreeMap;
public class TreeMapExam {
public static void main(String[] args) {
TreeMap<Integer, String> treeMap = new TreeMap<>();
treeMap.put(1, "샤프");
treeMap.put(2, "지우개");
treeMap.put(3, "볼펜");
treeMap.put(4, "수정테이프");
treeMap.put(5, "색연필");
treeMap.put(6, "사인펜");
treeMap.remove(1);
System.out.println(treeMap);
Map.Entry<Integer, String> entry = null;
entry = treeMap.firstEntry();
System.out.println(entry.getKey() + " " + entry.getValue());
entry = treeMap.lastEntry();
System.out.println(entry.getKey() + " " + entry.getValue());
entry = treeMap.ceilingEntry(4);
System.out.println(entry.getKey() + " " + entry.getValue());
}
}

-
Set과 달리 Map을 상속함으로서 <Key,Value>로 값이 저장된다.
-
Key값 기준 이진탐색트리 형태를 갖는다.
-
삽입 : put()
-
삭제 : remove()
-
최소값 Map.Entry 객체 반환 : firstEntry()
-
최대값 Map.Entry 객체 반환 : lastEntry()
-
타겟 이상이면서 가장 가까운 Map.Entry 반환 : ceilingEntry(t)
