[자료구조]힙

힙이란?

• 우선순위 큐를 위해 만들어진 자료구조

• 우선순위 큐는 우선순위에 따라 데이터 출력순서가 정해지는 큐이다.

• 시뮬레이션이나 작업 스케쥴링에 사용

• 삽입 : O(logN)

• 삭제 : O(logN)

• 완전 이진 트리(각 레벨에서 앞에서부터 쌓이는 이진트리)의 일종이다.

• 힙 트리는 중복값을 허용함.

• 최대힙은 부모값 >= 자식값. 최소힙은 부모값 <= 자식값이다.

---

배열 이용 Max Heap 구현

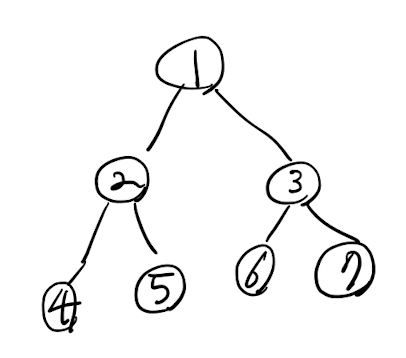
부모 인덱스 : i
왼쪽 자식 인덱스 : i 2
오른쪽 자식 인덱스 : i 2 + 1
구현의 편의를 위해 배열은 1번 인덱스부터 시작

public class MyHeap {
    private int size;
    private int maxHeap[];

    MyHeap(int size) {
        this.size = 0;
        this.maxHeap = new int[size + 1];
    }

    void insert_max_heap(int val) {
        maxHeap[++size] = val;
        // i/2:부모인덱스. i:자식인덱스
        // i/2가 루트가 될때 까지.
        for(int i = size; i > 1; i /= 2) { // 자식이 더 크면 swap
            if(maxHeap[i/2] < maxHeap[i]) {
                swap(i/2, i);
            } else {
                break;
            }
        }
    }

    int del_max_heap() {
        if(size == 0) return -1;

        int root_val = maxHeap[1];
        maxHeap[1] = maxHeap[size];
        maxHeap[size--] = 0;

        for(int i = 1; i * 2 < size; i *= 2) {
            if(maxHeap[i] >= maxHeap[i*2] && maxHeap[i] >= maxHeap[i*2+1]) {
                    break;
            }
            else if(maxHeap[i*2] >= maxHeap[i*2+1]) {
                swap(i, i*2);
                i = i * 2;
            }
            else {
                swap(i, i*2+1);
                i = i * 2 + 1;
            }
        }
        return root_val;
    }

    void swap(int parent_idx, int child_idx){
        int temp = maxHeap[parent_idx];
        maxHeap[parent_idx] = maxHeap[child_idx];
        maxHeap[child_idx] = temp;
    }

    void print_max_heap() {
        for(int i = 1; i <= size; i++){
            System.out.print(maxHeap[i]+" ");
        }
        System.out.println();
    }

    public static void main(String[] args) {
        MyHeap myHeap = new MyHeap(10);

        for(int i = 4; i < 11; i++) {
            myHeap.insert_max_heap(i);
            myHeap.print_max_heap();
        }

        System.out.println();

        for(int i = 0; i < 5; i++){
            int val = myHeap.del_max_heap();
            System.out.println("maxVal = " + val);
            myHeap.print_max_heap();
        }
    }

}

삽입

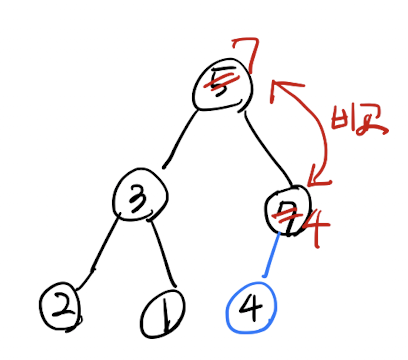
1. 트리의 가장 바깥부분에 삽입 수행 (7)
   

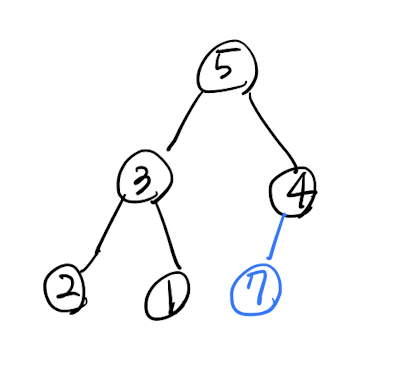
2. 부모와 비교해서 더 크다면 Swap
   

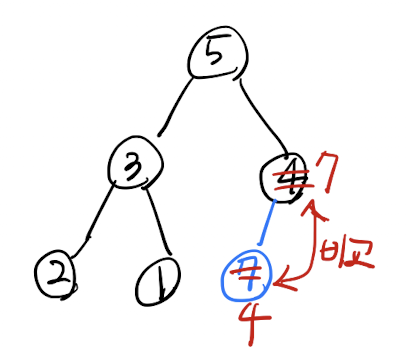
3. 루트노드로 갈 때 까지 반복
   

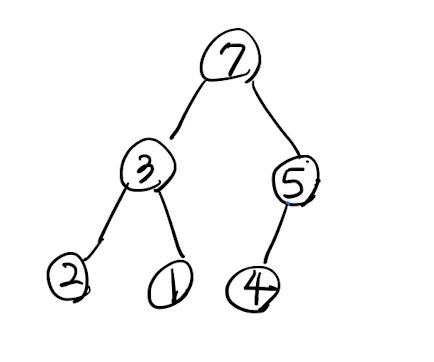
4. 최종 heapify 된 모습
   

삭제

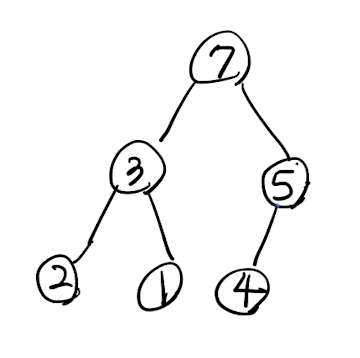
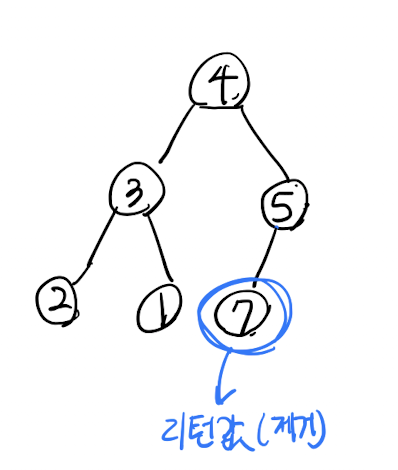
1. 루트에서 삭제가 일어난다.
   

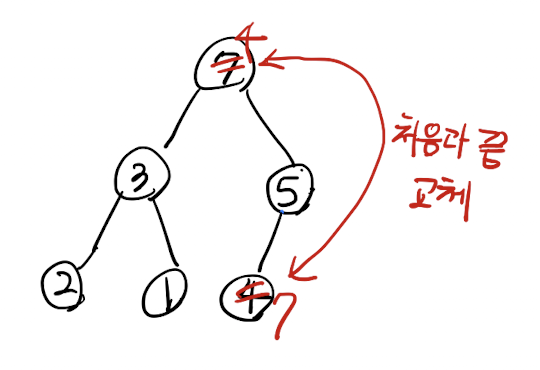
2. 루트와 마지막 노드를 교체함
   

3. 원래 루트값 리턴값으로 사용후 제거
   

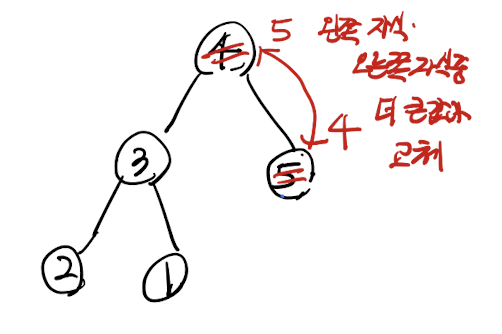
4. 교체된 놈 내려가면서 왼쪽 오른쪽 자식 중 더 큰값과 교체
   

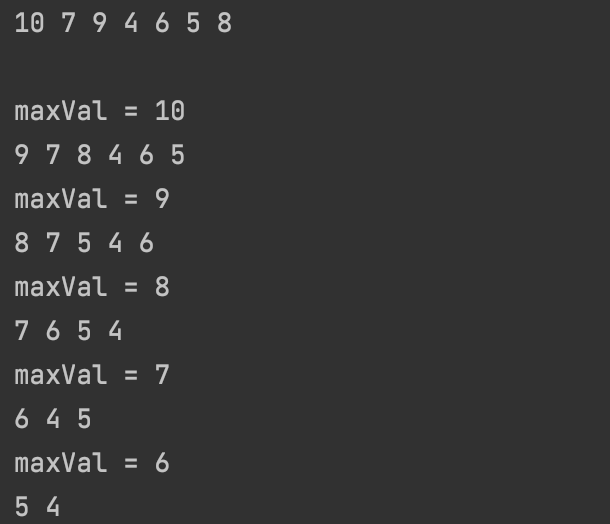
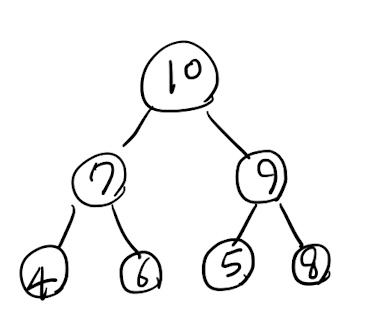
push 결과 heapify를 만족하는 이진트리를 생성하며, Maxheap에 따라 heapify를 유지하며 큰값부터 나오는 것을 확인할 수 있다.

---

PriorityQueue 라이브러리 활용

import java.util.Collections;
import java.util.PriorityQueue;

public class test_priorityQueue {
    public static void main(String[] args) {
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();
        minHeap.add(3);
        minHeap.add(1);
        minHeap.add(5);
        minHeap.add(4);
        System.out.println("=====Minheap=====");
        System.out.println(minHeap.poll());
        System.out.println(minHeap.poll());


        PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder());
        maxHeap.add(3);
        maxHeap.add(1);
        maxHeap.add(5);
        maxHeap.add(4);
        System.out.println("\n=====Maxheap=====");
        System.out.println(maxHeap.poll());
        System.out.println(maxHeap.poll());
    }
}

• PriorityQueue 클래스를 사용한다.

• 기본적으로 Minheap을 생성하며, Maxheap을 생성하려면 인자로 Comparator을 넣어줘야 한다.

• 삽입 : add

• 삭제 : poll