
지난번의 단일 연결 리스트(Single Linked List)를 복습해보자!
- 노드(데이터+포인터)로 구성되어 있으며, 단일 연결 리스트는 데이터+다음 노드의 위치의 형태로 구성되어 있다.
- head와 tail 노드가 있으며, 이 노드들을 통해 삽입과 삭제를 수행한다.
- 삽입/삭제는 O(1), 탐색은 O(n)의 시간 복잡도를 가지고 있다.
- 동적 할당이 기본인 자료구조라 크기를 미리 제한해줄 필요가 없다. (배열은 정적 할당)
단일 연결 리스트는 포인터가 다음 노드의 위치를 가리키고 있어 head -> tail로 이동하는 순이었다.
따라서 탐색 시 최악의 경우, O(n)의 시간 복잡도가 나오곤 했다.
오늘 정리할 이중 연결 리스트(Double Linked List)는 이러한 단방향 탐색을 개선한 양방향 탐색으로
정방향+역방향 탐색도 가능하게 해 좀 더 시간 복잡도를 줄이고자 개선한 것이다.
📗 이중 연결 리스트 (Double Linked List)
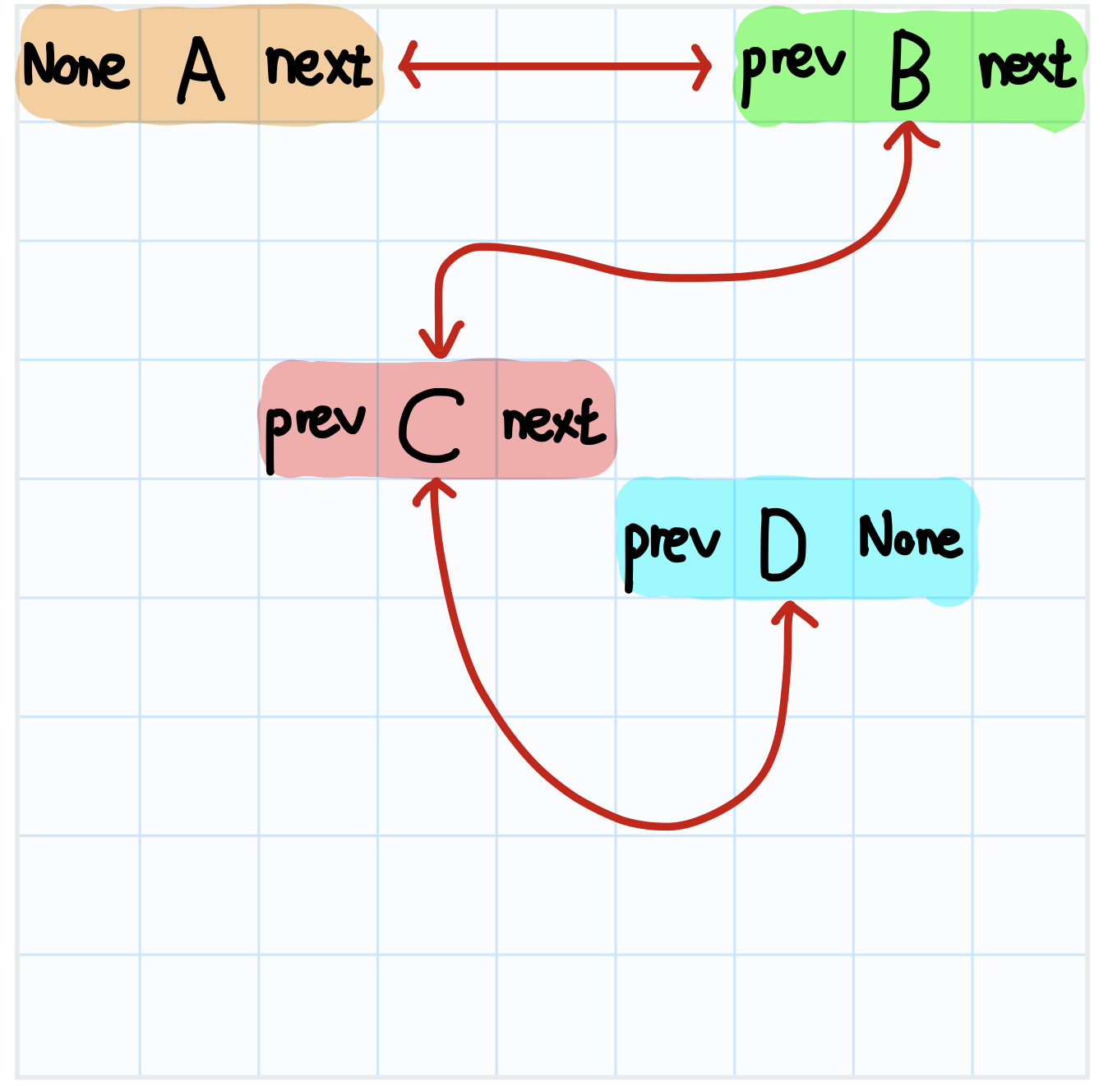
이중 연결 리스트는 그림처럼 단일 연결 리스트 + 포인터(이전 위치)로 구성되어 있다.
💻 Node
class Node:
def __init__(self, data, next = None, prev = None) -> None:
self.prev = prev
self.data = data
self.next = next노드를 생성하는 클래스에서 data, next, 추가로 prev 변수를 생성하도록 프로그래밍하였다.
정방향 + 역방향 조회가 가능한 연결 리스트라서 이전 노드의 위치를 담기 위한 prev 변수를 생성한 것이다.
💻 Main
class main:
def __init__(self) -> None:
self.head = None
self.tail = None연결 리스트의 시작과 끝에 해당하는 head와 tail 변수를 추가해 주었다.
💻 insert
def insert(self,data):
new_node = Node(data)
if self.head is None:
self.head = new_node
self.tail = new_node
else:
new_node.prev = self.tail
self.tail.next = new_node
self.tail = new_node연결 리스트의 맨 끝에 노드를 추가하는 방식으로
tail 변수에 새로운 노드의 정보를 할당하며 tail의 위치를 계속하여 끝으로 지정해주었다.
💻 select_insert
def select_insert(self, data, search_data):
new_node = Node(data)
check_node = self.head # 탐색을 위한 변수
while self.head.data is not None:
if search_data == self.tail.data: # tail 노드의 값이 찾으려는 값과 동일할 때 실행
new_node.prev = self.tail.prev # 새로운 노드의 이전 포인터를 tail 노드의 이전 위치 포인터와 동일하게 설정
self.tail.prev = None # 기존의 tail 노드의 포인터는 삭제
self.tail = new_node # 새로운 노드를 tail 노드로 지정
break
if check_node.data == search_data: # 현재 노드의 값이 찾으려는 값과 동일할 때 실행
new_node.prev = check_node # 새로운 노드의 포인터를 현재 노드의 뒤에 위치하도록 설정
new_node.next = check_node.next
check_node.next = new_node # 현재 노드의 포인터(next,prev)를 재설정
check_node.next.prev = new_node
break
else:
check_node = check_node.next # 찾으려는 값이 일치하지 않을 경우, 다음 노드로 이동먼저 탐색을 위한 변수인 check_node를 하나 생성해 노드를 전부 탐색할 수 있도록 한다.
찾으려는 데이터가 tail 변수의 데이터와 일치하다면 tail 변수를 변경해주고 기존의 포인터 연결은 끊도록 했다.
만약 tail 변수의 데이터와 일치하지 않는다면 check_node 변수를 통해 데이터를 계속 비교해가며 일치하다면 new_node를 노드의 뒤에 위치되도록 포인터를 설정해준다.
💻 select_remove
def select_remove(self, search_data):
check_node = self.head # 탐색을 위한 변수
while check_node.next is not None:
if self.head.data == search_data: # head 노드와 삭제하려는 값이 같을 시 실행
self.head = self.head.next
self.head.prev = None
break
if check_node.data == search_data:
if check_node.next is None: # tail 노드와 삭제하려는 값이 같을 시 실행
check_node.prev.next = None
self.tail = check_node.prev
break
else: # 일반적인 경우, 실행
check_node.prev.next = check_node.next
check_node.next.prev = check_node.prev
check_node.prev = None
check_node.next = None
break
else:
check_node = check_node.nextselect_insert 메서드와 비슷하게 설정하였고, remove 메서드에서는 삭제하려는 값이 head or tail 노드의 데이터와 같을 경우를 모두 추가해주었다.
💻 print_node
def print_node():
iterator = double.head
while iterator:
print(f'iterator prev : {iterator.prev} iterator data : {iterator.data} iterator next : {iterator.next}')
iterator = iterator.next노드의 정보를 모드 출력하는 print_node 메서드에서는 iterator라는 이름의 반복자를 하나 만들어 노드의 정보를 담았다.
🧐 How was it...and?
1. 역방향과 정방향
하필 작성을 마치고 보니 추가하고 싶은 부분들이 생기기 시작한다.
역방향과 정방향이 있다면 노드에 접근할 때 삽입과 삭제 시 정방향으로 가는 방법이 있고, 역방향으로 가는 방법이 있을 것이다. tail과 가까운 노드에 접근할 땐 역방향 조회가 빠를 것이고 head와 가까운 노드에 접근할 땐 정방향 조회가 빠를 것이란 생각이 들었기 때문이다.
다만, 이러한 형태로 작성하지 않은 이유는 삽입과 삭제 모두 결국 어느 방향에서든 시작해서 탐색을 하고 변수에 노드의 인덱스를 담아줘야 하기 때문에 현재 코드와 크게 다르지 않아서이다.
하지만 또 조회와 탐색에 대한 메서드를 추가해야한다면 현재 프로그래밍 방식이 아닌 위에 서술한 방법대로 짜는 게 더 좋을 것이란 생각이 들었다.
이 부분은 추가해서 새로 만들어봐야겠다.
🕒 What is next?
다음 학습 및 정리는 환형 연결 리스트이다.
드디어 연결 리스트의 마지막이다ㅎㅎㅎ 연결 리스트 하나를 배웠다면 나머진 어렵지 않으니 빠르게 가보자👍
