하아...12월 25일이다...😢
솔크에 공부를 하고 있으니 새삼 현타가 온다.
다 때려치고 오늘 하루종일 발로란트나 하려 했지만 오늘 완성한 코드. 지금이라도 정리하자...

---

공부하는 데 가장 오래 걸리고 이해가 어려웠던 트리이다.

정말 100% 트리에 대해 다 알고 있다고 말하긴 어렵지만 지금까지 책을 통해 보고 검색해가며 배운 걸 정리해보자.

---

📗 트리의 특징

앞서 학습했던 배열, 연결리스트, 스택(추가예정...), 데크(추가예정...), 큐(추가예정...)는 모두 선형 자료구조였다.

선형 자료구조는 값이 연속적(1->2->3->4)으로 저장되어 있다는 특성이 있지만
비선형 자료구조는 이와 다르게 자료의 저장이 연속적이라기보단...1:n / n:1의 형태를 띄고 있다.

그 중 오늘 정리할 트리는 이름에 걸맞게 Tree(나무)를 거꾸로 뒤집어 놓은 듯한 모양을 갖춘 계층적인 자료구조이다.

특히 이 자료구조의 모습은 일상생활에서 쉽게 접할 수 있는데 회사나 학교 교무실의 조직도, 집안의 가계도(족보) 등을 보면 이 자료구조와 굉장히 비슷하게 생겼다는 것을 바로 알 수 있다.

여기서 앞서 예시를 든 선형 자료구조들 중 연결 리스트는 다른 자료구조들과 다르게 값들이 띄엄띄엄 선언되어 있어 이 값들을 포인터로 연결해 사용하는 방식이다. 그렇지만 선형 자료구조가 아닌건 아니다. 선형 자료구조는 값들이 연속적으로 저장되는 방식이라는 것에 의의가 있을 뿐, 꼭 그 값들이 무조건 붙어 있어야하는 건 아니다.

---

📗 트리 용어와 특징

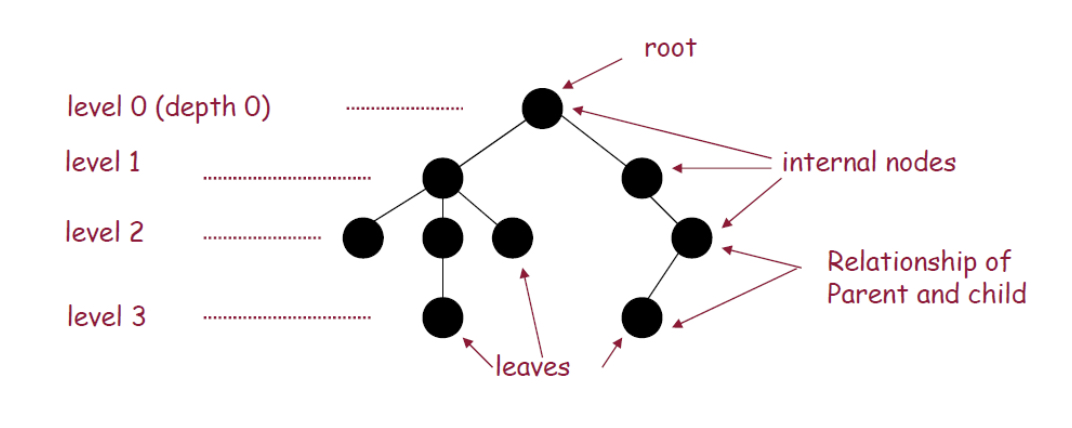
루트(root) : 가장 상위 레벨의 노드로 트리의 시작점이자 하위 노드만 가지고 있는 노드이다.
간선(edge) : 간선, 엣지라고도 불리며 노드와 노드 사이를 이어주는 선이다.
부모-자식(parent and child) : 상, 하위 노드를 기점으로 상위 노드를 부모 노드. 하위 노드를 자식노드라고 말한다.
레벨(level) : 트리의 특정 높이이다. 이진 트리의 경우, 최대 level ^ 2의 노드 개수를 가질 수 있다.
깊이(depth) : 최하위 레벨을 깊이라고 불리며, 리프가 가장 아래에 있을 때를 기준으로 한다.
리프(leaves) : 말단 노드라고도 불리며 자식 노드가 없는 단일 노드를 말한다.

이 외의 두 가지 특징이 있다.

첫번째로는 전체 노드의 개수가 n개일 때, 간선의 개수는 n-1개이다.
두번째로는 해당 노드까지 이동하는 경로는 유일하다 이다. 이 말은 특정 노드까지 이동하는 경로는 간선을 통한 단일 방향뿐이며, 말단이 루트와 연결되는 등의 순환되는 구조를 갖지 않는다는 말과 같다.

📗 이진 트리

트리 자료구조는 종류가 다양하지만 대개 이진 트리를 사용한다.

이진 트리는 하나의 부모 노드 아래로 최대 2개의 자식 노드를 가질 수 있는 트리를 말하며, 이진 트리를 통해서 빠른 탐색을 목표로 하여 사용하고 있다.

이진 탐색 트리가 빠른 탐색을 할 수 있는 이유는 부모 노드로부터 왼쪽에 위치한 노드는 작은 값. 부모 노드로부터 오른쪽에 위치한 노드는 큰 값을 위치시키기 때문에 특정 값을 탐색하고자할 때, 해당 값을 거듭 크기 비교하며 트리를 타고 내려가면 되기 때문이다.

선형 탐색을 기준으로한 배열과의 시간복잡도를 비교해보면 선형 탐색은 우선 앞의 값을 시작으로 순차적으로 값을 꺼내보고 찾고자하는 값을 대조한다. 이때 최악의 경우, 배열의 마지막까지 이동하여 배열의 길이만큼을 반복하게 되고 이에 따라 선형 탐색은 탐색 시 전체 n개의 데이터 중 최대 O(n)의 시간복잡도가 나온다.

반대로 트리 구조로 이루어진 이진 탐색은 루트 아래에 최대 두 개의 자식 노드를 배치할 수 있다.
이때 왼쪽에 위치한 노드는 루트보다 작은 값, 오른쪽에 위치한 노드는 루트보다 큰 값이기 때문에 다음 이동해야할 노드의 위치를 바로 알 수가 있다. 또 이동 후에도 이전과 동일하게 2개의 값 중 대소비교를 통해 다음 이동 위치를 쉽게 파악할 수 있기 때문에 이진 탐색은 탐색 시 전체 n개의 데이터 중 최대 O(log n)의 시간복잡도가 나온다.

또한 이진 트리가 유용하게 사용되는 이유 중 하나는 재귀적인 성질 때문이다.

거대한 하나의 트리는 여러 개의 서브 트리로 나눌 수가 있는데 서브 트리들을 합치면 메인 트리가 만들어지고, 다시 나누면 서브 트리 더미로 분리할 수 있기 때문에 메인 트리에서도 재귀 조건을 통해서 원하는 값을 빠르게 탐색하고 찾아낼 수 있다.

• 여기서 서브 트리란 전체의 트리에서 루트의 왼쪽, 오른쪽 자식을 다시금 루트 노드로 하여 새 트리를 재구성한다고 보면 2개의 트리가 생성되는데 이 트리를 각각 서브 트리라 말하고 루트의 왼쪽 서브 트리 + 오른쪽 서브트리 + 루트 자신을 포함하면 전체 트리가 이루어진다고 볼 수 있다.

📌 이진 트리의 구현 자료형

트리를 작성하는 방식은 크게 두 가지로 배열과 연결리스트가 있다.

두 방식 중 어느 것을 택해도 상관없으나 배열의 경우, 완전 이진 트리가 아니면 쓰이지 않는 빈 공간이 낭비된다. 또 인덱스를 통한 노드 검색을 바탕으로 하기 때문에 다소 트리 작성에 있어서 복잡하다.

• 왜 빈 공간이 낭비되는가?
  완전 이진 트리가 아니면 트리 높이에 따라서 쓰이지 않는 빈 공간이 생길 것이라 판단했다.
  루트의 level이 0일 때, 노드의 개수는 1개이지만 level이 상승하여 5일 때는 level ^ 5.
  
  결국 32개의 리프가 생길 수 있는데, 완전 이진 트리는 이 32개의 리프를 포함한 모든 노드를 사용하지만 그 이외의 트리는 모든 노드를 사용하지 않기에 그만큼 메모리가 낭비될 것이라 생각했다.

📌 이진 트리의 종류

이진 트리는 여러 가지의 종류가 있으며 이 중 책에서 언급된 4가지의 트리(정 이진 트리, 완전 이진 트리, 포화 이진 트리, 편향 이진 트리)를 정리하였다.

1. 정 이진 트리(Full)

정 이진 트리는 각 노드가 2개의 자식 노드를 갖거나 리프 노드인 경우이다. (자식 노드가 아예 없거나 최대 개수인 2개를 모두 갖거나)

2. 완전 이진 트리(Complete)

완전 이진 트리는 마지막 레벨 전까지 노드가 꽉 차있고, 마지막 레벨의 왼쪽에서 오른쪽으로 노드가 채워져 있는 트리이다. 또 이 트리의 경우 마지막 레벨이 다 채워지지 않아도 된다.

3. 포화 이진 트리(Perfect)

포화 이진 트리는 레벨의 노드가 꽉 차 있는 트리로 대체로 최대 힙, 최소 힙 알고리즘에서 쓰이며, 이전에 배열로 구현해 본 바 배열의 모든 메모리를 사용하게 된다.

4. 편향 이진 트리(Degenerate)

편향 이진 트리는 왼쪽이나 오른쪽의 서브 트리만을 가지는 트리이다. 오른쪽을 가졌다면 왼쪽의 서브 트리는 아예 없고, 반대로 왼쪽을 가졌다면 오른쪽의 서브 트리는 아예 없다.

📗 이진 트리의 순회 방식

트리 자료구조는 3가지의 순회 방식이 있다.
해당 3가지 순회 방식은 모두 루트를 시작으로 하지만 탐색한 노드의 출력은 각각 다르다는 특징이 있다.

1. 전위 순회

전위 순회 방식은 현재 노드(부모) -> 왼쪽 노드(자식) -> 오른쪽 노드(자식) 순으로 탐색하는 방식이다.

2. 중위 순회

중위 순회 방식은 왼쪽 노드(자식) -> 현재 노드(부모) -> 오른쪽 노드(자식) 순으로 탐색하는 방식이다.

3. 후위 순회

후위 순회 방식은 왼쪽 노드(자식) -> 오른쪽 노드(자식) -> 현재 노드(부모) 순으로 탐색하는 방식이다.

📗 Programming

이번에 작성한 프로그램은 백준 5639번을 통해서 작성하였다.
해당 문제는 전위 순회를 한 트리의 결과를 입력받고 다시 이 트리를 후위 순회하여 출력하는 문제였다.

초기에 작성한 코드는 내가 생각해도 시간이 오래 걸릴 것 같았다. (아니나 다를까 시간 초과가 발생했다)
최대한 스스로 풀어보려했지만 재귀에 대한 경험이 없어 어떻게 사용해야할 지 감이 잘 오지 않았다.

그래서 다른 분께서 공부한 글을 참고하여 코드를 작성하고 분석하는 방식을 통해 공부를 하였다.

💻 Module

import sys
sys.setrecursionlimit(10**6)

기본적으로 파이썬에서는 재귀의 횟수가 최대 1000번으로 재귀를 진행할 수 있는 깊이가 정해져있는데
sys 모듈에서 제공하는 setrecursionlimit 함수를 통해 재귀의 최대 횟수 값을 변경해주었다.

💻 post_order(tree)

❗왕경고❗
지~인짜 설명이 길다ㅋㅋㅋㅋ 나름 적은 코드량이지만 쪼개고 쪼개며 설명했다.
그치만...숨 한번 크게 들이쉬었다가 내쉬고 읽자(물도 좀 가져오고)

def post_order(tree):
    if len(tree) <= 1:
        return tree
    
    for i in range(1, len(tree)):
        if tree[0] < tree[i]:
            return post_order(tree[1:i]) + post_order(tree[i:]) + [tree[0]]
    
    return post_order(tree[1:]) + [tree[0]]

---

먼저 함수의 입력 값으로는 전위 순회 구조를 갖춘 배열을 받아 사용해주었다.

if len(tree) <= 1:            # 배열의 길이가 1이하이면 실행
        return tree           # 해당 배열을 반환

이후 가장 먼저 만나게 되는 if문에서 배열의 길이가 1이하이면 바로 값을 반환하도록 하였다.
이 부분은 추가로 나중에 설명하게 될텐데 지금으로서는 그냥 인지해두고 다음 반복문을 보자.

for i in range(1, len(tree)):
        if tree[0] < tree[i]:
            return post_order(tree[1:i]) + post_order(tree[i:]) + [tree[0]]

다음 만나는 for문에서는 range(1~트리의 길이)만큼 반복하지만
입력받은 배열의 0번째 인덱스 값은 건너뛰고 1번째 인덱스 값부터 반복하게 된다.

• Why? 반복문의 시작 값은 1일까?
  
  시작 값이 1인 것은 0번째 값을 굳이 반복할 필요성이 없다는 것이다.
  
  이러한 이유는 전위 순회 구조를 보면 조금은 쉽게 이해할 수 있는데 매개 변수로 받게된 배열은 전위 순회 구조를 가지고 있고 이 구조는 Node->Left->Right 순으로 순회하여 트리를 탐색하는 방식이다.
  
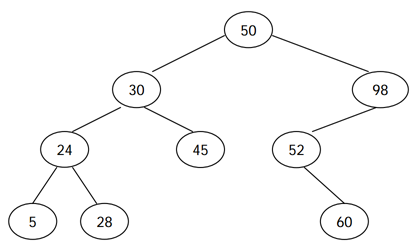
  위의 트리는 문제에서 주어지는 예시 구조인데 이를 전위 순회 구조로 나타내보면 아래와 같다.
  
  Node ---- Left ------ Right
  50 | 30 24 5 28 45 | 98 52 60
  
  하지만 이 구조를 또 쪼개 보면 아래와 같이 나눌 수 있다.
  
  Node - Left - Right
  30 | 24 5 28 | 45
  Node - Left - Right
  98 | 52 | 60
  
  보는 것처럼 각 서브 트리에서 가장 앞에 위치한 값은 Node 즉 루트가 위치하게 된다.
  그리고 이 루트 값을 통해서 우리는 왼쪽 서브트리와 오른쪽 서브트리로 다시 나눌 수 있다.
  
  그럼 다시 처음으로 돌아가보자.
  0번째 값을 굳이 반복할 필요성이 왜 없을까? 그건 0번째 값은 루트 값이기 때문에 이 값을 비교하거나 반복을 할 필요성이 없고, 그 다음 인덱스 값의 대소비교만 진행해도 되기 때문이다.

이 반복문 내에서는 if문이 루트 값과 i번째 값을 입력된 배열의 길이만큼 반복하며 비교한다.
그리고 루트 값보다 큰 값을 찾으면 그 순간 재귀 함수가 실행된다.

if tree[0] < tree[i]:
            return post_order(tree[1:i]) + post_order(tree[i:]) + [tree[0]]

루트 값보다 큰 값을 찾았을 때 재귀 함수가 실행되는 이유는 해당 값이 루트 값의 오른쪽 서브트리에 해당하는 값이기 때문이다. 첫번째 재귀가 if문이 실행되는 조건은 98을 만났을 때임을 알 수 있다.

그리고 이때 반환하는 값은 재귀함수 + 재귀함수 + 루트 노드인데 이걸 자세히 들여다보면
배열 자료형으로 후위 순회 구조인 Left->Right->Node 를 각각 더해주는 것을 알 수 있다.

이렇게 거듭된 재귀로 트리의 리프 노드까지 이동하면 값은 하나가 남거나 혹은 2개의 값만 남게 된다.
이때 값이 하나가 남게된다면 가장 처음 보았던 if문을 통해서 값이 반환된다. 하지만 2개의 값이 남게 된다면 for문 내의 if문 조건을 만족하지 못했다는 것이다.

그말인 즉,
50의 오른쪽 서브 트리인 98 52 60이 이에 해당하며, 이 트리는 우측 노드가 없는 편향 이진 트리에 속한다. 이러한 경우에는 아래와 같이 우측 서브 트리를 제외하고 좌측 서브트리 + 루트 형태로 반환받게 된다.

return post_order(tree[1:]) + [tree[0]]

이는 우측 서브트리는 없으니 L+N형태로 값을 최종 반환할 것이며,
좌측 서브 트리를 통해 재귀하여 다시 값을 탐색하겠다는 의미가 된다.

💻 Main

tree = []
while True:
    try:
        tree.append(int(sys.stdin.readline()))
    except:
        break

nums = post_order(tree)
for i in nums:
    print(i)

메인 실행문은 간단하다. 다만 백준의 문제가 끊임없이 입력을 받고 EOF 발생, 혹은 키보드 인터럽트를 통한 입력의 중단이 전제였기에 try / except 문을 통해 값의 입력을 제어해주었다.

그리고 nums 변수에 배열 형태의 반환 값을 저장하여 이를 하나씩 출력해주었다.