[알고리즘] 최소 신장트리

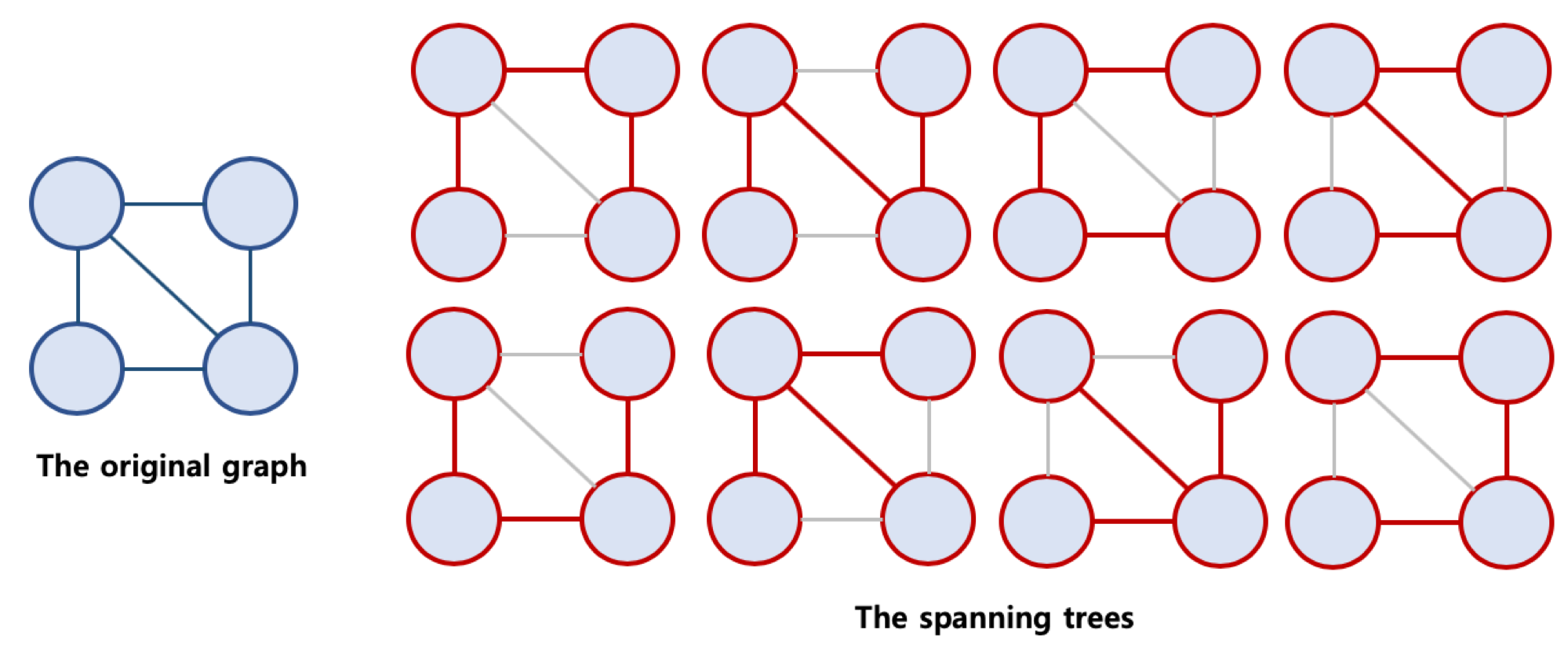
신장트리 (Spanning Tree)

원래 그래프의 모든 노드가 연결되어 있으면서 트리의 속성을 만족하는 그래프

신장 트리의 조건

• 본래 그래프의 모든 노드를 포함해야 함
• 모든 노드가 서로 연결
• 트리의 속성을 만족시킴 (사이클 없음)
  

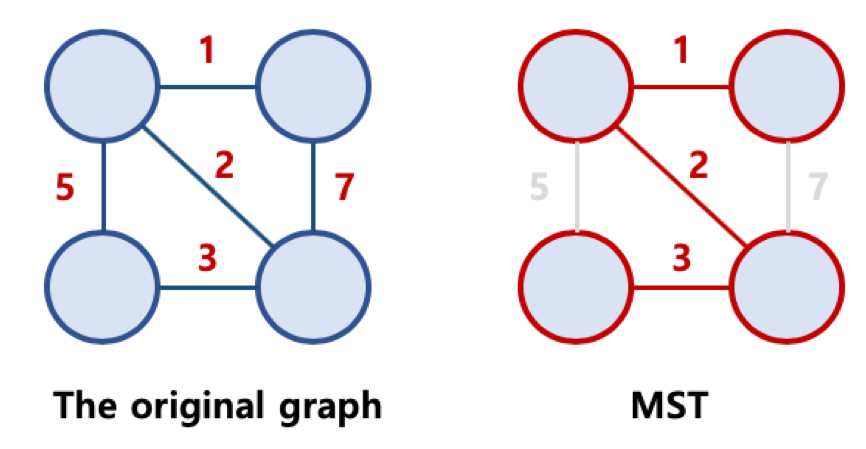
최소 신장트리 (Minimum Spanning Tree, MST)

가능한 신장트리 중에서, 간선의 가중치 합이 최소인 신장트리를 지칭

크루스칼 알고리즘 (Kruskal's algorithm)

간선을 최소비용으로 소팅하고, 최소비용부터 사이클이 안생기는 간선들을 연결한다.
모든 노드들이 다 연결될때까지

프림 알고리즘 (Prim's algorithm)

Union-Find 알고리즘

사이클이 생기는지 체크해서, 생기면 버리고, 안생기면 두 집합 연결.
--> 두 부분집합을 하나의 부분집합으로 합침

union 로직 (집합 구조: 트리 구조)

부분집합의 루트 노드에서 다른 노드를 자식 노드로 연결
두개의 트리를 하나의 트리로 만드는 과정

find 로직

두 노드가 동일한 부분집합에 있는지 체크
각 노드들의 루트 노드가 같은지 확인하면됨

union-by-rank 기법

• 각 트리에 대해 높이(rank)를 기억해 두고, Union시 두 트리의 높이(rank)가 다르면, 높이가 작은 트리를 높이가 큰 트리에 붙임
• 높이가 같은 두 개의 트리를 합칠 때는 한족의 트리 높이를 1 증가시켜주고, 다른 쪽의 트리를 해당 트리에 붙여줌
• 시간복잡도 : O(logN)

path compression

• Find를 실행한 노드에서 거쳐간 노드를 루트에 다이렉트로 연결하는 기법
• Find를 실행한 노드는 이후부터는 루트 노드를 한번에 알 수 있음

크루스칼 알고리즘 코드

그래프

mygraph = {
    'vertices': ['A', 'B', 'C', 'D', 'E', 'F', 'G'],
    'edges': [
        (7, 'A', 'B'),
        (5, 'A', 'D'),
        (7, 'B', 'A'),
        (8, 'B', 'C'),
        (9, 'B', 'D'),
        (7, 'B', 'E'),
        (8, 'C', 'B'),
        (5, 'C', 'E'),
        (5, 'D', 'A'),
        (9, 'D', 'B'),
        (7, 'D', 'E'),
        (6, 'D', 'F'),
        (7, 'E', 'B'),
        (5, 'E', 'C'),
        (7, 'E', 'D'),
        (8, 'E', 'F'),
        (9, 'E', 'G'),
        (6, 'F', 'D'),
        (8, 'F', 'E'),
        (11, 'F', 'G'),
        (9, 'G', 'E'),
        (11, 'G', 'F')
    ]
}

parent = dict()
rank = dict()


def find(node):
    # path compression 기법
    if parent[node] != node:
        parent[node] = find(parent[node])
    return parent[node]


def union(node_v, node_u):
    root1 = find(node_v)
    root2 = find(node_u)
    
    # union-by-rank 기법
    if rank[root1] > rank[root2]:
        parent[root2] = root1
    else:
        parent[root1] = root2
        if rank[root1] == rank[root2]:
            rank[root2] += 1
    
    
def make_set(node):
    parent[node] = node
    rank[node] = 0

def kruskal(graph):
    mst = list()
    
    # 1. 초기화
    for node in graph['vertices']:
        make_set(node)
    
    # 2. 간선 weight 기반 sorting
    edges = graph['edges']
    edges.sort()
    
    # 3. 간선 연결 (사이클 없는)
    for edge in edges:
        weight, node_v, node_u = edge
        if find(node_v) != find(node_u):
            union(node_v, node_u)
            mst.append(edge)
    
    return mst

시간 복잡도

O(E logE)