알고리즘

버블 정렬두 인접한 데이터를 비교해서, 앞에 있는 데이터가 뒤에 있는 데이터보다 크면 자리를 바꾸는 정렬 알고리즘len(arr) - 1 만큼 반복반복문 안에서 len(arr) - index - 1 만큼 반복앞에 있는 데이터가 뒤에 있는 데이터보다 크면 swapswap이

<1>함수 안에서 동일한 함수를 호출하는 형태여러 알고리즘 작성시 사용되므로, 익숙해져야 함재귀 호출은 스택의 전형적인 예파이썬에서 재귀 함수는 깊이가 1000회 이하가 되어야 함시간 복잡도 : O(n)공간 복잡도 : O(n)<2>

동적계획법입력 크기가 작은 부분 문제들을 해결한 후, 해당 부분 문제의 해를 활용해서, 보다 큰 크기의 부분 문제를 해결, 최종적으로 전체 문제를 해결하는 알고리즘상향식 접근법Memoization 기법 사용 (프로그램 실행 시 이전에 계산한 값을 저장하여, 다시 계산하

퀵 정렬 (quick sort)기준점(pivot)을 정해서, 기준점보다 작은 데이터는 왼쪽, 큰 데이터는 오른쪽으로 모으는 함수를 작성각 왼쪽/오른쪽은 재귀용법을 사용해서, 다시 동일 함수를 호출하여 위 작업을 반복함수는 왼쪽 / 기준점(pivot) / 오른쪽 을 리턴

병합정렬재귀용밥을 활용한 정렬 알고리즘 1\. 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.O(n logn)

이진탐색 (Binary Search)탐색할 자료를 둘로 나누어 해당 데이터가 있을만한 곳을 탐색하는 방법분할정복과 이진탐색1\. 분할 정복 (Divide and Conquer) \- Divide: 문제를 하나 또는 둘 이상으로 나눈다. \- Conquer: 나눠진

순차탐색 (Sequential Search): 리스트를 앞에서부터 하나씩 비교하여 원하는 데이터를 찾는 방법O(n)

노드들과 같은 레벨에 있는 노드들(형제노드)을 먼저 탐색하는 방식파이썬에서 제공하는 딕셔너리와 리스트를 활용해서 그래프를 표현할 수 있음BFS 방식: A - B - C - D - G - H - I - E - F - J먼저 탐색할 노드를 start_node로 지정하고,

전체적으로 봤을때는 최적이지 않을 수도 있음

두 노드를 잇는 가장 짧은 경로를 찾는 문제가중치 그래프에서 간선(Edge)의 가중치 합이 최소가 되도록 하는 경로를 찾는 것이 목적단일 출발 및 단일 도착 최단경로 문제 (1:1)단일 출발 최단경로 문제 (1:N) --> 다익스트라 알고리즘전체 쌍 최단경로 (M:N)

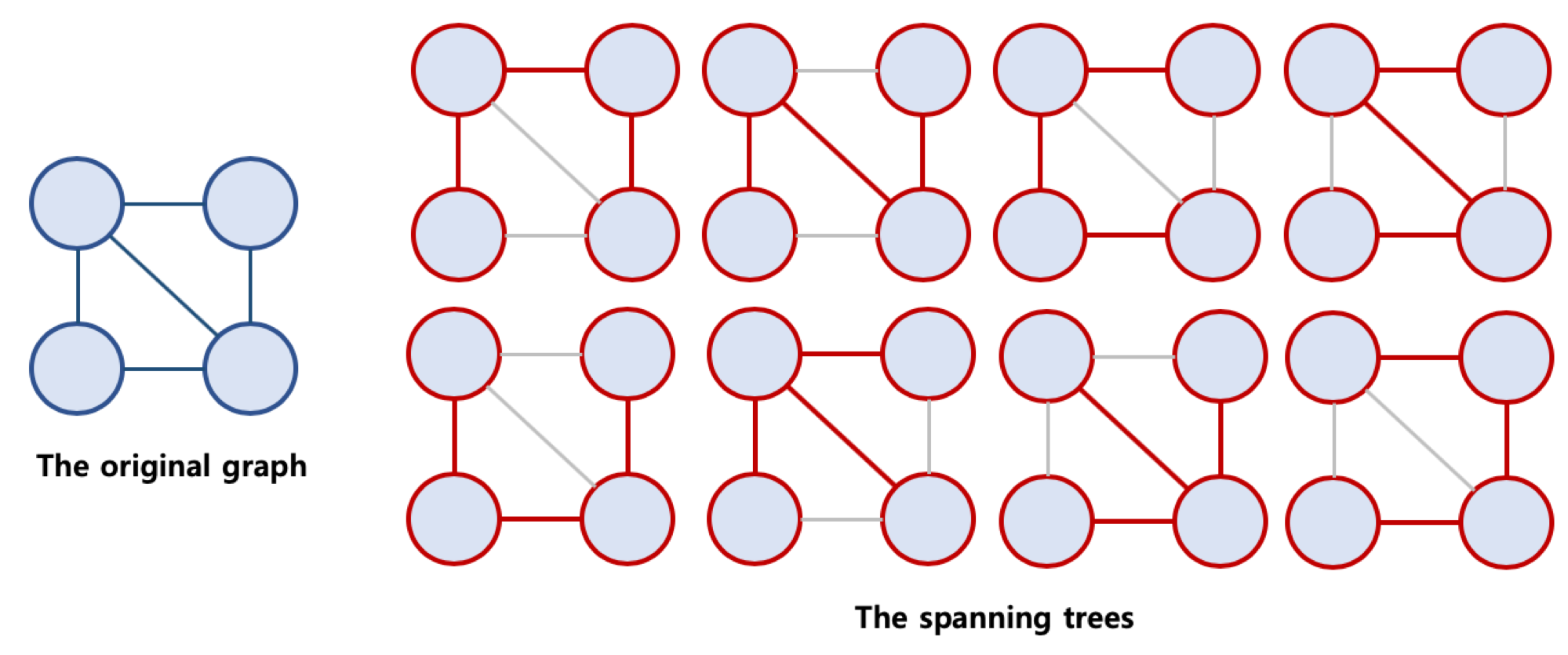
원래 그래프의 모든 노드가 연결되어 있으면서 트리의 속성을 만족하는 그래프신장 트리의 조건본래 그래프의 모든 노드를 포함해야 함모든 노드가 서로 연결트리의 속성을 만족시킴 (사이클 없음)가능한 신장트리 중에서, 간선의 가중치 합이 최소인 신장트리를 지칭크루스칼 알고리즘

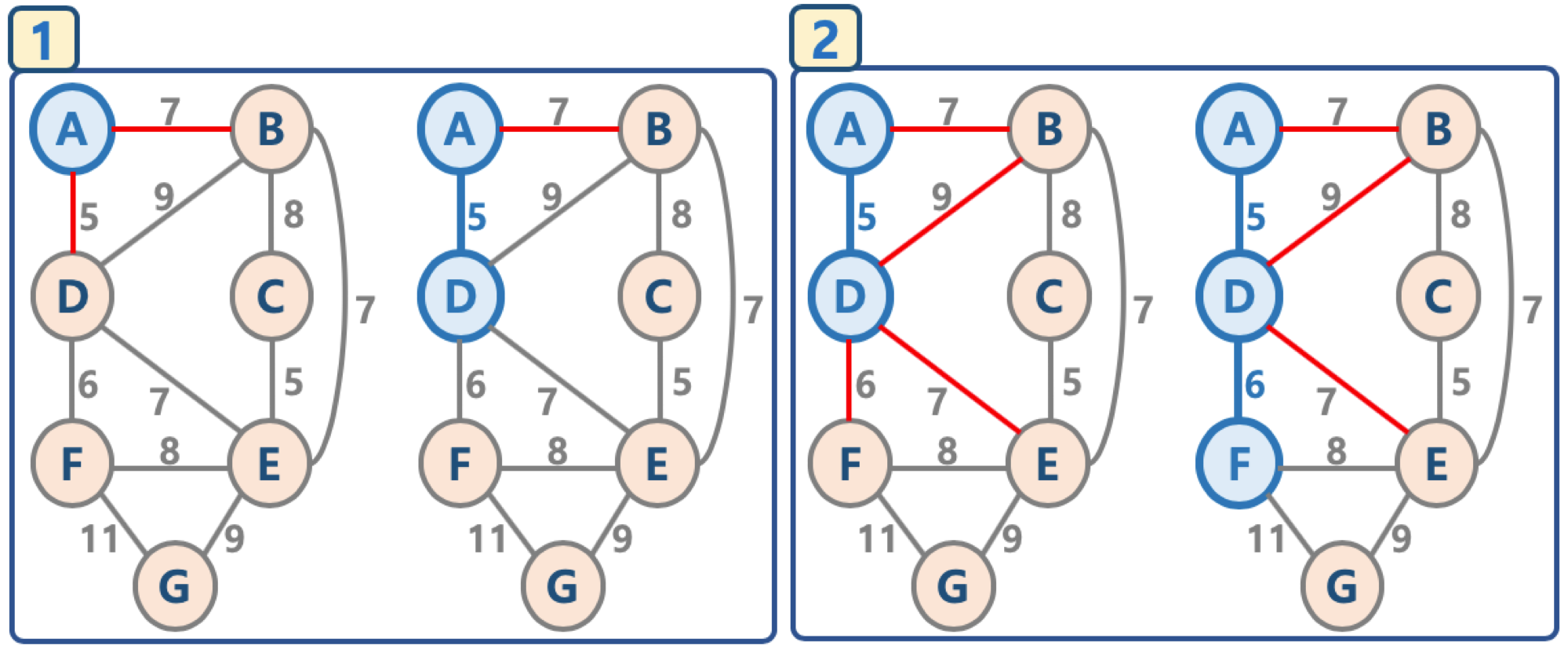
대표적인 신장 트리 알고리즘크루스칼 알고리즘, 프림 알고리즘프림 알고리즘시작 노드를 선택한 후, 정점에 인접한 간선 중 최소 간선으로 연결된 노드를 선택하고, 해당 노드에서 다시 최소 간선으로 연결된 노드를 선택하는 방식으로 최소 신장 트리를 확장해가는 방식크루스칼 알

가장 작은 데이터를 선택해 맨 앞에 있는 데이터와 바꾸고, 그다음 작은 데이터를 선택해 앞에서 두 번째 데이터와 바꾸는 과정을 반복시간 복잡도 : O(N^2)데이터를 하나씩 확인하며, 각 데이터를 적절한 위치에 삽입시간 복잡도 : O(N^2)기준 데이터를 설정하고, 그

리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 차례대로 확인하는 방법코드 : for문 돌리기찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 탐색

다이나믹 프로그래밍 (동적 계획법)큰 문제를 작게 나누고, 같은 문제라면 한 번씩만 풀어 문제를 효율적으로 해결하는 알고리즘 기법재귀함수의 스택 크기가 한정되어 있을 수 있기 때문에, 재귀함수는 가급적 사용하지 말 것.

2차원 매트릭스로 푸는 DFS/BFS

https://developer-davii.tistory.com/90백트래킹 : DFS 원리이긴 한데, 깊이 파고들다가 조건이랑 맞지 않으면 빠꾸하고, 그 가지는 버리고 다른 가지 계속 탐색하는 알고리즘Pruning (가지치기)백준 백트래킹 문제모음