[그래프] 연결 요소

연결 요소. 이름은 거창하지만 사실 뭐 특별한 친구가 아니다.

특별한 친구가 아니긴 한데, 까다로운 친구도 아니긴 한데 처음 보고 뭐지.....? 싶었던 기억이 있어서 족적을 남기기 위해 적는 포스팅이다.

---

연결 요소 (Connected Component)

알고리즘 문제를 풀다 보면 여러 그래프들이 우수수 주어질 것이다. 물론 예쁜 그래프를 통째로 넘겨주는 일은 절대 없고, edge들을 여러개 던져 주며 알아서 잘 하라고 한다.

이때, 보통 이라 쓰고 나만 이라고 이해하는 단어 모든 정점이 예쁘게 다 이어져 있는 그래프가 들어올 것이라고 생각할 수 있는데, 알고리즘 문제는 당신의 생각처럼 인성이 좋은 편은 아니다.

그래프 한개라고 줘 놓고는 여러 component로 뚝뚝 떨어진 그래프들이 있을 수 있는데, 아래의 그림처럼 나누어진 각각의 그래프를 연결 요소라고 한다.

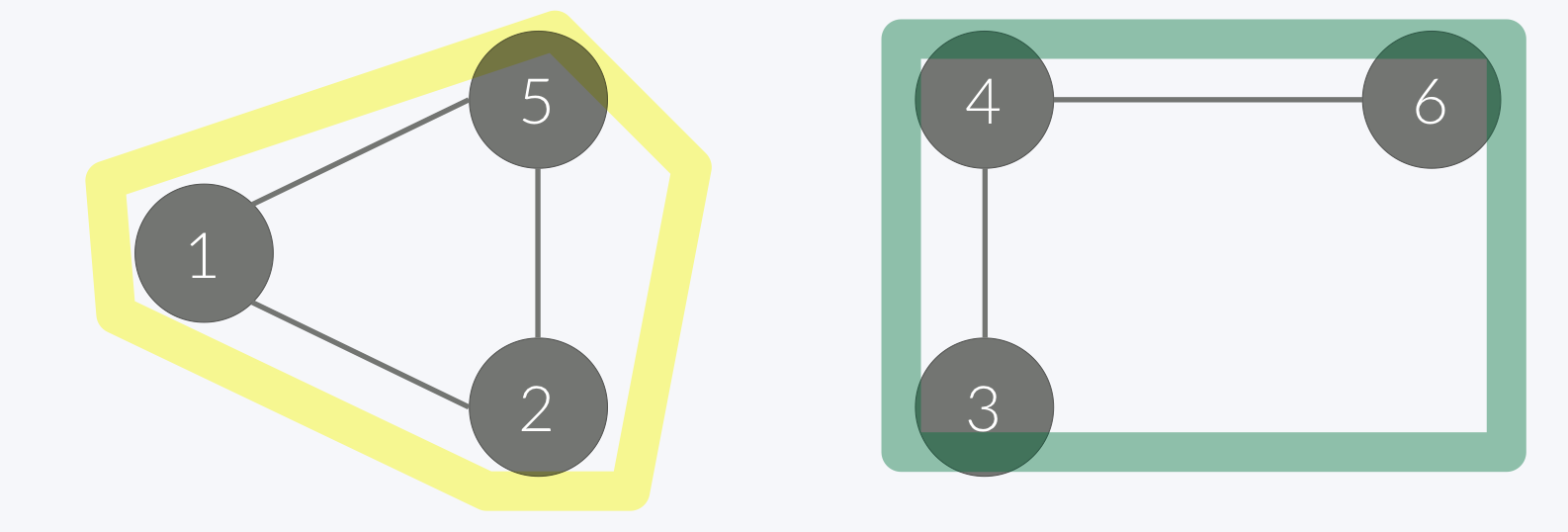
즉, 노란색 덩어리 하나가 연결 요소 하나, 초록색 덩어리 하나가 연결 요소 하나를 차지하여 전체 그래프에는 연결 요소가 2개 존재하는 셈이다.

연결 요소의 탐색 방법

어떤 그래프가 주어졌을 때, 이 전체 그래프에서 연결 요소가 몇 개인지를 뱉어내라고 하면 어떻게 할 것인가?

생각보다 간단하다. 하지만 나는 쉽게 생각해내지 못했지 그냥 각 정점이 아직 방문하지 않았으면 DFS나 BFS를 돌려서 해당 정점이 속해 있는 연결 요소의 모든 정점을 탐색하고, 연결 요소 개수에 +1을 해 주면 된다.

그래프의 탐색 방법인 DFS나 BFS는 간선이 연결되어 있는 정점들 사이만을 탐색할 수 있기 때문에, 끊겨 있는 다른 연결 요소 부분은 DFS나 BFS가 끝난 후에도 탐색이 안 될 것이기 때문이다. 반면, 같은 연결 요소에 속한 정점들은 한번의 DFS나 BFS로 이미 해당 정점을 방문하였다고 check가 될 것이기 때문에, 다시 탐색할 필요는 없다.

연결 요소 관련 문제

백준 11724번: 연결 요소의 개수

아주 기본중에 기본, 연결 요소의 개념만 묻는 문제이지만 보고 당황했다. 뭐 오쪼라눈고야 슈밤

물론 풀긴 했지만.. 미래의 내가 까먹지 말라고 한번 복기해 본다.

우선, 전체 코드는 다음과 같다.

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

void makeGraph(int M, vector<int> *g)
{
    for (int i = 0; i < M; i++)
    {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
}

void bfs(vector<int> *g, bool *check, int v)
{
    queue<int> q;
    check[v] = true;
    q.push(v);

    while (!q.empty())
    {
        int now = q.front();
        q.pop();

        for (int i = 0; i < g[now].size(); i++)
        {
            int next = g[now][i];
            if (!check[next])
            {
                q.push(next);
                check[next] = true;
            }
        }
    }
}

int getConnectedComponent(int N, vector<int> *g)
{
    bool check[N + 1] = {false};
    int ans = 0;

    for (int i = 1; i <= N; i++)
    {
        if (check[i])
            continue;

        bfs(g, check, i);
        ans++;
    }
    return ans;
}

int main()
{
    int N, M;
    cin >> N >> M;
    vector<int> g[N + 1];

    makeGraph(M, g);

    cout << getConnectedComponent(N, g);
}

요새 백준 문제를 풀 때도 기능별로 함수를 떼어 작성하는 습관을 기르고 있는데, 틀린 부분을 찾기도 쉽고 다른 문제에서도 같은 기능을 하는 함수는 기억을 되살려서 비슷하게 작성하면 되니 학습에도 효과가 좋은 듯 하다.

단점이라면.. 아직 함수로 떼는 것이 익숙하지 않아 코드 길이가 쓸데없이 길어져서 마음이 아픈 것?

함수로 떼면서 궁금한 점이 생겼는데, 그냥 main에 모든 기능을 때려박아 작성하는 것 보다 함수로 떼서 작성하는게 수행 시간이 더 오래 걸릴지 궁금하다. 물론 뭔가 함수를 call 하고 그래야하니까 더 오래 걸릴 것 같긴 한데.. 알아봐야겠다

어쨋든 함수별로 어떻게 작성한 것인지 설명해 보도록 하겠다.

main 함수

우선, main 함수는 다음과 같이 단순하게 작성하였다.

int main()
{
    int N, M;
    cin >> N >> M;
    vector<int> g[N + 1];

    makeGraph(M, g);

    cout << getConnectedComponent(N, g);
}

하나의 테스트 케이스에 대해서만 돌리기 때문에 그래프의 정점 개수 N과 간선의 개수 M을 받아 오고, makeGraph를 통해 그래프의 형태를 저장한 뒤 getConnectedComponent에 해당 그래프를 넘겨서 연결 요소의 개수를 리턴하도록 한다.

makeGraph

다음은, makeGraph 함수이다.

void makeGraph(int M, vector<int> *g)
{
    for (int i = 0; i < M; i++)
    {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
}

vector를 이용하여 연결 그래프 형식으로 구현했다. main에서 선언된 vector<int> graph[N+1]을 해당 함수에서 수정할 수 있어야 하므로, call-by-reference 방식으로 변수를 넘겨 받았다.

가중치가 없는 양방향 그래프이므로, 단순 push_back을 통해 그래프의 형태를 저장할 수 있다.

makeGraph 함수를 실행하는데는 for loop이 간선의 개수만큼 반복되기 때문에, $O(E)$의 시간이 걸린다고 할 수 있다.

getConnectedComponent

다음은 가장 핵심이 되는, 주어진 그래프에서 연결 요소의 개수를 구하는 getConnectedComponent 함수이다.

int getConnectedComponent(int N, vector<int> *g)
{
    bool check[N + 1] = {false};
    int ans = 0;

    for (int i = 1; i <= N; i++)
    {
        if (check[i])
            continue;

        bfs(g, check, i);
        ans++;
    }
    return ans;
}

먼저, 그래프에 대한 정보를 받아 와야 하기 때문에 main함수에 정의되어 있는 vector<int> graph[N+1]을 받아 오기 위해 call-by-reference 형식을 이용하였다.

이 함수에서는 graph에 대한 정보를 변경하지 않기 때문에 call-by-value 형식으로 받아와 local-value 타입으로 사용해도 상관은 없지만, call-by-value 형식으로 받아 올 경우 추가적인 메모리 공간이 필요하기 때문에 call-by-reference 형식을 선호한다.

다음으로는 별게 없다. 각 정점에 대해 for loop을 돌리면서, 해당 노드를 아직 방문하지 않았으면 bfs 탐색을 통해 하나의 연결 요소에 포함된 모든 노드를 방문한다. bfs를 한번 할 때마다 연결 요소가 하나씩 추가되는 것이므로, 정답으로 return이 될 ans를 +1 해 준다.

getConnectedComponent 함수를 실행하는데는 bfs(g, check, i); 부분이 수행 시간에 많은 영향을 미치는데, 주어지는 그래프의 연결 요소의 개수에 따라 해당 라인을 반복할 횟수가 달라진다.

bfs는 연결 리스트를 이용하여 구현했는데, 이때 연결 요소가 개입하기 때문에 bfs의 탐색 시간을 잘 생각해 보아야 한다.

bfs는 연결 요소가 몇 개이든지 간에, 전체 그래프에서 각 정점을 한번씩만 방문하고, 각 간선을 한번씩만 방문한다.

음 이걸 어떻게 말로 설명해야 할지 모르겠는데, getConnectedComponent 함수가 bfs를 한번 부를 때, 전체 그래프에 대한 bfs 탐색을 하는 것이 아니라 해당 정점이 속한 연결 요소 부분만 bfs 탐색을 하게 된다. 따라서, getConnectedComponent의 for loop을 탈출을 할 시점에서 따져야 전체 그래프에 대하여 모든 정점, 모든 간선을 한번씩 탐색하게 되는 것이다.

따라서, getConnectedComponent를 수행하는데 걸리는 시간은 전체 그래프를 BFS 탐색할 때 걸리는 시간과 동일하므로, $O(V+E)$라고 할 수 있다.

전체 시간 복잡도 따져보기

main함수는 makeGraph와 getConnectedComponent를 한 번씩 call하게 된다. makeGraph함수는 수행 시간이 $O(E)$ 이고, getConnectedComponent는 수행 시간이 $O(V+E)$ 이다.

따라서, 전체 수행시간은 $O(V + 2E)$, 즉 $O(V+E)$라고 할 수 있다.