[ 트리 ] 트리의 기초

트리.. 그래프에 이어 많이 들어보고 많이 안다고 생각하는 친구이나, 사실상 아무것도 아는 게 없었던 친구.

오늘 이후로 트리 까먹지 말자 제발

---

트리의 정의

트리의 정의는 다음과 같다.

자료구조의 일종이며, 사이클이 없이 모든 정점이 연결되어있는 그래프이다. 사이클이 없는 그래프이므로 정점의 개수가 V개이면 간선의 개수는 V-1개이다.

이 두줄을 만족하는 것이 트리이다. 여기서 한 가지 주목해야 할 점은, 왼쪽 자식이 어쩌구, 오른쪽 자식이 어쩌구 이딴 얘기는 트리의 정의에 포함되지 않는다는 점이다.

또한, 루트가 있어야 한다는 조건 이런것도 없다. 보통 트리에서 하도 루트를 언급하다 보니 루트가 당연히 있어야 한다고 생각할 수 있는데, 루트가 없는 트리도 존재한다.

트리는 그저 사이클이 없이 모든 정점이 연결되어있는 그래프이므로, 하나의 노드에 자식 노드가 여러개일 수 있다.

어떤 것이 트리일까?

트리의 정의가 사이클이 없이 모든 정점이 연결되어 있는 그래프. 정점의 개수가 V개이면 간선의 개수가 V-1개 라고 하였다.

그렇다면, 다음의 1과 2는 모두 트리라고 할 수 있을까?

1. 사이클이 없는 연결 그래프이다.
2. 정점의 개수가 V개이고, 간선의 개수가 V-1개이다.

답을 말하자면, 1은 트리가 맞지만 2는 트리가 아닐 수도 있다.

사이클이 없는 연결 그래프이면 당연히 정점의 개수가 V개이고, 간선의 개수가 V-1개이므로 트리의 조건을 만족한다. 그러므로 1은 트리라고 할 수 있다.

반면, 정점의 개수가 V개이고 간선의 개수가 V-1개라는 것만 가지고는 트리라고 할 수 없다. 다음과 같은 반례가 있기 때문이다.

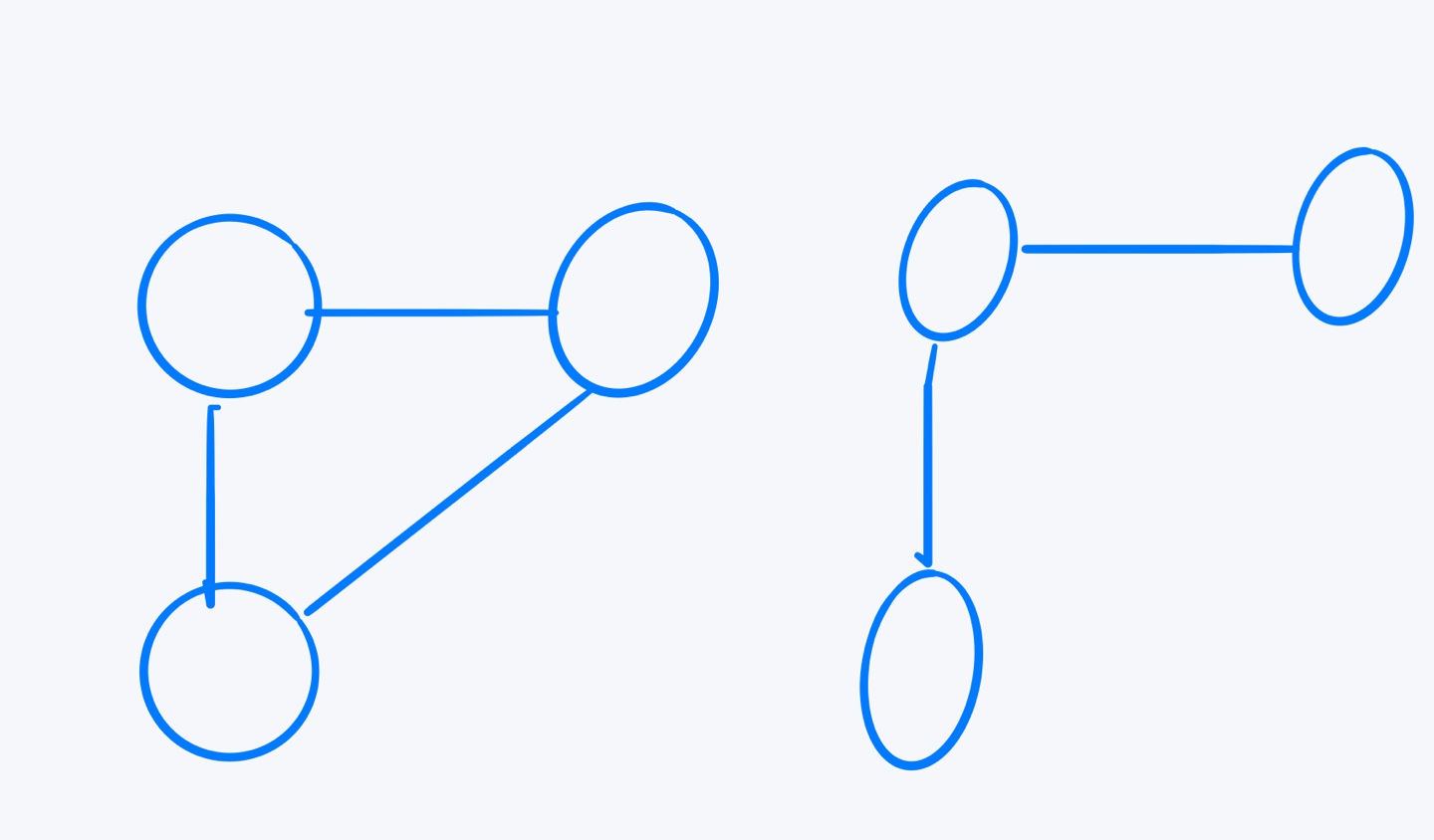
위의 그림은 분명 정점이 6개이고, 간선이 5개이지만 누가 봐도 트리는 아니다.

정점의 개수가 V개이고 간선의 개수가 V-1개라는 단서로 트리임을 말하기 위해서는 여기에 모든 정점이 연결되어 있다 라는 조건이 붙어야 한다.

즉, 정점의 개수가 V개이고 간선의 개수는 V-1개이며, 모든 정점은 연결되어 있다 라고 할 경우에만 트리라고 할 수 있다.

루트 있는 트리 (Rooted Tree)

그냥 뭐 별거 없다. 이름은 거창한데 그저 루트가 정해져 있으면 루트 있는 트리라고 한다. 모든 정점이 루트 노드로 사용될 수 있지만, 보통 1번 정점을 루트로 많이 사용한다.

루트가 정해질 경우 할 수 있는 일들이 생긴다.

Root node & Leaf node

1. 트리의 방향을 정할 수 있다.
   루트를 제일 위로 두고, 루트부터 아래로 뻗어나가게 방향을 정할 수 있다.

2. parent-child 관계를 만들 수 있다
   root node : 부모 노드가 없는 노드
   terminal (left) node : 자식 노드가 없는 노드

Sibling

부모 노드가 같은 노드끼리는 형제 노드이다.

트리의 깊이 (depth)

루트에서부터의 거리를 말한다.

루트의 깊이를 0으로 할 수도 있고, 1로 할 수도 있다. 기준만 잘 잡으면 된다.

이 문제는 어떤 것을 배열에 저장할 때 index 1부터 할 것인지, 0부터 할 것인지 정도의 차이이다. 의미 없다는 뜻

트리의 높이 (height)

트리의 depth중 가장 큰 값을 트리의 높이라고 한다.

조상, 자손

정점 p에서 정점 q로 갈 수 있는 경로가 있을 때,
정점 p가 정점 q보다 루트에 가까운 노드이면
정점 p는 정점 q의 조상이고
정점 q는 정점 p의 자손 노드이다.
이때, 정점 p또한 정점 p의 조상이다. 즉, 자기 자신도 조상에 속한다.

정점정점정점정점 뭔소린지 모르겠으니 예시를 통해 이해해보자.

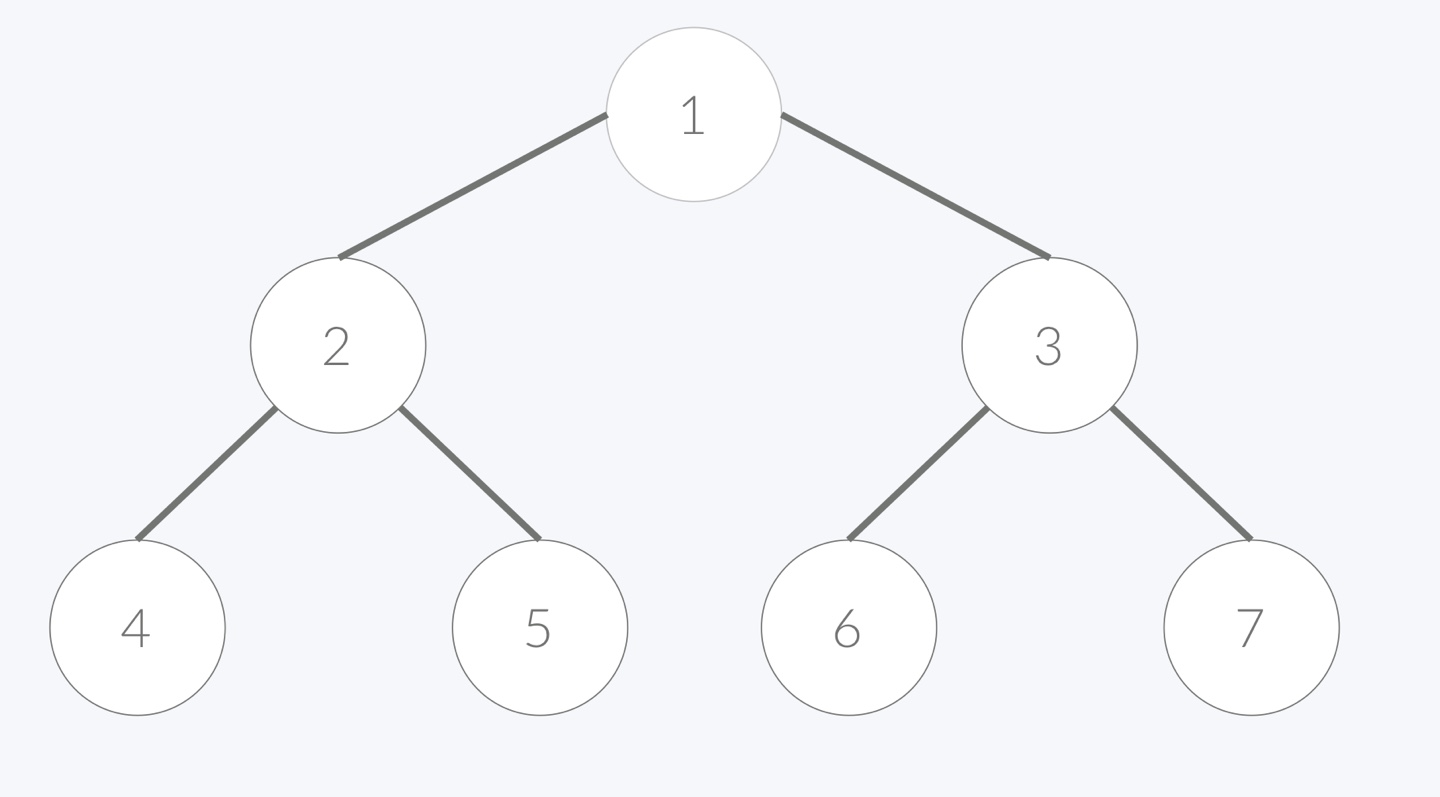
루트 노드가 정점 1일때, 정점 4의 조상은 4, 2, 1번 정점이다.

조상에는 자기 자신도 포함된다는 것을 기억할 것!

이진 트리 (binary tree)

자식을 최대 2개만 가지고 있는 트리이다.

항상 2개가 아니라는 점을 명심할 것!

자식을 항상 2개 가지고 있는 트리는 완전 이진 트리(complete binary tree)이다.