알고리즘 Convex hull - Graham

볼록다각형이란?

내각의 크기가 180도 넘지 않는 단순 다각형을 의미힙나디. 사진을 예로 들면

볼록다각형

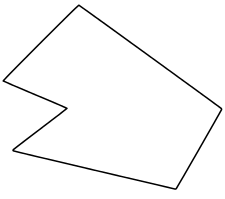
오목다각형

Convex hull 알고리즘

즉 임의의 점들이 주어지면 이 점들을 이용한 볼록다각형을 완성하면 됩니다. 다음과 같은 흐름으로 구현했습니다.

Idea

시작점 선택

우선 시작점을 선택해야 진행할 수 있겠죠? 이번 알고리즘에서는 점들을 반시계 방향으로 탐색할 것이기 때문에 x값이 가작 작은 점을 기준으로 했고 x값이 최소인 점이 여러 개 있다면 그 중에서 y값이 최소인 점을 시작점으로 선택했습니다.

각 정렬

점들을 이어 다각형을 만들기 위해선 순서가 필요합니다. 각 정렬은 평행사변형 포스트에서 다뤘기 때문에 링크를 남기겠습니다.
평행사변형 포스트 링크

Left Turn or Right Turn?

우선 점들을 탐색하는 방향을 결정해야합니다. 전 반시계 방향으로 순회하기로 했습니다. 이 때 반시계 방향으로 진행하면서 내각이 180도 이하인지 판별하기 위해서는 다음 진행 방향이 좌회전인지 우회전인지로 판별할 수 있습니다.

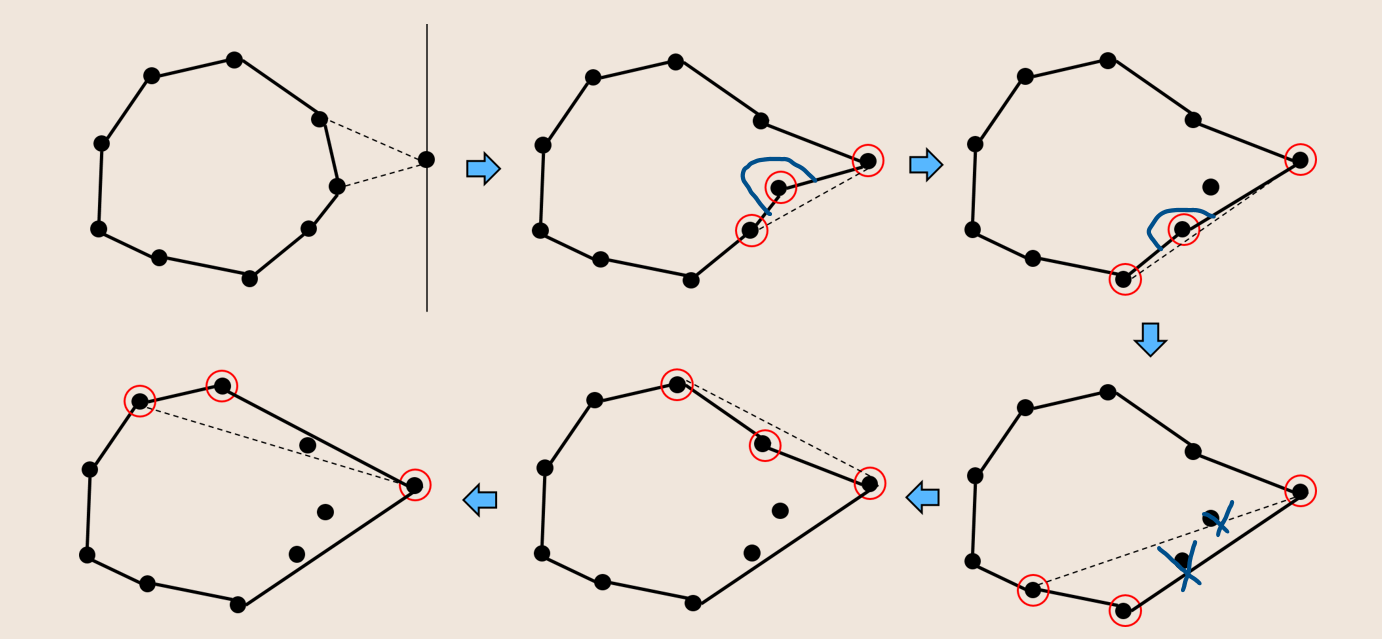
2번에서 다음 정점을 찾아 이어보려고 했더니 우회전(내각이 180도 이상)을 해야만 진행할 수 있다는 것을 식벽하여 롤백하는 모습입니다. 3번도 마찬가지로 다음 정점으로 향하기 위해서 우회전을 해야하기 때문에 역시 롤백합니다. 이 과정을 통해 오직 좌회전만으로 모든 점을 순회했다면 볼록다각형을 완성한 것입니다.
아 때 진행방향 판별을 세 점을 외적한 결과값의 부호를 이용합니다.

진행하는 점 관리는 stack으로

진행 과정에서 선택된 점을 따로 보관하기 위해 stack에 관리합니다. stack에 관리하면 빠르 속도로 점을 추가하거나 지울 수 있습니다.

Left Turn + stack

회전각을 알기 위해서는 세 점이 필요합니다. for 문을 사용한다고 하면 i값이 현재 진행할 점이고 stack의 top은 중간점, 그 다음은 현 상황에서의 출발점입니다.
코드를 예로 들겠습니다.

 for(int i =2 ; i<points.length;i++){
            Point three = points[i];
            Point two = stack.pop();
            Point one = stack.peek();
            while(!stack.empty() && !leftTurn(one,two,three)){
                two = stack.pop();
                if(!stack.empty())
                    one = stack.peek();
            }
 }

코드 설명

    @Override
    public int compareTo(Point o) {
    // 각과 거리를 이용하여 점을 정렬
    
        double angle1 = calAngle(startPoint, this);
        double angle2 = calAngle(startPoint, o);
        if (angle1 < angle2) return -1;
        else if (angle1 > angle2) return 1;
        else return dist(this,o);
    }
    // 세 점을 통해 좌회전 여부 판별
    static private boolean leftTurn(Point a, Point b, Point c){
        return ccw(a,b,c)>0;
    }
    // 세 점을 외적한 결과값이 양수이면 좌회면 음수이면 우회전임
    static private int ccw(Point a, Point b, Point c){
        int result = (a.x * b.y + b.x*c.y+ c.x*a.y) - (b.y * c.x + a.x * c.y + a.y*b.x);
        if(result>0) return 1;
        else if(result<0) return -1;
        else return 0;
    }
    // stack의 push, peek를 적절히 활용하여 관리
    static Stack<Point> graham(Point [] points){
        stack.push(Point.startPoint);
        stack.push(points[1]);
        for(int i =2 ; i<points.length;i++){
            Point three = points[i];
            Point two = stack.pop();
            Point one = stack.peek();
            while(!stack.empty() && !leftTurn(one,two,three)){
                two = stack.pop();
                if(!stack.empty())
                    one = stack.peek();
            }
            stack.push(two);
            stack.push(three);
        }
        return stack;
    }