알고리즘 도형 판별 - 평행사변형

김정훈·2024년 4월 1일

점 4개의 좌표가 주어지면 이 점들이 이루는 도형이 평행사변형인지 판별하는 알고리즘입니다.

판별 전 세팅

점 4개가 임의로 주어지기 때문에 도형의 변이 어떻게 형성되는지 알 수가 없습니다. 때문에 시작점 및 점의 순서를 임의로 선정하여 도형을 판별해야 합니다.

y값이 가장 작은 점

y값이 가장 작은 점을 시작점으로 합니다. 이 때 y값이 동일한 점이 있다면 그 중 x값이 가장 작은 점을 선택합니다.

각 정렬

도형의 변을 시작점을 기준으로 연결하기 위해서는 각 점들과 시작점 사이의 선이 x축과 이루는 각을 이용하여 정렬을 해야합니다.

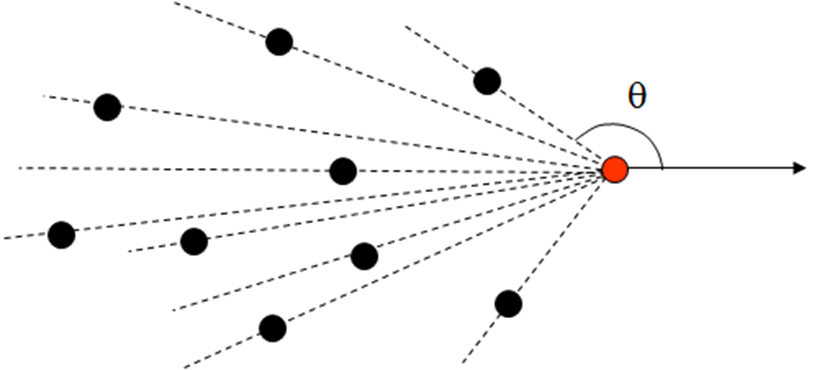
그럼 네 점이기 때문에 점1과 2가 이루는 변1, 점2와 점3이 이루는 변2.... 점4와 점1이 이루는 변4가 완성됩니다.

평행사변형 이론

두 쌍의 대변이 평행

이 점을 이용한다면 마주보는 사잇각의 각도 비교, 대변의 기울기값 비교 등을 시도할 수 있습니다.

대변의 길이가 같음

즉 대변의 길이 비교를 이용할 수 있습니다.

전 대변의 길이와 기울기를 비교했습니다.

코드

각 정렬

    @Override
    public int compareTo(Point o) {
        double angle1 = calAngle(startPoint, this);
        double angle2 = calAngle(startPoint, o);
        if (angle1 < angle2) return -1;
        else if (angle1 > angle2) return 1;
        else return dist(this,o);
    }
    
    static double calAngle(Point a, Point b) {
        return Math.atan2((b.y - a.y), (b.x - a.x));
    }

두 점을 이용해 atan2 연산을 사용합니다. 이 연산을 통해 두 점이 이루는 선과 x축사이의 각을 구할 수 있습니다. 만약 각이 같다면 선의 길이값을 통해 정렬합니다. 길이 공식은 생략하겠습니다. 이것은 java의 comparable을 이용한 것이고 이와 동일한 성능을 직접 구현하려면 merge sort를 구현하는 것이 좋습니다.
merge sort를 이용한 각 정렬을 직접 구현한 포스트의 주소를 남겨놓겠습니다.
merge sort post link

평행사변형 판별

	static boolean isParallel(Point p1, Point p2, Point p3, Point p4) {
		int dx1 = p1.x - p2.x;
		int dy1 = p1.y - p2.y;
		int dx2 = p3.x - p4.x;
		int dy2 = p3.y - p4.y;
		int crossProduct = dx1 * dy2 - dy1 * dx2;
		return crossProduct == 0;
	}