[알고리즘] 기수 정렬 Radix Sort

    데이터를 구성하는 기본 요소 (Radix)를 이용하여 정렬을 진행하는 방식. 하나의 기수마다 하나의 버킷을 생성하여 분류를 한 후, 버킷 안에서 정렬을 한다.

• 비교(comparison) 정렬의 한계는 O(nlogn)
  => 기수 정렬은 non-comparison sort로 이 한계를 넘어설 수 있다.
• 비교하려는 데이터의 길이가 다르다면 비효율적
• 안정 정렬(stable)
• MSD (Most-Significant-Digit): 가장 큰 자리수부터 정렬한다. 중간 정렬 결과를 알 수 있다.
• LSD (Least-Significant-Digit): 가장 낮은 자리수부터 정렬한다. 정렬하고자 하는 데이터의 길이가 다르면 큰 데이터의 자리수만큼 따져야 한다
  => LSD 주로 사용
  => 정렬 시 큰 자리수가 우선시되어야함. MSD는 큰 자리수를 먼저 정렬해버려서 다음 자리수를 정렬 할 때 이미 정렬된 순서가 흐뜨러질 수 있다. 따라서 정렬이 되었는지 확인하는 과정이 필요하고, 이 때문에 메모리를 더 사용한다. 참고링크
• 문자열, 정수 정렬 가능
• 부동소수점처럼 자릿수가 없다면 정렬 불가능
• 전체 요약
  
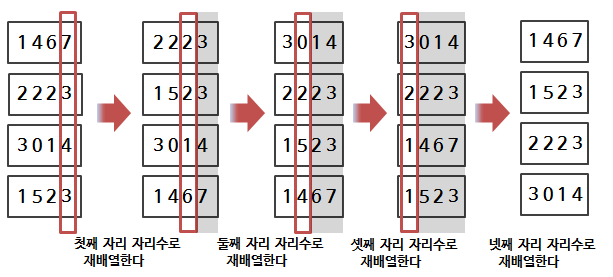
• 상세 과정
  
  
  
  
  

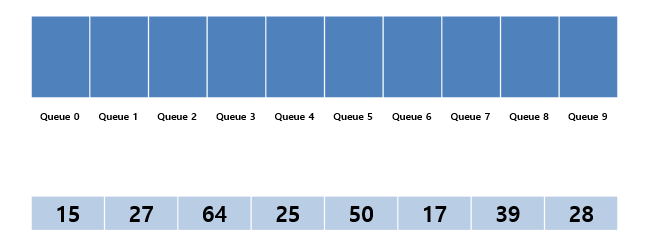
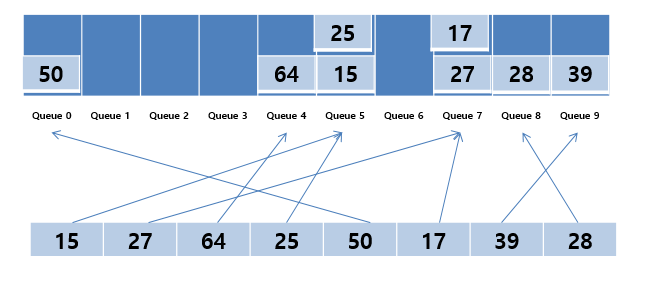
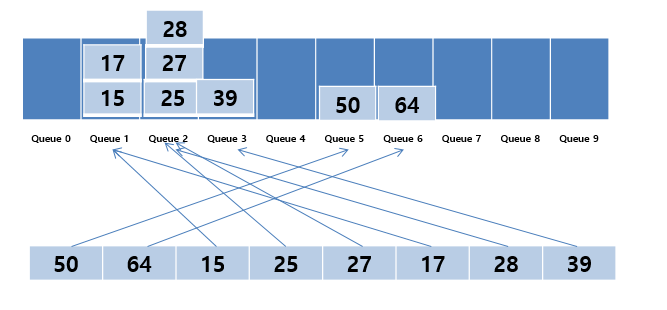
1. queue 자료구조의 0~9 까지의 Bucket을 준비한다.
2. 모든 데이터에 대하여 가장 낮은 자리수에 해당하는 Bucket에 차례대로 데이터를 둔다.
3. 0부터 차례대로 버킷에서 데이터를 다시 가져온다.
4. 가장 높은 자리수를 기준으로 하여 자리수를 높여가며 2번 3번 과정을 반복한다.

• 코드

#include<iostream>
#include<cstdlib>
#include<ctime>
#include<queue>
 
#define MAX 100
using namespace std;
 
int Max_Value;
int Arr[MAX];
bool Flag[10001];
queue<int> Q[10];
 
void Print()
{
    cout << "####################################################################################################################" << endl;
    int Cnt = 0;
    for (int i = 0; i < MAX; i++)
    {
        printf("%6d ", Arr[i]);
        Cnt++;
        if (Cnt == 20)
        {
            Cnt = 0;
            cout << endl;
        }
    }
    cout << "####################################################################################################################" << endl;
    cout << endl;
}
 
void Radix_Sort()
{
    int Radix = 1;
    while (1)
    {
        if (Radix >= Max_Value) break;
        Radix = Radix * 10;
    }
    for (int i = 1; i < Radix; i = i * 10)
    {
        for (int j = 0; j < MAX; j++)
        {
            int K;
            if (Arr[j] < i) K = 0;
            else K = (Arr[j] / i) % 10;
            Q[K].push(Arr[j]);
        }
 
        int Idx = 0;
        for (int j = 0; j < 10; j++)
        {
            while (Q[j].empty() == 0)
            {
                Arr[Idx] = Q[j].front();
                Q[j].pop();
                Idx++;
            }
        }
    }
}
 
int main(void)
{
    srand((unsigned)time(NULL));
    for (int i = 0; i < MAX; )
    {
        Arr[i] = (rand() % 10000) + 1;
        if (Flag[Arr[i]] == false)
        {
            Flag[Arr[i]] = true;
            if (Max_Value < Arr[i]) Max_Value = Arr[i];
 
            i++;
        }
    }
    
    cout << "[ Initialize Array State ] " << endl;
    Print();
    Radix_Sort();
    cout << "[ After Sort Array State ] " << endl;
    Print();
 
    return 0;
}

• 시간 복잡도
  d: 정렬할 숫자의 자릿수, n: 데이터 개수, k: 범위(최대값, 10으로 고정)

  시간복잡도
  최선	Ω(nk)
  평균	Θ(nk)
  최악	O(nk)

  => O(d(n+K))

• 공간 복잡도: O(n+k)

참고링크1
참고링크2