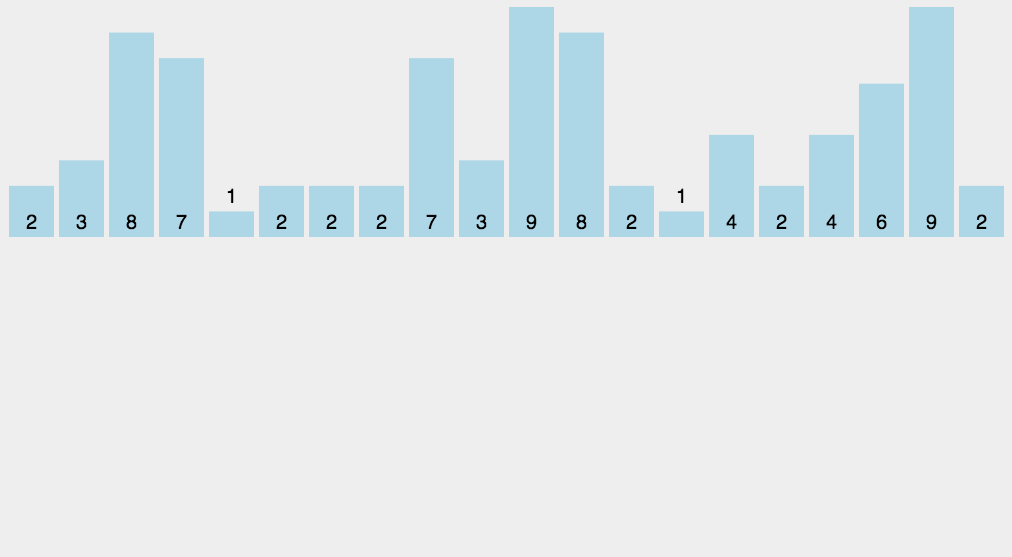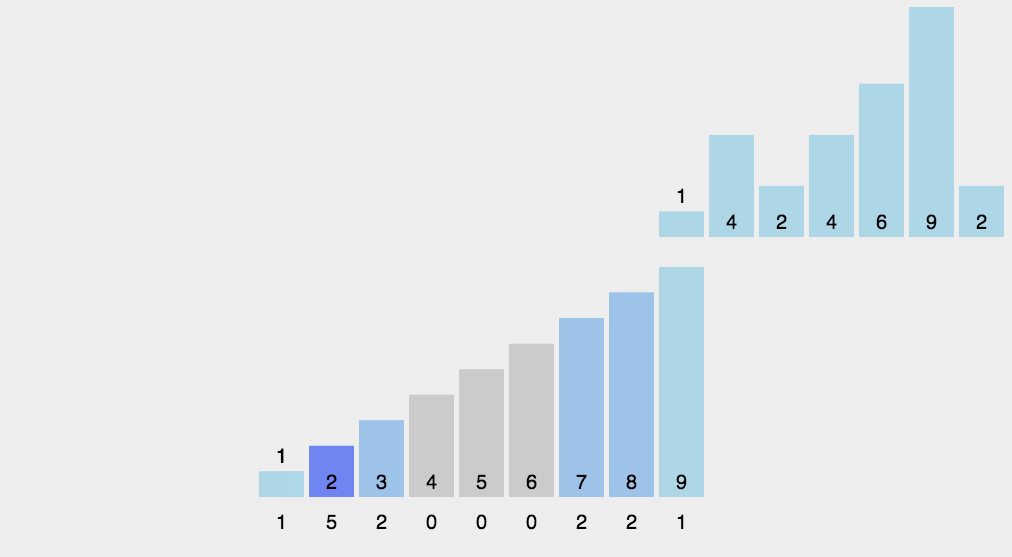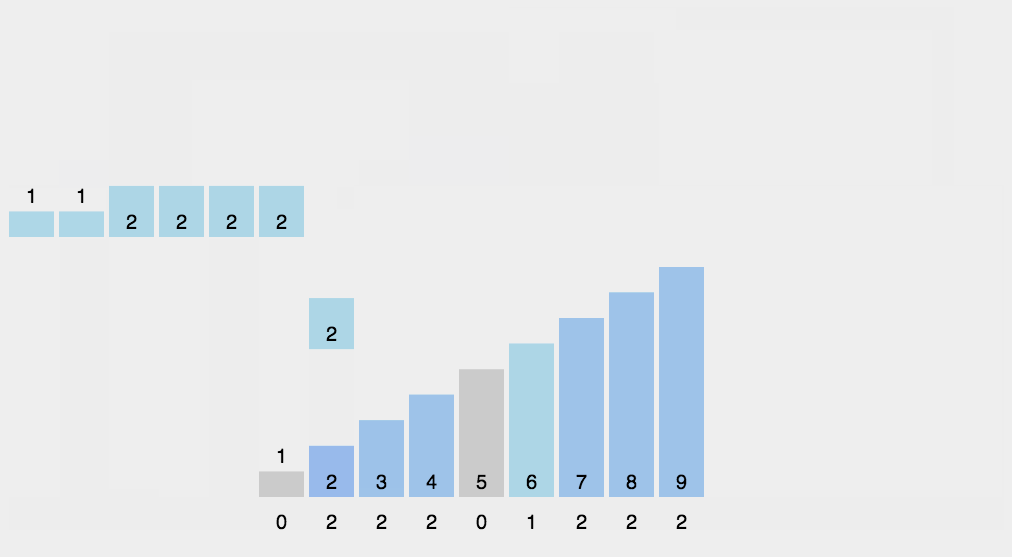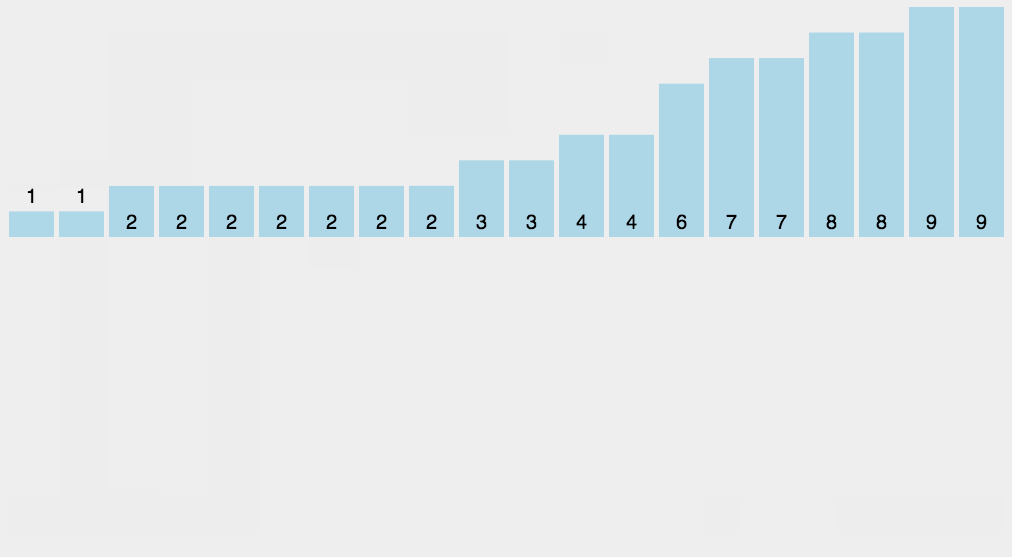[알고리즘] 계수 정렬 Counting Sort

    각 숫자가 몇개 있는지 개수를 세어 저장한 후에 정렬

• 비교(comparison) 정렬의 한계는 O(nlogn)
  => 계수 정렬은 non-comparison sort로 이 한계를 넘어설 수 있다.
• 안정 정렬(stable)
• 최대값이 임시 배열의 크기가 되므로, 숫자 크기에 큰 영향을 받는다. (주어진 숫자에 따라 비효율적일 수 있음)
  

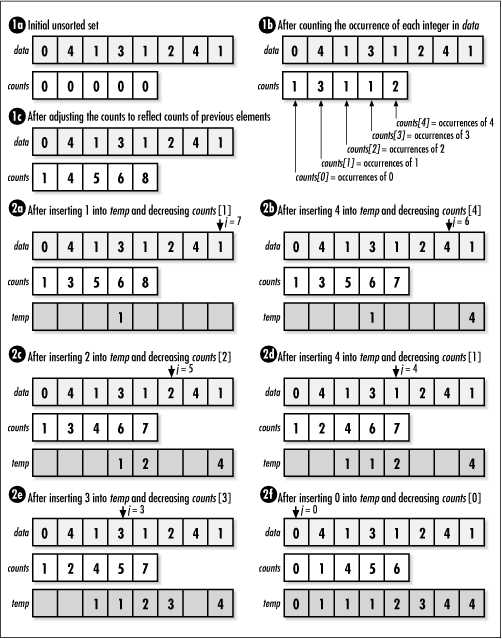
1.
a. 정렬하고자 하는 배열(data)의 최대값을 크기로 하는 임시 배열(counts)을 만든다.
b. 각 원소를 순회하며, 해당 값이 몇개인지를 임시배열에 저장한다.
c. 등장 횟수를 누적합으로 바꾼다.
2.
a. data를 뒤에서 앞으로 순회하면서 temp에 넣어준다. 1c에서 구한 누적합(counts[i])이 숫자의 위치를 알려준다.
b. counts[i]의 값을 하나 줄인다.

이 과정을 반복한다.

• 코드

#include <iostream>

using namespace std;
int arr[1000] = { 10,23,1,1,23,23,4,5,6,7 };
int a[1000];
void counting_sort(int list[])
{
	int temp[1000];
	int count[1000];
	memset(temp, 0, sizeof(temp));
	//더해주기
	for (int i = 0; i < 10; i++)
		temp[list[i]]++;
	count[0] = temp[0];
	//누적으로 더해주기
	for (int i = 1; i <= 23; i++)
		count[i] = count[i - 1] + temp[i];
	//더해졌는지 확인
	for (int i = 0; i <= 23; i++)
		cout << count[i] << " ";
	cout << endl;
	//제일 끝에서 부터 삽입
	for (int i = 9; i >= 0; i--)
	{
		a[  count[ list[i] ]-1 ] = list[i];
		count[list[i]]--;
		//들어가는 위치 보기
		for (int j = 0; j < 10; j++)
			cout << a[j] << " ";
		cout << endl;
	}
	//정렬된 행렬
	for (int i = 0; i < 10; i++)
		cout << a[i] << " ";
	cout << endl;
}
int main()
{
	counting_sort(arr);
}

• 시간 복잡도
  n: 데이터 개수, k: 범위(최대값)

  시간복잡도
  최선	Ω(n+k)
  평균	Θ(n+k)
  최악	O(n+k)

  => k가 n보다 작은 수이면 O(n)이 되지만, k가 n보다 매우 큰 수이면 O(무한)이 될 수도 있다. 예를 들어 10개의 숫자를 정렬하는 데, 가장 큰 숫자가 1000이면 O(n^3)

• 공간 복잡도: O(k)

참고링크1
참고링크2
참고링크3