[알고리즘] DAG와 위상정렬

DAG Directed Acyclic Graph 비순환 방향 그래프

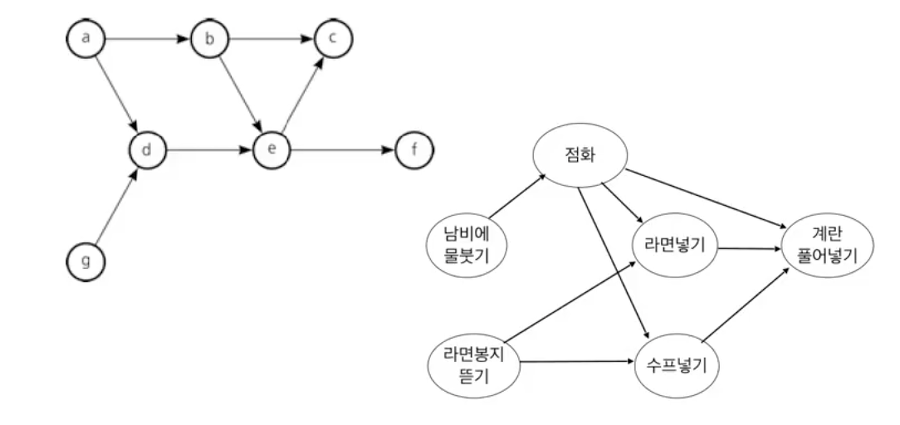    사이클을 가지지 않는 방향그래프

사이클: 자기 자신에서 출발해서 다시 자신에게 돌아오는 경로

• 작업의 우선순위 표현
• 스타크래프트에서 건물 짓는 순서, 대학 과정의 선수과목
• 선행자(predecessor) : DAG에서 어떤 정점 vi∈V, vj∈V에 대해서 vi에서 vj로의 경로가 존재하면, vi를 vj의 선행자(predecessor)라 한다.
• 즉각 선행자(immediate predecessor) : DAG에서 어떤 정점 vi∈V, vj∈V에 대해서 vi에서 vj로의 간선이 존재하면, vi를 vj의 선행자(predecessor)라 한다.
• 후행자(sucessor) : DAG에서 어떤 정점 vi∈V, vj∈V에 대해서 vi에서 vj로의 경로가 존재하면, vj를 vi의 후행자(sucessor)라 한다.
• 즉각 후행자(immediate sucessor) : DAG에서 어떤 정점 vi∈V, vj∈V에 대해서 vi에서 vj로의 간선이 존재하면, vj를 vi의 후행자(sucessor)라 한다.

위상정렬 Topological Sort

    DAG에서 그래프의 방향성을 거스르지 않고 정점들을 나열한 것

• 각 정점을 우선순위에 따라 배치
• 하나의 방향 그래프에는 여러 위상 정렬이 가능
• 노드의 순서가 왼쪽에서 오른쪽 방향으로 향해야 함
• 순서
  

  1. 진입 차수(indgree)가 0인 정점(즉, 들어오는 간선의 수가 0)을 선택
     =>진입 차수가 0인 정점이 여러 개 존재할 경우 어느 정점을 선택해도 무방
  2. 초기에 간선의 수가 0인 모든 정점을 큐에 삽입
  3. 선택된 정점과 여기에 부속된 모든 간선을 삭제
  4. 선택된 정점을 큐에서 삭제
  5. 선택된 정점에 부속된 모든 간선에 대해 간선의 수를 감소

  위의 과정을 반복해서 모든 정점이 선택, 삭제되면 알고리즘 종료

참고링크1
참고링크2