[알고리즘] 최단 경로 문제

💡 최단 경로 문제

    두 노드를 잇는 가장 짧은 경로를 찾거나, 가중치가 있는 그래프(Weighted Graph)에서 간선의 가중치의 합이 최소가 되도록 하는 경로를 찾으려는 것이 목적

• 단일 출발(single-source) 최단경로: 단일 노드 v에서 출발하여 그래프 내의 모든 다른 노드에 도착하는 가장 짧은 경로를 찾는 문제
• 단일 도착(single-destination) 최단경로: 모든 노드들로부터 출발하여 그래프 내의 한 단일 노드 v로 도착하는 가장 짧은 경로를 찾는 문제. 그래프 내의 노드들을 거꾸로 뒤집으면 단일 출발 최단경로문제와 동일
• 단일 쌍(single-pair) 최단 경로: 주어진 꼭지점 u와 v에 대해 u에서 v까지의 최단 경로를 찾는 문제
• 전체 쌍(all-pair) 최단 경로: 그래프 내 모든 노드 쌍들 사이의 최단 경로를 찾는 문제

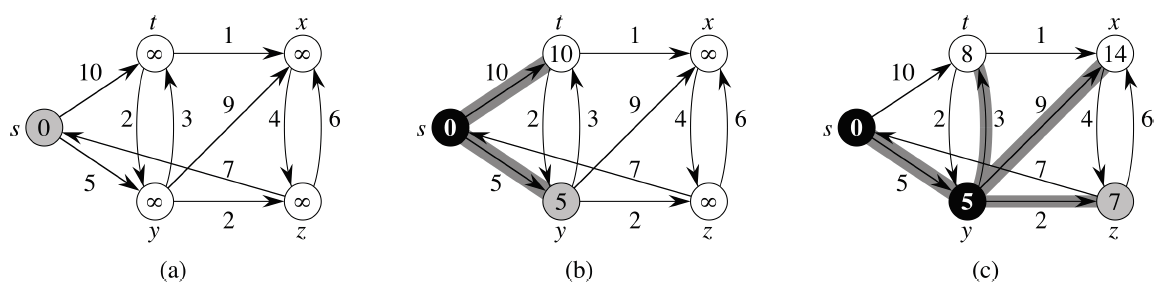
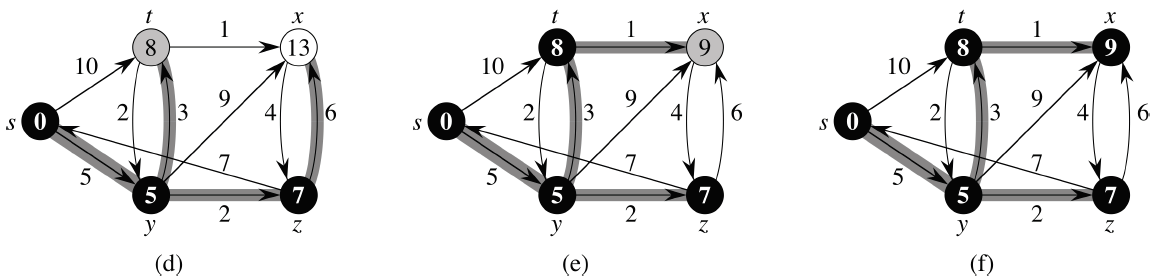
💡 다익스트라 알고리즘 Dijkstra Algorithm

    V개의 정점과 음수가 아닌 E개의 간선을 가진 그래프 G에서 특정 출발 정점(S)에서부터 다른 모든 정점까지의 최단경로를 구하는 알고리즘.

• 음이 아닌 가중 그래프에서의 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제
• 각 정점을 최대 한 번씩만 방문하여 최단 거리 확정(음의 가중치 불가)
• 아직 방문하지 않은 정점들 중 최단거리인 점을 찾아 방문하여 최단거리를 확정하고, 이를 반복

BFS 기반
1. 시작노드를 제외한 모든 노드의 거리정보를 무한대로 초기화한다.
2. 아직 방문하지 않은 정점들 중 거리가 가장 짧은 정점을 하나 선택해 방문한다.
3. 해당 정점에서 인접하고 아직 방문하지 않은 정점들의 거리를 갱신한다.

• 시간복잡도: O(ElogV)

참고링크1
참고링크2

// 개선된 다익스트라 알고리즘 추가(최소 힙, 우선순위 큐)

💡 벨만-포드 알고리즘 Bellman-Ford-Moore Algorithm

    시작노드 s에서 v에 이르는 최단경로를 s에서 u까지의 최단경로에 u에서 v 사이의 가중치(거리)를 더한 값으로 분해(decomposition)한다. 그래프에서 시작 정점에서 특정 정점까지 도달하기 위해 거쳐가는 최대 간선 수는 V−1개 이기 때문에 edge relaxation을 V-1번 수행한다.

• 가중 그래프에서 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제
• 음의 가중치를 가지는 간선도 가능
• 음의 사이클의 존재 여부 확인 가능
  => V번째 모든 간선을 확인했을 때 거리배열이 갱신된다면 음의 사이클을 가지는 그래프

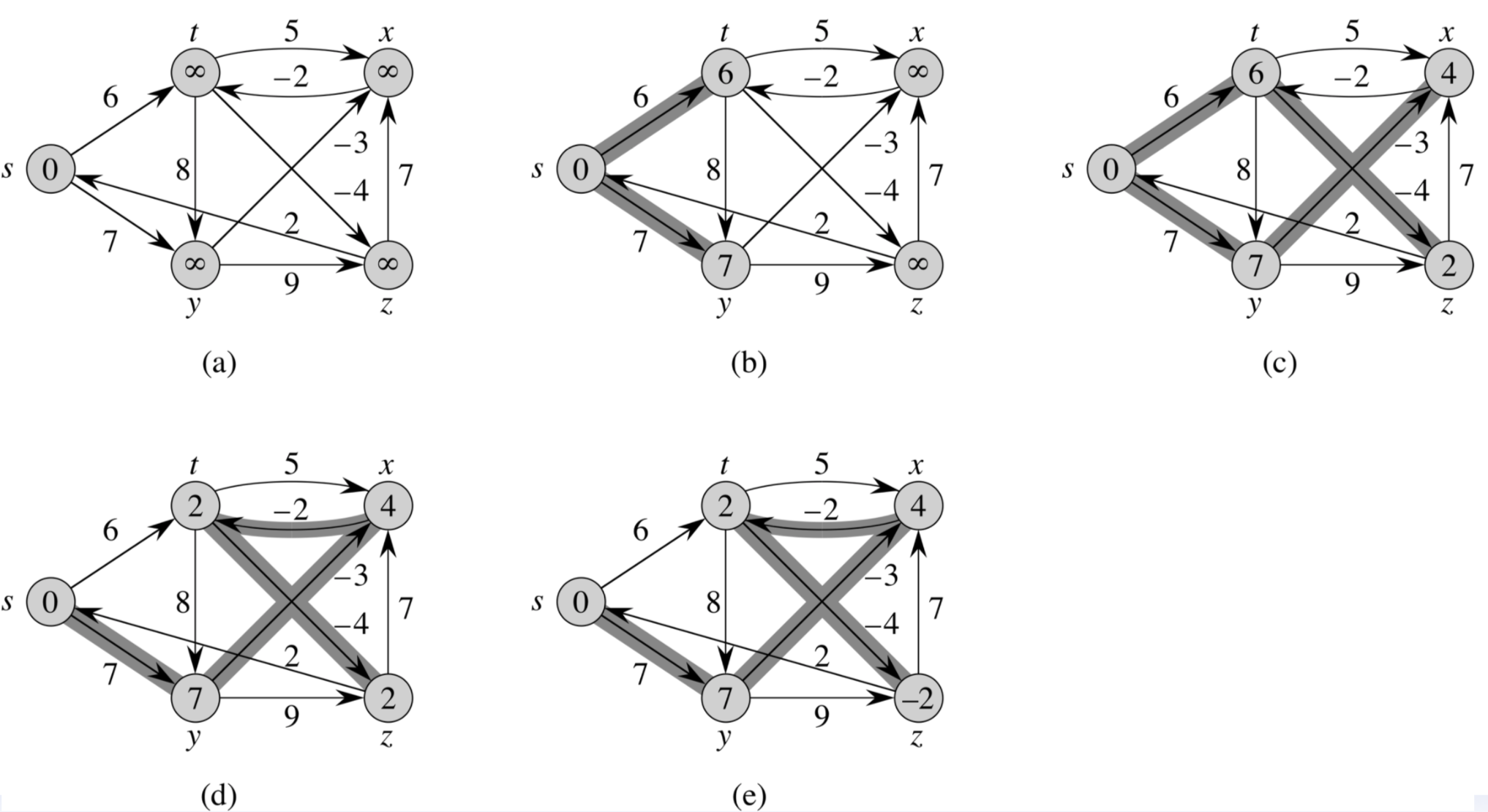
1. 시작 정점을 결정한다.
2. 시작 정점부터 다른 정점까지 거리 값 모두 무한대로 초기화한다. (시작 정점은 0으로 초기화)
3. 현재 정점의 모든 인접 정점들을 탐색하며, 기존에 기록된 인접 정점까지의 거리보다 현재 정점을 거쳐 인접 정점에 도달하는 거리가 더 짧다면 인접 정점까지의 거리를 갱신한다.

3번 과정을 V−1번 반복한다.
위 과정을 모두 마친 후에도 거리가 갱신되는 경우가 있다면 그래프에 음수 사이클이 존재한다는 것을 알 수 있다.

• 시간복잡도: O(EV)

참고링크1
참고링크2

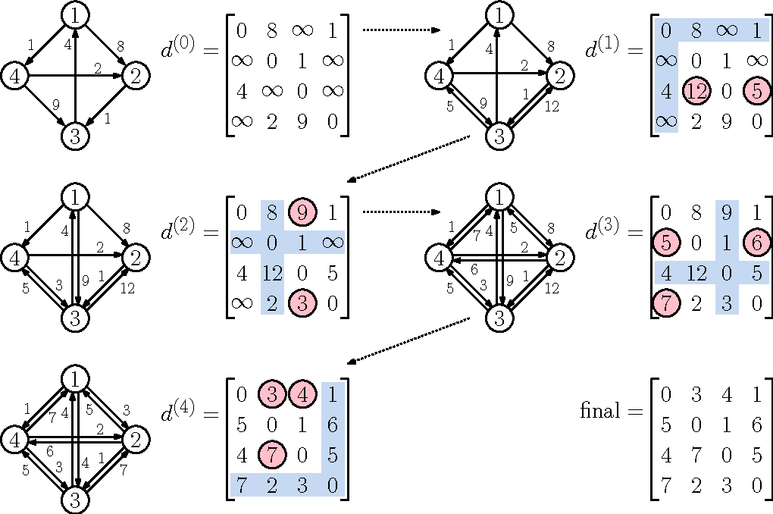
💡 플로이드-워셜 알고리즘 Floyd-Warshall Algorithm

    V개의 정점과 E개의 간선을 가진 가중 그래프 G에서 모든 정점 사이의 최단경로를 구하는 알고리즘. 어떤 두 정점 사이의 최단 경로는 어떤 경유지 K를 거치거나 거치지 않는 두 가지이기에 A-B이거나 A-K-B이다. 만약 경유지 K를 거친다면, 최단 경로를 이루는 부분 경로 A-K와 K-B도 각각 최단 경로이다.

• 전체 쌍 최단 경로 문제에 자주 쓰임
• 순환만 없다면 음수 가중치도 가능
• 동적계획법으로 접근
• $D[i][j]=D[i][k]+D[k][j]$
  => 현재까지 계산된 정점 i에서 j로 가는 시간보다 정점 k를 거쳐서 가는 길이 더 작다면 교체

• 시간복잡도: O(V^3)