[알고리즘] 최소 공통 조상 LCA

💡 최소 공통 조상 LCA(Lowest Common Ancestor)란?

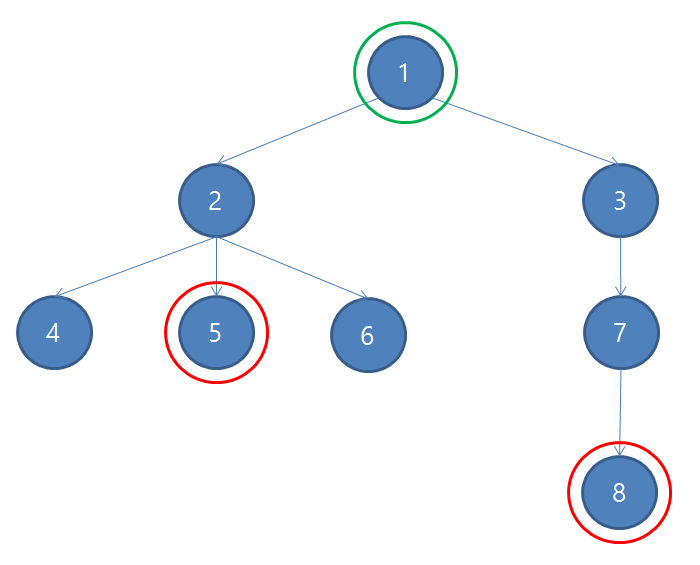    정점 A와 정점 B가 각각 자신을 포함하여 조상을 따라 거슬러 올라 갈 때 처음 공통으로 만나게 되는 정점으로, 정점 A 혹은 A의 조상이면서 정점 B 혹은 B의 조상인 정점들 중 가장 깊은 정점

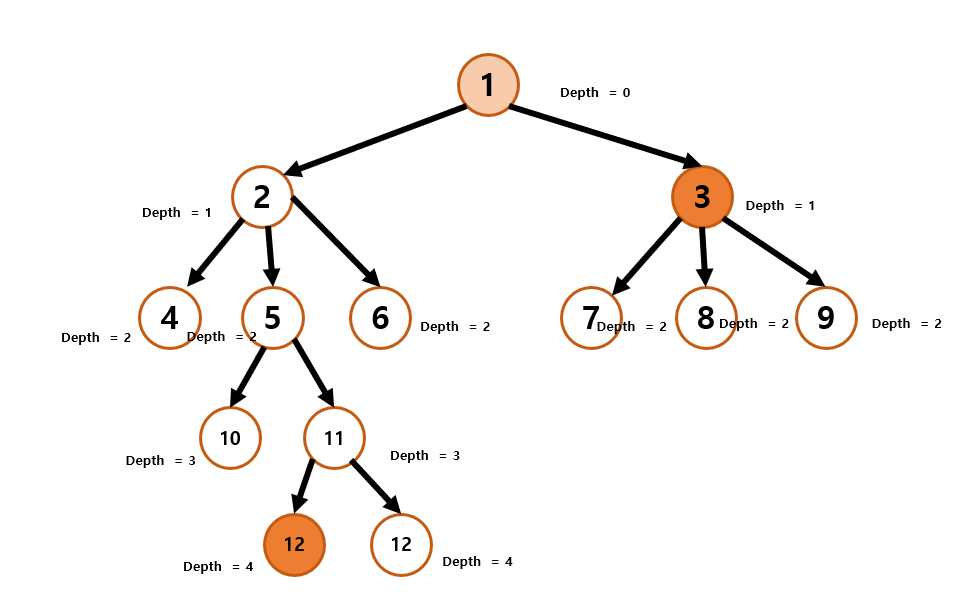
1. 최상위 조상 정점을 시작으로 DFS(또는 BFS)를 수행하여 각 정점의 깊이(depth)와 부모 정점을 저장한다.
2. LCA를 구하려는 두 노드 중 더 깊은 노드의 depth를 더 낮은 노드의 depth로 맞춘다.
   =>사진에서 노드 12의 depth가 4, 노드 3의 depth가 1이므로, 노드 4를 depth가 1이 될 때 까지 부모를 찾으며 올려준다.
3. 이후 두 노드를 같이 한칸씩 parent를 찾아가며 동일한 부모(LCA)가 나올 때 까지 찾는다.

• 시간복잡도: O(logN)이지만, 최악의 경우 O(N)(사향이진트리)

더 빠른 방법
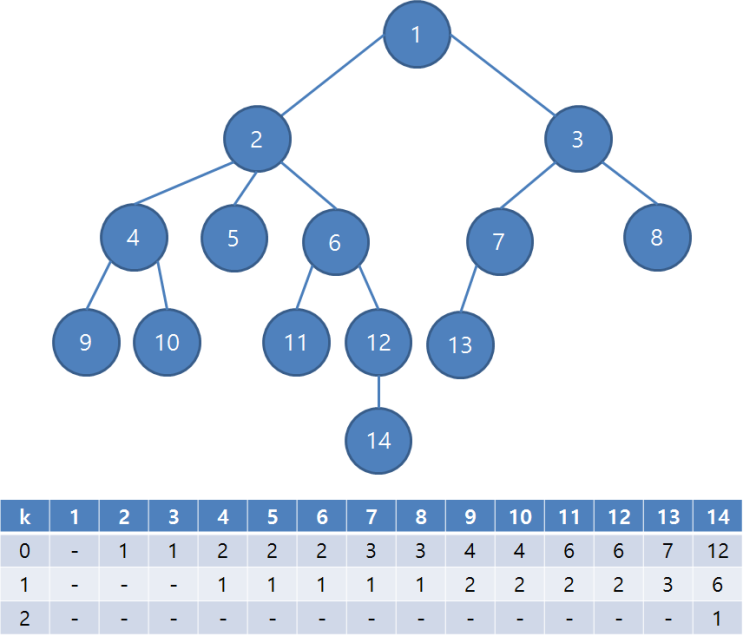
과거 1번 과정에서 각 정점의 부모 뿐 아니라 2k번째 조상까지 저장
parent[K][V]: 정점 V의 k번째 조상
=> parent[K][V] = parent[k-1]parent[k-1][V]]

두 정점 u, v가 있고 depth[u]>=depth[v]일 때,
1. depth[u] > depth[v]일 때, u와 parent[u]로 대체하는 것을 반복한다.

 for(int j = 0; diff != 0; j++){
 	if( diff%2 != 0){
    	num1 = parent[num1-1][j]+1;
    }
    diff /= 2;
 }

=>두 정점의 깊이 차이 diff(depth[u]-depth[v])를 이진수로 바꾸는 과정. 깊이가 많이 날 때, 부모를 하나씩 따라 갈 필요는 없다. 만약 둘의 깊이 차이가 11이라면 이것은 이진수로 1011(2)이므로, 2^0번째 부모->2^1번째 부모->2^3번째 부모를 따라 가면 됨.
2. u != v 일 때, u를 parent[u], v를 parent[v]로 동시에 대체하는 것을 반복한다.

if(num1 != num2){
            for(int j=(int)MAX-1; j>=0; j--){
                if((parent[num1-1][j] != -1) && (parent[num1-1][j] != parent[num2-1][j])){
                    num1 = parent[num1-1][j]+1;
                    num2 = parent[num2-1][j]+1;
                }
            }
            num1 = parent[num1-1][0]+1;
        }

참고링크-이진수 변환
참고링크2