 힙(Heap) 자료구조를 기반으로 한 정렬방식
힙(Heap) 자료구조를 기반으로 한 정렬방식
- 정렬해야 할 n개의 요소를 최대 또는 최소 힙을 구성한다. (완전 이진 트리 형태)
- 현재 힙의 root에는 최대 or 최소값. 루트의 값을 마지막 요소(말단 노드)와 바꾼 후에, 힙의 사이즈를 하나 줄인다.
=> 최대 혹은 최소값을 하나 뽑을 수 있다.- 힙의 사이즈가 1보다 크면 이 과정을 반복
힙 Heap
힙 조건을 만족한는 완전 이진 트리(Complete Binary Tree)형태의 자료구조로 우선순위 큐를 위해 만들어졌다.완전 이진 트리 Complete Binary Tree
각 노드의 자식 수가 2 이하인 트리(이진 트리)로, 마지막 레벨은 노드가 왼쪽에 몰려있고 마지막 레벨을 제외하면 모든 단말 노드의 깊이가 같다.힙 조건
- 노드의 키 값은 자식 노드의 키 값보다 항상 크다 (최대힙 Max Heap)
- 노드의 키 값은 자식 노드의 키 값보다 항상 작다 (최소힙 Min Heap)
=> 주어진 데이터를 힙 조건을 만족하게 만드는 것을 Heapify라 함
- 불안정 정렬(unstable)
- 내림차순 정렬을 위해서는 최대 힙, 오름차순 정렬을 위해서는 최소 힙을 구성
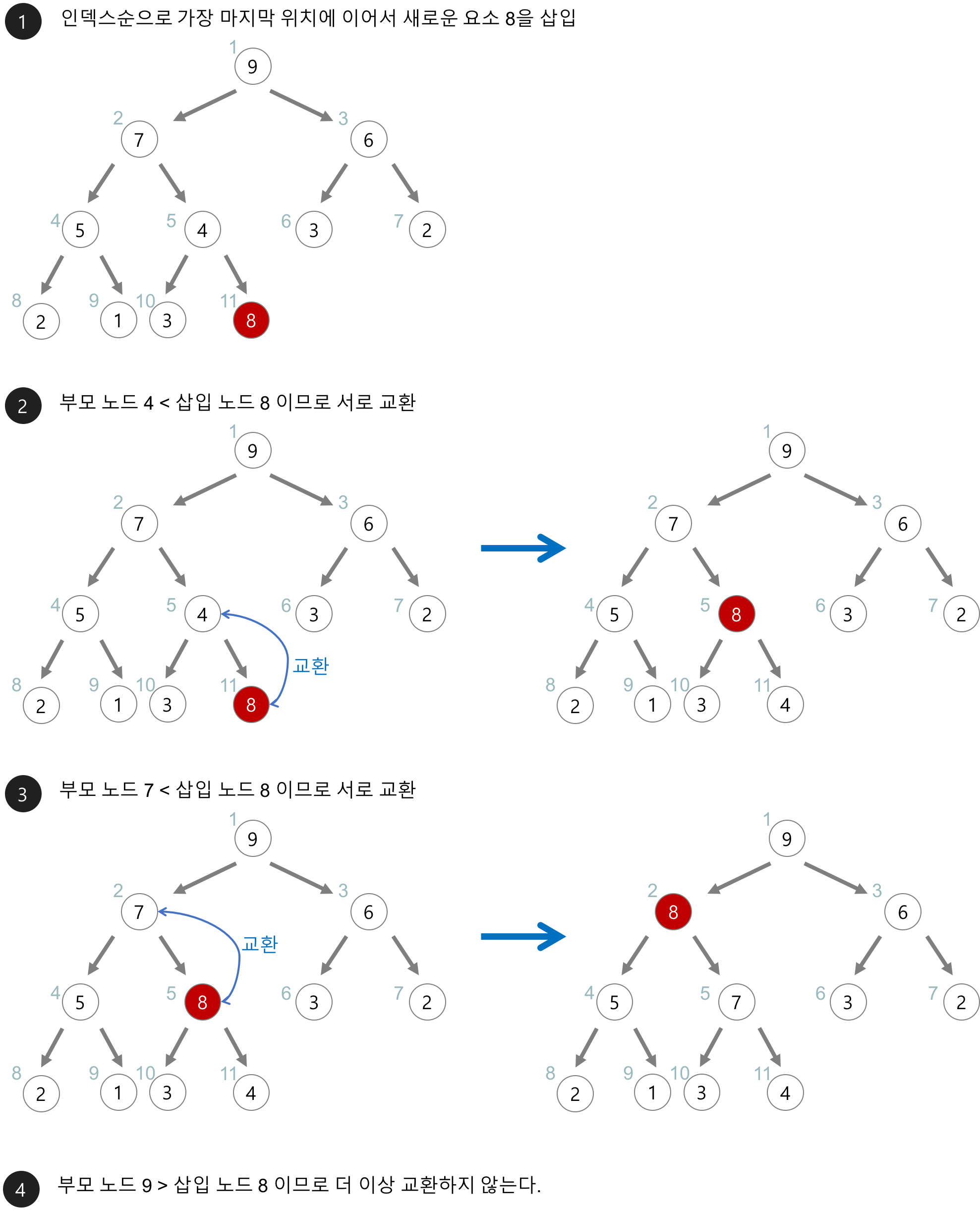
- 최대 힙(Max Heap)의 삽입
- 힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입
- 새로운 노드를 부모 노드들과 교환해서 힙의 성질을 만족시킴
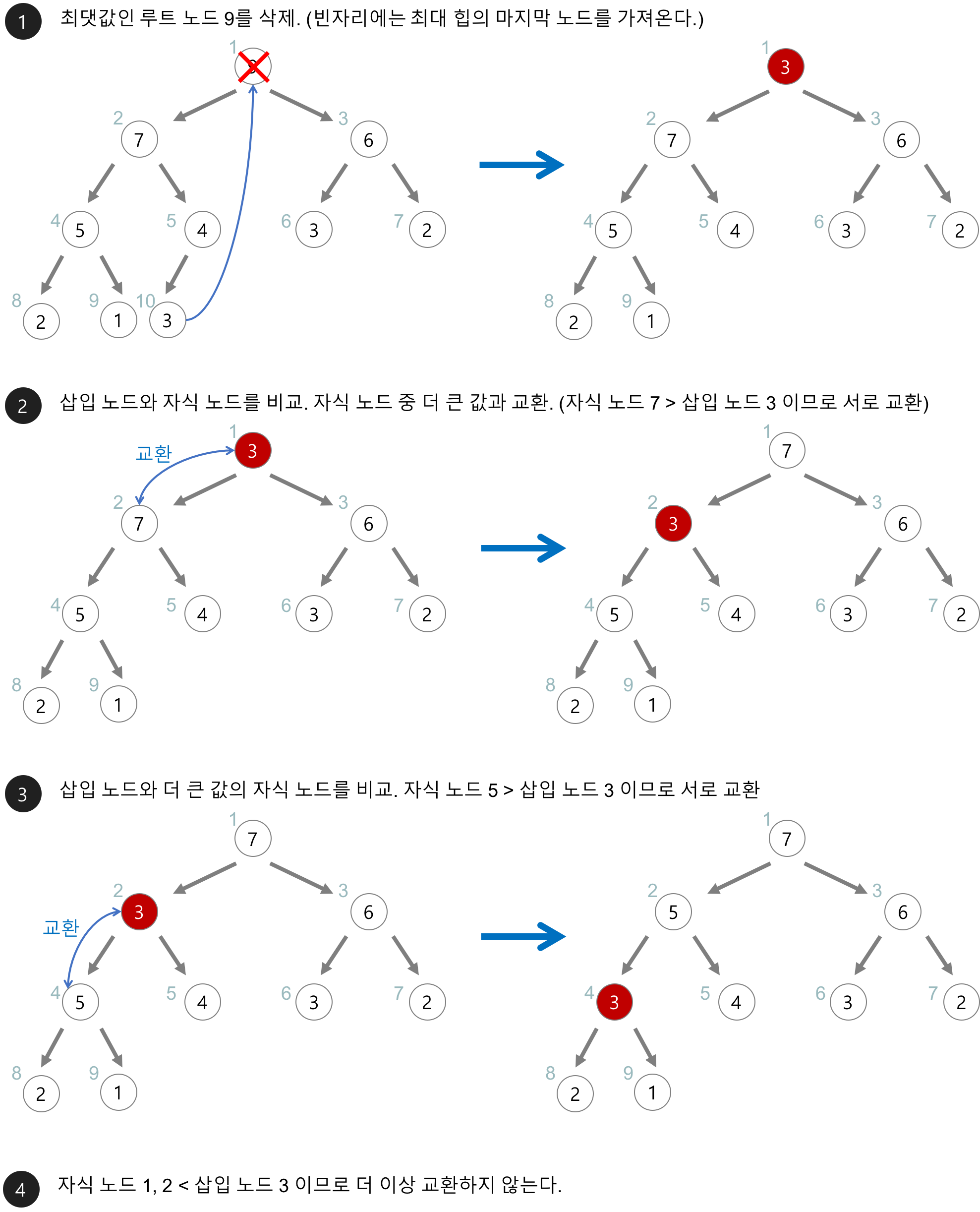
- 최대 힙(Max Heap)의 삭제
- 최대 힙에서 최댓값은 루트 노드이므로 루트 노드가 삭제
=> 최대 힙(max heap)에서 삭제 연산은 최댓값을 가진 요소를 삭제하는 것이다. - 삭제된 루트 노드에는 힙의 마지막 노드를 가져옴
- 힙을 재구성
- 최대 힙에서 최댓값은 루트 노드이므로 루트 노드가 삭제
- 코드
배열에 트리 노드를 레벨 순서대로 왼쪽에서 오른쪽으로 저장하고, 배열의 1번부터 저장을 시작할 때
i번 노드의 부모 노드:i/2
i번 노드의 왼쪽 자식:i*2
i번 노드의 오른쪽 자식:i*2+1
#include <iostream>
using namespace std;
int n, heap[10000001];
void heapify(int i)
{
int cur = 2 * i;
if(cur < n && heap[cur] < heap[cur+1]) cur++;
if(heap[i] < heap[cur])
{
swap(heap[i],heap[cur]);
if(cur <= n/2) heapify(cur);
}
}
void heapsort(int i)
{
swap(heap[1],heap[i]);
int root = 1;
int cur = 2;
while(cur/2<i)
{
cur = 2*root;
if(cur < i-1 && heap[cur] < heap[cur+1]) cur++;
if(cur < i && heap[root] < heap[cur])
swap(heap[root],heap[cur]);
root = cur;
}
}
int main()
{
scanf("%d",&n);
for(int i = 1; i <= n; i++)
scanf("%d",&heap[i]);
for(int i = n/2; i > 0; i--) // 최초 heap 생성
heapify(i);
for(int i = n; i > 0; i--) // heap 정렬
heapsort(i);
for(int j = 1; j <= n; j++) // 출력
printf("%d ",heap[j]);
}-
시간복잡도
시간복잡도 최선 Ω(nlogn) 평균 Θ(nlogn) 최악 O(nlogn) 힙 트리의 전체 높이가 거의
log₂n(완전 이진 트리이므로)이므로 하나의 요소를 힙에 삽입하거나 삭제할 때 힙을 재정비하는 시간이log₂n만큼 소요된다.
요소의 개수가n개 이므로 전체적으로O(nlog₂n)의 시간이 걸린다.
T(n) = O(nlog₂n) -
공간복잡도:
O(1)
