백준 12015 가장 긴 부분 증가 수열 2

• 문제 링크
  가장 긴 증가하는 부분 수열
  가장 긴 부분 증가 수열 2

이번 문제를 풀 때는 원래 아래와 같은 방법을 사용했었습니다.
i번째 지점 이전을 모두 탐색하여 i번째 수보다 작은 수들 중 카운트 횟수가 가장 큰 수에 +1 을 하여 기록해놓는 방식이었습니다.

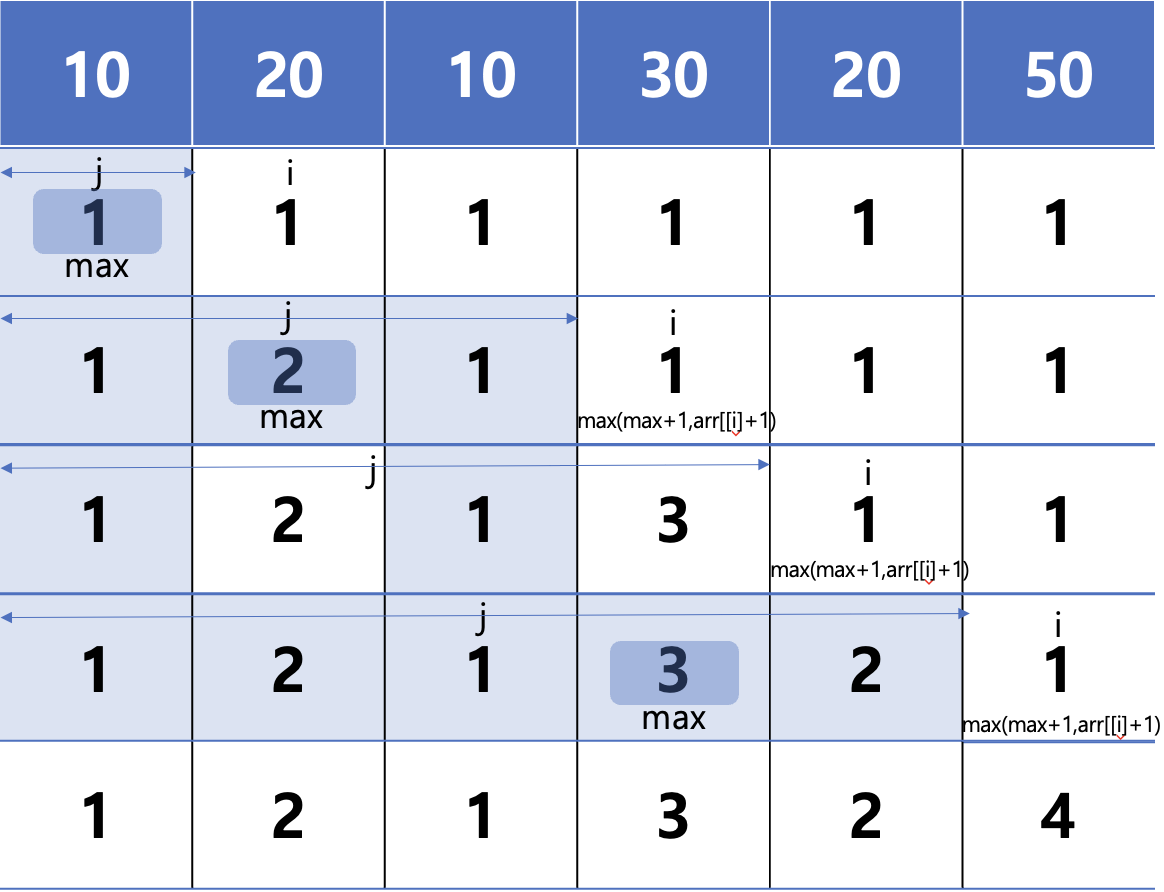
하지만 이러한 방식은 지금 문제와 같이 $10^6$크기의 입력이 주어졌을 때, 난처해지게 됩니다. 왜냐하면 위 그림처럼 j범위의 탐색은 $1+2+ ... + n-1 =\frac{n(n-1)}{2}$번, 즉 $O(n^2)$의 시간복잡도를 가지기 때문입니다.

어떻게 풀어야할지 감이 잘 잡히지 않아 답지를 보게되었습니다.
아이디어는 list에 원소를 하나씩 추가해나가는 것인데 아래와 같습니다.

• list의 top이 새로 들어올 원소보다 작다면 append()
• 만일 크다면 현재 list에서 원소가 들어갈 위치를 찾아 바꿔 넣습니다. 전체 list길이는 유지한 채 말이죠. 이 때 이분 탐색을 활용하여 시간 복잡도를 줄일 수 있습니다.

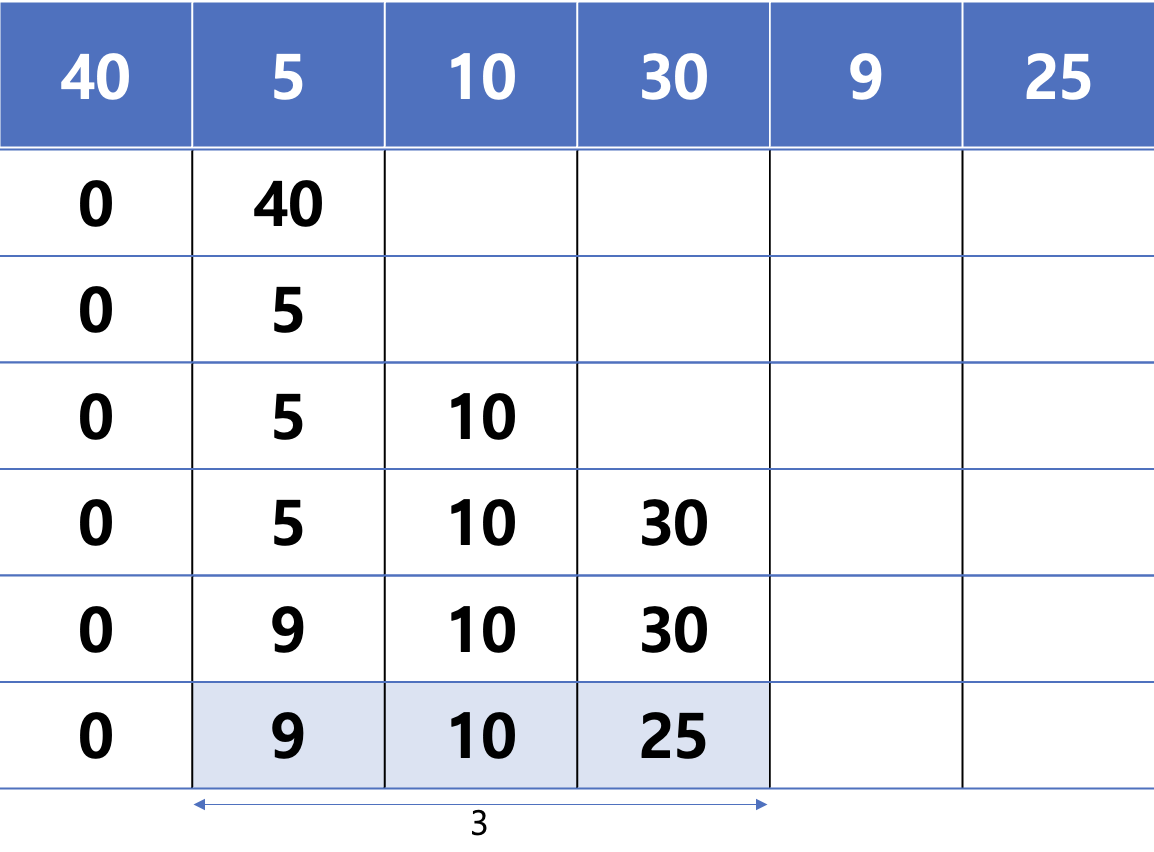
이처럼 원소를 넣어야할 때, 넣을 위치를 탐색해서 바꿔 낍니다. 하지만 최종적으로 나온 저 원소들은 실제 답 [5,10,30(25)]과는 다른 것을 알 수 있습니다. 이는 수열이 늘어날 때를 확인만 하면 되기 때문입니다.

def sol():
    memo = [0]

    for elem in arr:
        if elem > memo[-1] : memo.append(elem)
        else : # 들어가서 바꿀 자리 찾음
            left = 0
            right = len(memo) # 탐색 길이 만큼

            while left < right:
                mid = (left+right) // 2

                if memo[mid] < elem:
                    left = mid + 1
                else :
                    right = mid # 탐색 길이 만큼
            memo[right] = elem
    
    return len(memo) -1

## input
N = int(input())
arr = list(map(int,input().split()))
## output
print(sol())