우리가 평소 알던 식은 중위 표기식입니다. 이를 후위 표기식으로 변환을 해야하는 문제입니다. 우선순위가 높은 연산자를 먼저 연산할 것이기 때문에, 높은 연산자를 바로 뒤 피연산자 뒤로 빼주는 일입니다. 아래처럼 말이죠
- 3 + 8 * 9 -> 3 + (89 *) -> 389 * +
이와 같은 표기식으로 변환하려면 어떤 자료구조를 활용해볼 수 있을까요??
바로 Stack입니다!
stack의 FIFO(First In First Out)성질을 이용해 연산자의 우선순위에 따라 적절히 넣고 빼주면 후위 표기식으로 변환할 수 있습니다.
주어진 중위 표기식의 문자를 하나씩 탐색해 나가며 후위표기식으로 바꿔주는 것입니다. 여기서 stack에 언제 원소를 넣고 빼줄지 그 전략을 생각해봐야 합니다.
알고리즘
앞서 말한 내용에 대한 알고리즘을 정리해보면, 아래와 같습니다.
- 탐색한 문자가 피연산자이면, 그대로 기록합니다.
- 탐색한 문자가 연산자일 때,
1. 만약 stack이 비어있다면, 그대로 stack에 넣어줍니다.
2. stack의 top이 현재 탐색한 연산자보다 우선순위가 높으면, stack내 존재하는 원소 모두, 혹은 '('를 만날 때까지 모두 빼줍니다. 그리고 탐색한 원소를 stack에 추가합니다. 우선순위가 같을 땐 top을 빼주고 탐색한 연산자를 넣으면 됩니다.
3. stack의 top이 현재 탐색한 연산자보다 우선순위가 낮다면, 탐색한 원소를 stack에 추가합니다.- 탐색한 문자로 괄호( '(' 또는 ')' )를 만났을 때,
1. '(' 이면 stack에 추가합니다.
2. ')' 이면 '('를 만날 때 까지 stack내 원소들을 빼줍니다.- 마지막에 도착했다면, stack에 모든 원소를 빼줍니다.
예시를 통해 어떻게 적용되는지 보면 좋을 것 같습니다.
- A*B+C -> AB*C+
stack은 + 를 만났을 때 stack의 top보다 낮은 연산자를 만나므로, 다음처럼 변합니다. : [ * ] -> [ + ] ( * : pop)
- A+B+C -> AB+C+
stack은 동등한 연산자를 만나며 기존의 +가 나오고 새로운 +가 들어오며 마지막에 추가되는 것을 볼 수 있습니다.
- A+B*C÷D -> ABC*D÷+
stack은 *를 만날 때까지 연산자들을 push하다가, / 를 만날 때 아래처럼 변합니다. 이는 우선순위가 동등한 연산자를 만난 것이기에 이처럼 수행되는 것이죠 :)
[ +, * ] -> [ +, ÷ ] ( * : pop)
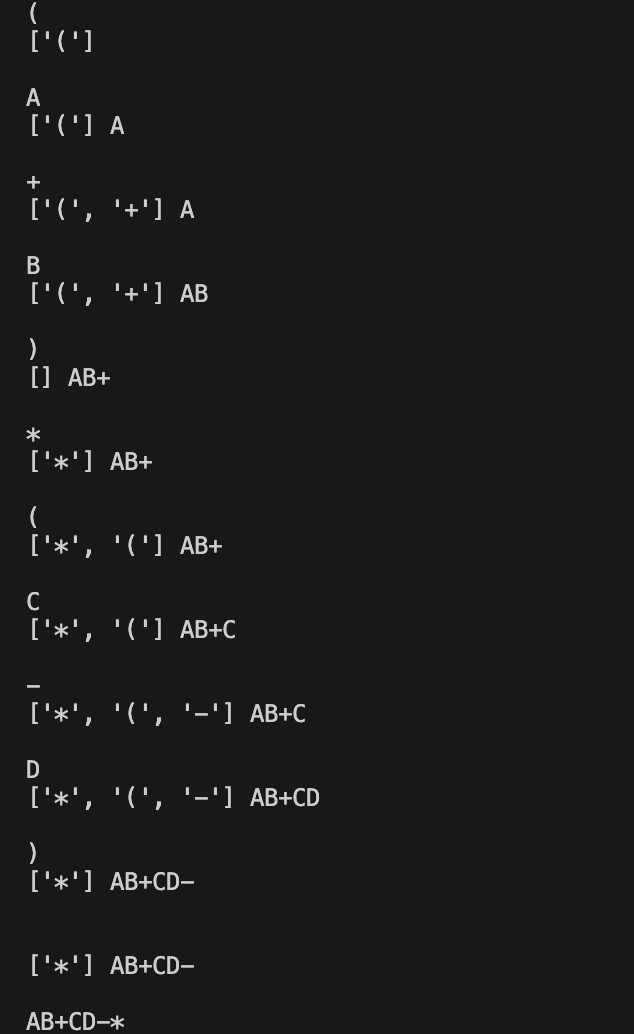
- (A+B)*(C-D)
괄호가 포함된 경우는 ')'를 만나기 전까지 동일하게 진행하다가, ')'를 만나면 '(' 앞까지의 연산자를 pop해줍니다.
아래 그림은 현재 문자와 stack의 상황, 그리고 최종출력이 만들어지는 모습입니다.
괄호가 없었다면 좀 더 간결해질 수 있겠으나, 주어지는 수식에 괄호가 포함되어있어 어떻게 괄호의 내용까지 처리할 수 있는 통일성있는 로직을 만들지 많이 고민하게 됬던 문제였습니다.
method
## method
def sol(expr):
leng = len(expr)
oper_stack = []
answer = ''
for i in range(leng):
if expr[i].isalpha(): answer += expr[i]
else : # expr[i] 가 +,-,*,/,(,)
if expr[i] == '(': oper_stack.append(expr[i])
elif expr[i] in ('*','/'): # stack top이 + - 이면 추가할 수 있음 * / 이면(우선 순위 같으면) 뺴내야 함.
while oper_stack and oper_stack[-1] in ('*','/'):
answer += oper_stack.pop()
oper_stack.append(expr[i])
elif expr[i] in ('+','-'): # 스텍 내 연산자들보다 우선순위가 무조건 같거나 작기 때문에 무조건 뺴낼 예정
while oper_stack and oper_stack[-1] != '(': #스텍 내 연산자들을 다 빼내야함. ( 존재한다면 ( 전까지
answer += oper_stack.pop()
oper_stack.append(expr[i])
elif expr[i] == ')':
while oper_stack and oper_stack[-1] != '(': #( 존재한다면 ( 전까지 스텍 내 연산자들을 다 빼냄. 마지막 ( 도 pop
answer += oper_stack.pop()
oper_stack.pop()
while oper_stack:
answer += oper_stack.pop()
return answer
## input
expr = input()
## output
print(sol(expr))