• 문제 링크

sol

입력이 10¹⁸ 인 것을 감안해보면 흔히 알던 dp식 풀이로는 시간초과가 뜰 것이 분명했습니다. 다른 방식을 고민해봐야 했죠..

피보나치 수 식은 문제에서도 제시가 되었듯이 아래와 같죠.

Fn = Fn-1 + Fn-2 (n ≥ 2)

이 식에서 또다른 규칙은 없나 하고 좀 뜯어봤습니다.

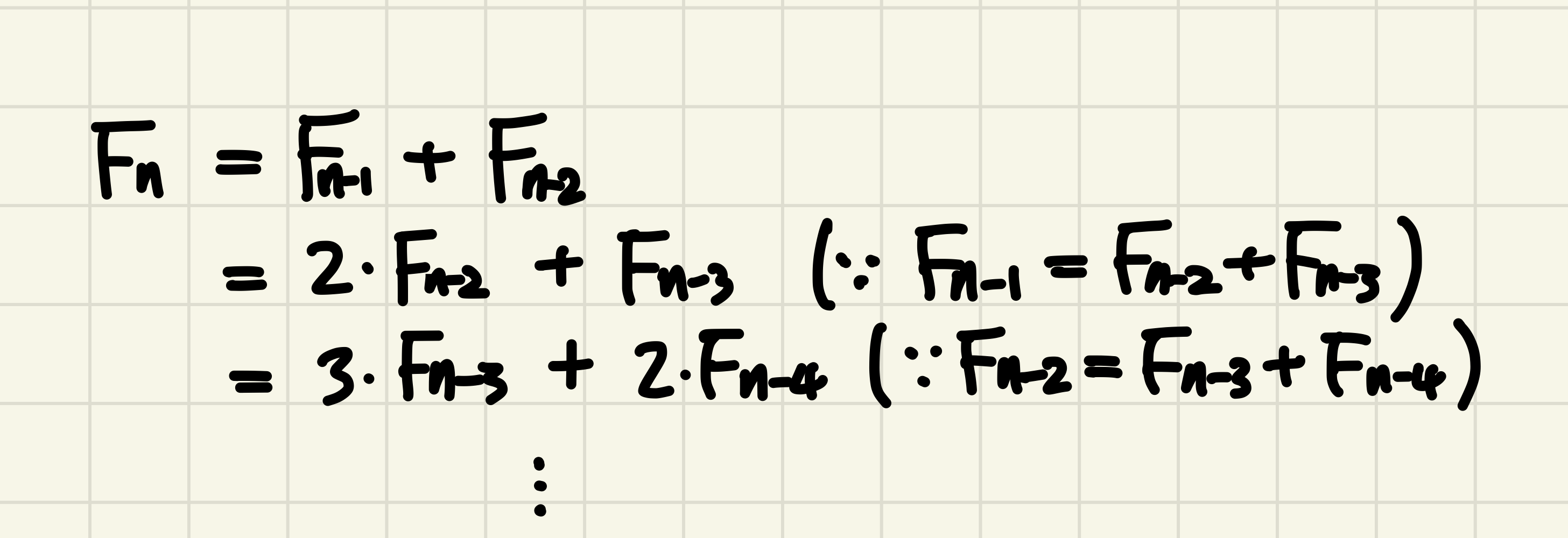
잘 보이실까 모르겠네요 ㅎㅎ.. 글씨에 소질 없는 편입니다 ㅋㅋ
근데 이 식을 이렇게도 볼 수 있더라구요.

즉 또다른 피보나치 곱의 합으로 나타내는게 가능했습니다.

주어진 입력값의 범위가 크니, n을 절반으로 쪼갠 n/2로 나타내어 보았었는데요. n이 홀수일 때와, 짝수일 때가 점화식이 다르게 나오더군요.

여기까지는 유도 과정이었으니, 최종식은 제 글씨 말고 컴퓨터 글씨로 표현하자면,

• $\begin{aligned} F_{2n-1} = F_n^2 + F_{n-1}^2\end{aligned}$
• $F_{2n} = (F_{n-1} + F{n+1})F_n = (2F_{n-1} + F_n)F_n$

위와 같은 형태로 점화식이 나왔습니다.

이와 같이 절반씩 쪼개어 나가다보면, 피보나치 값을 아는 F₂이하로 도달할 수 있을 것이고, 따라서 시간복잡도 O(logN)으로 연산을 수행할 수 있을 것 같았습니다.

이를 수행하려면, 재귀를 이용하고 dp알고리즘을 수행할 때처럼 memorization을 수행하면 구현될 것 같았습니다.

method

## method
def F(num):
    if num <= 2:
        return memo[num]
    
    else :
        half = num //2
        if num % 2 == 0 :
            h0 = F(half)
            h1 = F(half-1)
            memo[num] = ((2*h1 + h0)*h0)%1000000007
            return memo[num]
        else : 
            h0 = F(half+1)
            h1 = F(half)
            memo[num] = (h0**2 + h1**2)%1000000007
            return memo[num]
            
## input
from collections import defaultdict
n = int(input())
memo = defaultdict(int)
memo[1],memo[2] = 1,1
## output
print(F(n))

처음엔 이렇게 구현했는데, 엄청 오래결려서 뭘 빠뜨렸나 고민했습니다.

생각해보니, memo한 연산을 계속 중복해서 하고있더라구요. 이렇게 짜면 아무 메리트가 없죠 ㅎㅎ;

처음은 연산을 해서 이를 dictionary를 활용해 기록하고, 이후 다른 재귀함수에서 동일한 연산을 수행할 때 이 해시값을 갖다 쓰도록 했습니다.

결국 divide&conquer와 dp알고리즘을 이용해 푼 문제가 되겠습니다.

## method
def F(num):
    if num <= 2:
        return memo[num]
    # 중복 연산 막음 : 메모 활용
    elif memo[num] > 0:
        return memo[num]
    # 해시값 존재 안할 시 최소 한번은 연산해주어야 함.
    else :
        half = num //2
        if num % 2 == 0 :
            h0 = F(half)
            h1 = F(half-1)
            memo[num] = ((2*h1 + h0)*h0)%1000000007
            return memo[num]
        else : 
            h0 = F(half+1)
            h1 = F(half)
            memo[num] = (h0**2 + h1**2)%1000000007
            return memo[num]
            
## input
from collections import defaultdict
n = int(input())
memo = defaultdict(int)
memo[1],memo[2] = 1,1
## output
print(F(n))