백준 2133 : 타일 채우기 - 파이썬

2xN에 이어 이번엔 3xN의 타일을 채우는 경우를 생각해 보는 것이다.

우선 N=2일 때, 사용할 수 있는 타일로 채울 수 있는 경우의 수는 총 3가지이다.

N=3 (홀수) 일 때, 3xN(홀수)는 애초에 홀수개의 타일을 채워야 하는데, 사용할 수 있는 타일은 2칸짜리만 존재하므로 항상 한칸씩 남을 것이다. 따라서 홀수일 때는 경우의 수가 0이다.

N=4일 때를 고려해보자.

• 이를 앞서 구한 N=2일때로 쪼개보면 2+2의 결합으로 볼 수 있을 것이다.
  각각 3가지 경우이며, 이는 중복될 수 있으므로 3x3가지가 가능하다.
• 또 가능한 경우는 ㄷ자 지붕으로 덮히는 경우! 이때는 위, 아래일 때 총 2가지가 존재하게 된다.
• 결론은 2일때의 조합 2+2와 특수한 경우 2가지의 합이다.

따라서 3x3 + 2 = 11가지일 것이다.

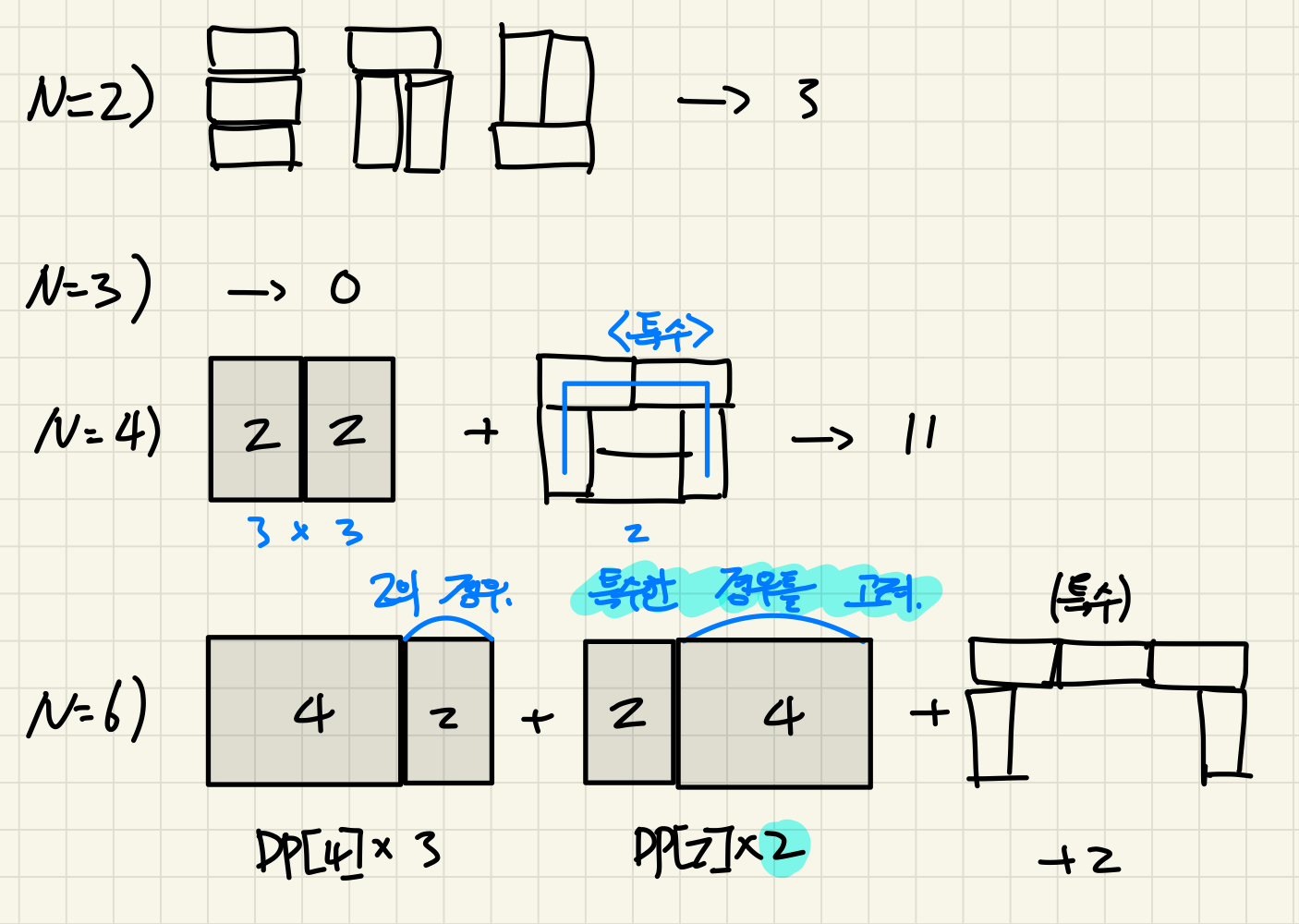
N=6일 때까지 생각을 해보고 규칙을 찾아보도록 하자.

• 먼저 최소단위(2)로 쪼개보면 4+2로 합쳐진 경우로 볼 수 있겠다. 이 때는 4일때 경우와 2일 때 경우를 곱해주면 될 것이다 : dp[4] x 3

이번엔 2+4로 합쳐진 경우이다.
얼핏보면 4+2일때에서 2를 곱하면 되는거 같다가도, 중복되는 경우는 없는지 고려해보게 되었다.

4+2와 2+4일 때 (2+2)+2 와 2+(2+2)처럼 생각을 해보면 2일때의 경우가 중복 되어있다. 다만, 4가 특수한 경우(ㄷ자 지붕)일 때는 고려가 되어있지 않다.
따라서 2+4를 고려할 때는 4가 특수한 경우일 때(2가지)만을 고려하여 곱하면 되는 것!

참고로 N=8일 때는 다음과 같다.

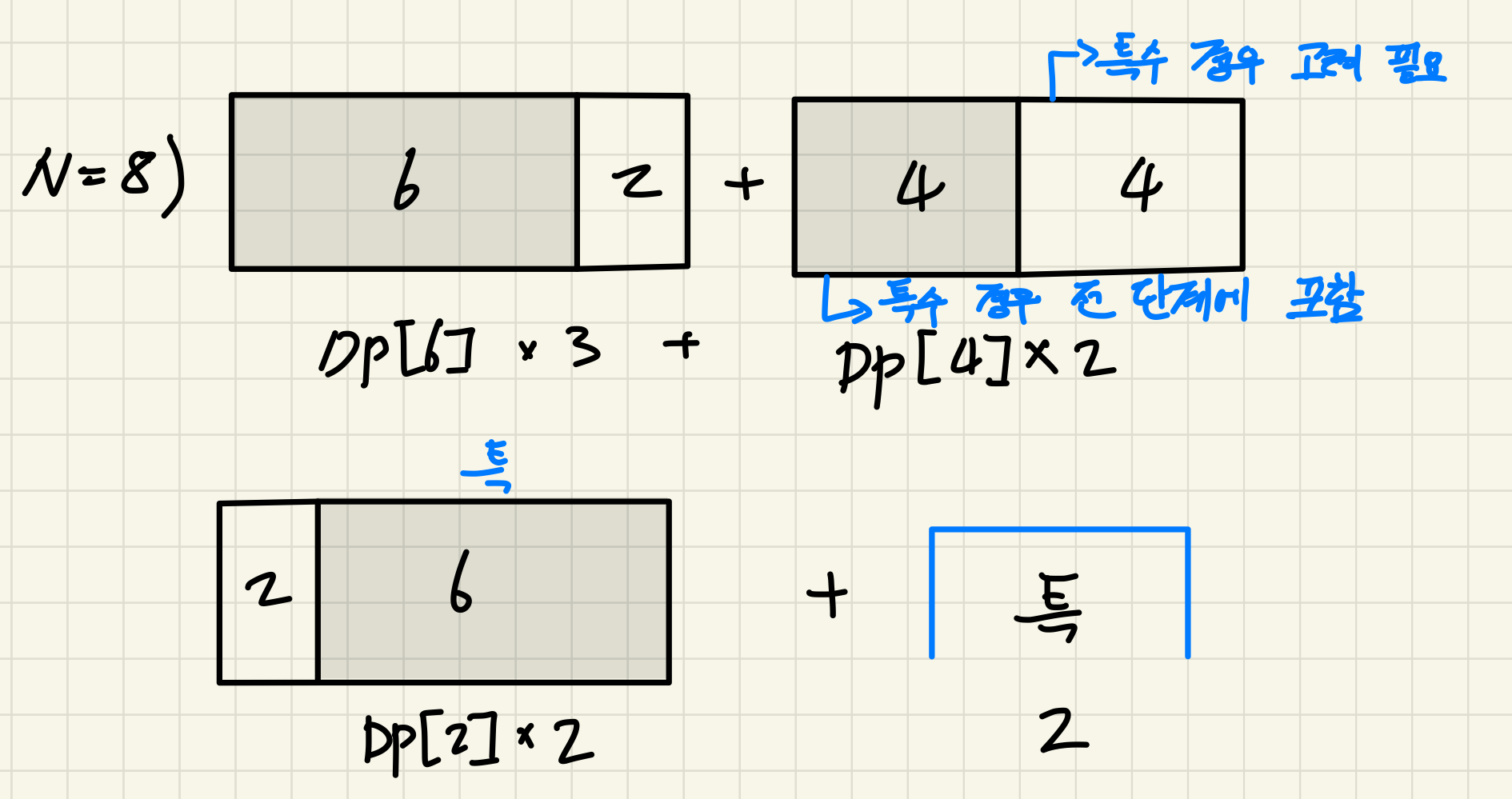
이를 점화식처럼 표현해보면,

dp[n] = 3*dp[n-2] + 2*dp[n-4] + ... + 2*dp[n-(n-2)] + 2(특수경우)

이를 고려하여 구현하였다.

sol

## method
def sol(n):
    if n%2 == 1 :
        return 0
    
    dp = [0 if i != 0 else 1 for i in range( (n//2) + 1 ) ] # 15
    
    for i in range(1,(n//2) + 1):
        if i == 1 : 
            dp[i] = 3 # 2개일 때 : 3가지
        else :
            dp[i] = 3 * dp[i-1] + 2 * (sum(dp[ : i-1 ]))

    return dp[-1]

## input
n = int(input())
## output
print(sol(n))

dp의 인덱스는 애초에 짝수만 가능하므로 2에 곱해지는 수를 인덱스로 부여했다.
N=2일 때는 index 1을, N=2일 때는 index 2로 표현했다.

마지막으로, dp[0] = 1로 두어 점화식에 통일성을 부여했다.