인공지능 데브코스 3w-1 TIL : Numpy

JeongYeon-Kim·2023년 9월 4일

데브코스

목록 보기

3/14

TIL

오늘은 기존에 배웠던 선형대수이론을 컴퓨터에서 활용할 수 있는, 파이썬 라이브러리 Numpy에 대한 수강 기록입니다.

Numpy는 행렬이나 큰 규모의 다차원 배열을 처리할 수 있게끔 지원되는 파이썬의 라이브러리입니다. 기존 파이썬의 List에서의 계산 속도를 보완하여 수치 계산을 위해 효율적으로 구현된 기능을 제공하고, 선형대수에서 활용할 수 있는 여러 행렬 연산 툴을 제공해줍니다.
또한 이후에 scipy나 pandas의 객체로도 사용되며, index slicing과 같은 다양한 코드 표현법을 인공지능에서의 pytorch와 tensorflow에 사용하는 경우가 많습니다. 따라서 numpy의 활용법에 익숙해질 필요가 있습니다.

앞으로의 내용에서 저에게도 명확한 정리가 필요했던 numpy.array()와 파이썬의list()의 차이에 대해서 살펴본 후, numpy에서의 다양한 연산을 알아보겠습니다.

🧐 numpy.array와 list

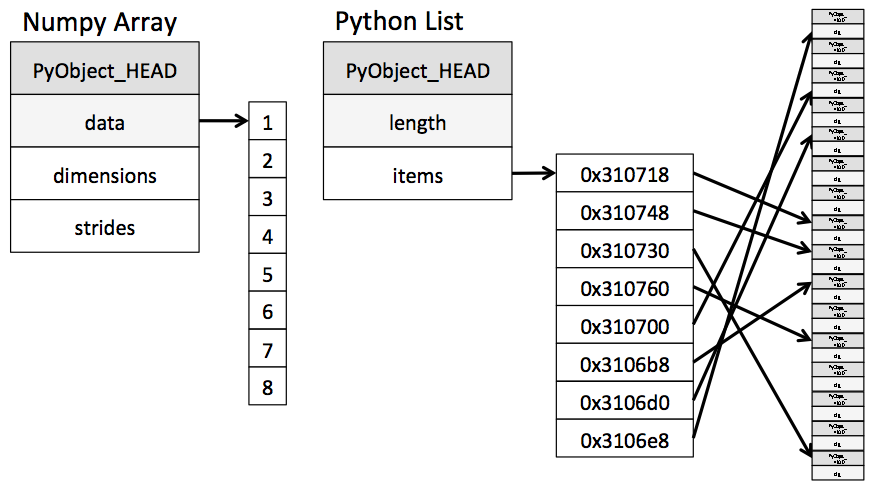
먼저는 numpy.array()와 list()의 차이부터 알아보려 합니다.

메모리 차원에서 파이썬의 list는 원소값이 아닌 원소가 저장된 주소값을 저장해놉니다. 이로서 자료형에 관계없이 값을 저장할 수 있는 다이나믹 타이핑이 가능합니다. 하지만 하나의 자료형을 저장한다고 하면 이와같이 불연속적으로 데이터를 저장하는 것은 비효율적일 수 있습니다. (굳이? 싶을 수 있겠죠)

반대로 numpy.array()는 C언어의 array와 같이 연속된 주소에 원소들을 저장합니다. 데이터에 대해 효율적으로 저장할 수 있으며, 하나의 자료형만 저장할 수 있습니다.
예시로, 만일 string과 int형 데이터가 저장된다면, 모두 string으로 간주하게 됩니다.

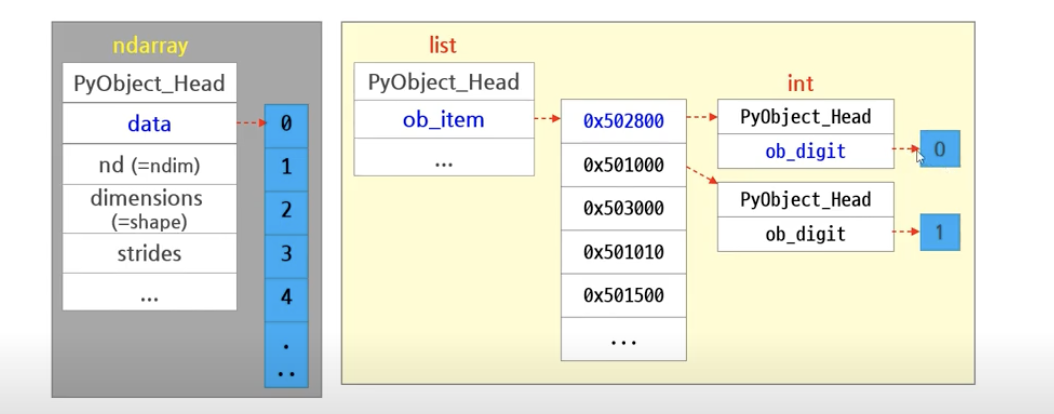
list원소들은 모두 파이썬의 '객체'로 저장이 되어 있어 주소값 접근 -> 해당 객체의 item (예시에선 ob_digit)에 접근해야합니다. 즉, 원소값에 대한 메모리 access가 여러번 발생해 속도가 느립니다. 만일 list의 차원이 증가하면 메모리 접근량이 더욱 늘어날 것입니다.

반면 numpy.array()는 연속된 주소에 저장된 해당 원소를 바로 참조할 수 있습니다.

따라서 수식 사용이나 행렬 및 다차원 배열 계산과 같은numpy가 사용되는 상황은 여러 타입의 데이터 형을 저장하는 경우도 적고 빠른 계산 처리를 원하므로, 더 빠른 numpy.array()를 사용하는 것을 알 수 있겠습니다.

🧮 Numpy 연산

지금부터는 numpy 내에서의 연산에 대해 정리해보려 합니다.
Vector와 Scalar사이에서의 연산과, 기존 list보다 더욱 편하게 접근할 수 있는 index slicing에 대한 내용을 다룰 예정입니다.

Vector : 벡터

먼저 벡터란 무엇일까요?

$\overrightarrow x = \begin{pmatrix}1\\2\\3\end{pmatrix}$

위의 예시처럼 가로나 세로로 늘여진 숫자로 이루어진 array혹은 list로 생각할 수 있겠습니다.

이를 3차원에 표기해보면 아래와 같겠습니다.

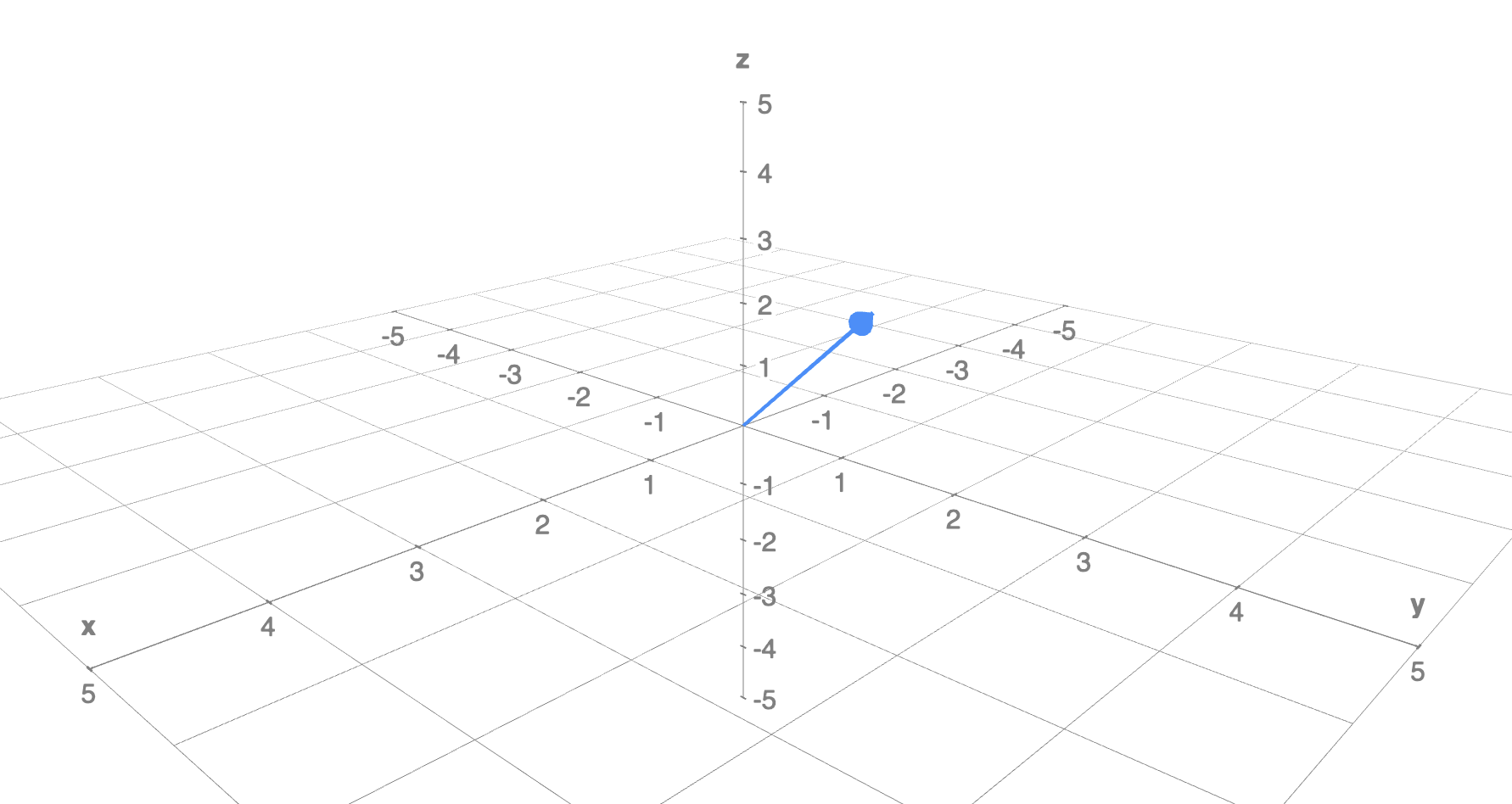
즉, 벡터는 시작점을 원점으로 고정하면 곧 해당 차원에서의 점이 된다는 것을 알 수 있습니다.

어떤 벡터 $\overrightarrow x$ 가 $n$ 개의 원소를 가진다면, 그 벡터는 $n$ 차원 벡터입니다. 벡터는 크기와 방향을 가지며 이는 원소의 숫자와 부호로 표기가 됩니다.

예시에서의 벡터는 곧 3차원 벡터이며, 3차원 내의 점임을 알 수 있었습니다.

이 때 $\overrightarrow x = \begin{pmatrix}1\\2\\3\end{pmatrix}$ 의 벡터를 열벡터, $\overrightarrow x = \begin{pmatrix}1&2&3\end{pmatrix}$ 모양의 벡터를 행벡터라고 합니다.

TMI 1

Vector는 array의 Rank가 1일 때를 말하는데요. 아래 내용을 참고로 알아두면 좋을 듯 합니다.

Rank에 따른 array의 이름

Rank Name Ex
0 Scalar(상수) 6
1 Vector $[1,2,3]$
2 matrix $[[1,2],[3,4]]$
3 3-Tensor (3차원 Tensor)
$n$ $n$ -Tensor (n차원 Tensor)

Rank	Name	Ex
0	Scalar(상수)	6
1	Vector	$[1,2,3]$
2	matrix	$[[1,2],[3,4]]$
3	3-Tensor (3차원 Tensor)
$n$	$n$ -Tensor (n차원 Tensor)

Vector와 Scalar 사이의 연산

이제 벡터와 스칼라사이 연산에 대해 다루려 합니다. 이 때는 벡터의 각 원소에 대한 연산을 진행합니다.

$x=\begin{pmatrix} 1\\2\\3\end{pmatrix}, c=5$

이 예시에 대한 결과를 코드를 통해 작성해보겠습니다.

import numpy as np

x = np.array([1,2,3])
c = 5
print(f'더하기 : {x+c}')
print(f'빼기 : {x-c}')
print(f'곱하기 : {x*c}')
print(f'나누기 : {x/c}')

더하기 : [6 7 8]
빼기 : [-4 -3 -2]
곱하기 : [ 5 10 15]
나누기 : [0.2 0.4 0.6]

이렇듯, 각 원소에 대해 스칼라만큼의 연산을 수행하는 것을 볼 수 있습니다.

Vector와 Vector사이의 연산

이번엔 벡터끼리의 연산입니다. 이 때는 벡터의 같은 index끼리 연산됩니다.

$y=\begin{pmatrix} 1\\3\\5\end{pmatrix}, z=\begin{pmatrix} 2\\9\\20\end{pmatrix}$

y = np.array([1,3,5])
z = np.array([2,9,20])

print(f'더하기 : {y+z}')
print(f'빼기 : {y-z}')
print(f'곱하기 : {y*z}')
print(f'나누기 : {y/z}')

더하기 : [ 3 12 25]
빼기 : [ -1  -6 -15]
곱하기 : [ 2 27 100]
나누기 : [0.5 0.33333333 0.25]

Indexing & slicing

이번엔 numpy에서 편리하게 수행할 수 있는 인덱스 슬라이싱입니다.

$w=\begin{pmatrix} 1&2&3&4\\5&6&7&8\\9&10&11&12\end{pmatrix}$

만약 7라는 원소를 출력하고 싶다면 W[1][2]처럼 인덱싱을 하지만, numpy에서는 W[1,2]로 적어주어도 무방합니다.

또한, 슬라이싱 할 때 파이썬 list를 사용해 $w$ 의 열벡터를 뽑아낸다고 하면 다소 여러 작업을 거쳐야 했던 반면, numpy의 array에서는 보다 쉽게 접근할 수 있습니다.

w = np.arange(1,13).reshape(3,4)

# 열벡터 확인
for c in range(4):
    print(w[:,c], end = ' ')

[ 1 5 9] [ 2 6 10] [ 3 7 11] [ 4 8 12]

Array의 Broadcasting

numpy가 연산하는 특정한 방법입니다.

Broadcasting :같은 데이터 형식의 행렬이 아니더라도 연산 가능하도록 변환하여 연산을 수행하는 것을 말합니다.

1. $M\times N$ - $M\times 1$ : 행렬과 열벡터 사이 연산

$\begin{pmatrix} 1&2&3&4\\5&6&7&8\\9&10&11&12\end{pmatrix}+\begin{pmatrix} 0\\1\\0\end{pmatrix}$

즉, 이와 같이 행렬에 열벡터를 더하는 것과 같은 연산을 말하는데, 선형대수에서는 이와같은 연산은 수행될 수 없으나 numpy array에서는 아래처럼 바꿔서 연산합니다.

$\begin{pmatrix} 1&2&3&4\\5&6&7&8\\9&10&11&12\end{pmatrix}+\begin{pmatrix} 0&0&0&0\\1&1&1&1\\0&0&0&0\end{pmatrix}$

이처럼 연산을 수행해야할 형과 크기로 바꿔서 연산해주기 때문에 Broadcasting이라는 말이 나오게 된 것입니다.

import numpy as np

a = np.arange(1,13).reshape(3,4)
x = np.array([0,1,0])
x = x[:, None] # Transpose

print(a+x)

[[ 1  2  3  4]
 [ 6  7  8  9]
 [ 9 10 11 12]]

아, 여기서 x[:, None]식은 행벡터를 열벡터로 해주기 위함인데, 이는 $x$ 가 1차원 벡터로 선언되어 x.T과 같은 Transpose관련 메소드 사용 시 만족스러운 결과가 나오지 않습니다.

x[:, None]와 같은 표현은 차원을 하나 추가해주는 것으로, 여기서는 열방향으로 차원을 추가함으로서 1차원이었던 벡터의 원소들을 열에 하나씩 추가하게 됩니다. 따라서 아래와 같이 바뀌는 것입니다.

x = np.array([0,1,0])# 행벡터:1차원 : (3, )

print(x[:,None]) # 차원 축 추가 (3,1)

<output> : shape - (3,1)
[[0]
 [1]
 [0]]

추가하고자 하는 방향으로 None을 넣어주면 됩니다. 차원 추가를 행방향으로 하면 아래처럼 됩니다.

x = np.array([0,1,0])# 행벡터:1차원
print(x[None,:]) # 차원 축 추가 : shape (1,3)

[[0 1 0]]

이번엔 행방향으로 벡터의 모든 원소가 추가된 것을 볼 수 있겠습니다.

추가로, x[:, None]를 이렇게도 사용 가능합니다!

print(x[:,np.newaxis])

2. $M\times N$ - $1\times N$ : 행렬과 행벡터 사이 연산

$\begin{pmatrix} 1&2&3&4\\5&6&7&8\\9&10&11&12\end{pmatrix}* \begin{pmatrix} 0&1&-1&-11\end{pmatrix}$

마찬가지로 broadcasting 후, 인덱스끼리의 곱셈을 진행하게 됩니다.

y = np.array([0,1,-1,-11])
print(a*y)

[[   0    2   -3  -44]
 [   0    6   -7  -88]
 [   0   10  -11 -132]]

3. $M\times 1$ - $1\times N$ : 열벡터와 행벡터 사이 연산

$\begin{pmatrix} 1&2&3\end{pmatrix}+\begin{pmatrix} 2\\0\\-2\end{pmatrix}$

이럴 때는 아래와 같이 broadcasting이 일어납니다.

$\begin{pmatrix} 1&2&3\\1&2&3\\1&2&3 \end{pmatrix}+ \begin{pmatrix} 2&2&2\\0&0&0\\-2&-2&-2\end{pmatrix}$

이렇게 되면 같은 index끼리 연산을 수행해주겠군요.

cv = np.array([1,2,3])
rv = np.array([2,0,-2])[:,None]
print(cv+rv)

[[ 3  4  5]
 [ 1  2  3]
 [-1  0  1]]

선형대수에서의 활용

이번엔 선형대수에서의 연산을 어떤 메소드로 수행하는지 주목해서 보면 도움될 듯합니다. 코드 실습과 관련된 내용이므로 주석을 덧붙여 추가하였습니다.

영행렬 : `.zeros()

# 영행렬
np.zeros((3,3))

array([[0., 0., 0.],
       [0., 0., 0.],
       [0., 0., 0.]])

(모든 원소가 1인) 행렬 : .ones()

# 모든 원소 1인 행렬
np.ones(2), np.ones((2,2))

(array([1., 1.]),

 array([[1., 1.],
        [1., 1.]]))

대각행렬 : .diag()

# 대각행렬
np.diag((1,2,3,4))

array([[1, 0, 0, 0],
       [0, 2, 0, 0],
       [0, 0, 3, 0],
       [0, 0, 0, 4]])

항등행렬 $I$ : .eye()

# 항등행렬 : I
# dtype = int, uint, float, complex,... 
np.eye(3, dtype = float).dtype

array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

행렬곱 : 내적 .dotor @

$\begin{pmatrix}1&4&3\\2&3&2\\1&2&3 \end{pmatrix} \cdot \begin{pmatrix}7&9&1\\1&6&5\\0&9&2 \end{pmatrix}$

# 행렬곱 : 내적의 결과
m1 = np.array([[1,4,3],[2,3,2],[1,2,3]])
m2 = np.array([[7,9,1],[1,6,5],[0,9,2]])

m1.dot(m2)

array([[11, 60, 27],
       [17, 54, 21],
       [ 9, 48, 17]])

이 때 .dot와@ 연산결과는 3차원 이상의 array에서는 다릅니다.

m1 @ m2

array([[11, 60, 27],
       [17, 54, 21],
       [ 9, 48, 17]])

트레이스(trace : 대각 원소의 합) .trace()

# trace
np.eye(4,dtype=float).trace()
# result : 4

행렬식 : .linalg.det()

\begin{vmatrix}1&4&3\\2&3&2\\1&2&3 \end{vmatrix}

위 행렬식이 아래 코드 m1의 행렬입니다.

# 행렬식 - linear algenbra 라이브러리
np.linalg.det(m1)

-8.000000000000002

역행렬 : .linalg.inv()

# 역행렬 - linear algenbra 라이브러리
m1_inv = np.linalg.inv(m1)
m1_inv

확인하려면 $AA^{-1}=I$ 연산을 해봅니다.

m1 @ m1_inv

array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

고유값, 고유벡터 : .linalg.eig()

# 고유값과 고유벡터
np.linalg.eig(m1)

이러면 고유값과 각 고유값에 대한 고유벡터가 출력되는 것을 볼 수 있습니다.

EigResult(eigenvalues=array([ 6.82842712, -1.        ,  1.17157288]), 
eigenvectors=array([[-6.50840283e-01, -8.94427191e-01, -2.33811454e-01],
       				[-5.89767825e-01,  4.47213595e-01, -5.89767825e-01],
       				[-4.78101286e-01,  5.26225819e-17,  7.72985198e-01]]))

이를 확인해보려면, 고유치 고유벡터의 만족하는 성질인 $ax = \lambda x$ 을 이용해 확인할 수 있습니다.

기타

▫️ `np.array_split()`

배열을 일정한 크기로 분할합니다.

예시

import numpy as np

x = np.ones((500,5000)) # 모든 원소가 1인, shape (500,5000)인 행렬

np.array_split(x, 5, axis = 0)

[array([[1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.],
        ...,
        [1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.]]),
 array([[1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.],
        ...,
        [1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.]]),
 array([[1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.],
        ...,
        [1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.]]),
 array([[1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.],
        ...,
        [1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.]]),
 array([[1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.],
        ...,
        [1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.],
        [1., 1., 1., ..., 1., 1., 1.]])]

이렇듯 n개로 분할한 array들을 list에 저장된 모습을 알 수 있습니다.

axis=0은 곧 0번째 차원축(가장 높은 차원의 축)을 기준으로 x배열에 대해5개로 분할한다는 뜻입니다.
즉 ( $500\times 5000$ ) 크기의 배열이 ( $100\times 5000$ ) 크기로 분할되는 것입니다.

np.array_split(x,5,axis=1)[0].shape

(500, 1000)

이렇듯 지정한 차원축을 n개로 분할하는 것을 볼 수 있습니다.

▫️ `np.bincount()`

해당 값의 빈도수를 해당 값이 index인 곳에 저장합니다.

np.bincount([1,2,3,2,9,9,9])

array([0, 1, 2, 1, 0, 0, 0, 0, 0, 3])

▫️ `np.argmax()` or `.argmax()`

값이 가장 큰 index를 return합니다.

np.array([1,2,3,2,9,9,9]).argmax()

▫️ `np.argsort()`

인자로 들어온 배열을 오름차순으로 정렬했을 때 순서로 원소의 원래 index를 return합니다.

import numpy as np

np.argsort([1,4,2,0,-1]

array([4, 3, 0, 2, 1])

즉, -1은 가장 작은 수로 첫 번째 위치하여 맨 처음 index에 원래 index(4번 인덱스)를 저장합니다. 마찬가지 방법으로 나머지도 진행합니다.

JeongYeon-Kim

SSU

이전 포스트

인공지능 데브코스 2w-5 TIL : 선형시스템

다음 포스트

인공지능 데브코스 3w-1 TIL : Numpy

데브코스

TIL

🧐 numpy.array와 list

🧮 Numpy 연산

Vector : 벡터

TMI 1

Vector와 Scalar 사이의 연산

Vector와 Vector사이의 연산

Indexing & slicing

Array의 Broadcasting

1. $M\times N$ - $M\times 1$ : 행렬과 열벡터 사이 연산

2. $M\times N$ - $1\times N$ : 행렬과 행벡터 사이 연산

3. $M\times 1$ - $1\times N$ : 열벡터와 행벡터 사이 연산

선형대수에서의 활용

기타

▫️ `np.array_split()`

▫️ `np.bincount()`

▫️ `np.argmax()` or `.argmax()`

▫️ `np.argsort()`

인공지능 데브코스 2w-5 TIL : 선형시스템

인공지능 데브코스 3w-2 TIL : Numpy - dot()과 matmul()의 차이, broadcasting, Bool indexing과 Fancy indexing

0개의 댓글

인공지능 데브코스 3w-1 TIL : Numpy

데브코스

TIL

🧐 numpy.array와 list

🧮 Numpy 연산

Vector : 벡터

TMI 1

Vector와 Scalar 사이의 연산

Vector와 Vector사이의 연산

Indexing & slicing

Array의 Broadcasting

1. M×NM\times NM×N - M×1M\times 1M×1 : 행렬과 열벡터 사이 연산

2. M×NM\times NM×N - 1×N1\times N1×N : 행렬과 행벡터 사이 연산

3.M×1M\times 1M×1 - 1×N1\times N1×N : 열벡터와 행벡터 사이 연산

선형대수에서의 활용

기타

▫️ np.array_split()

▫️ np.bincount()

▫️ np.argmax() or .argmax()

▫️ np.argsort()

인공지능 데브코스 2w-5 TIL : 선형시스템

인공지능 데브코스 3w-2 TIL : Numpy - dot()과 matmul()의 차이, broadcasting, Bool indexing과 Fancy indexing

0개의 댓글

1. $M\times N$ - $M\times 1$ : 행렬과 열벡터 사이 연산

2. $M\times N$ - $1\times N$ : 행렬과 행벡터 사이 연산

3. $M\times 1$ - $1\times N$ : 열벡터와 행벡터 사이 연산

▫️ `np.array_split()`

▫️ `np.bincount()`

▫️ `np.argmax()` or `.argmax()`

▫️ `np.argsort()`