TIL

선형 시스템이란?

오늘의 학습내용은 선형 시스템에 관련된 내용입니다.
선형 시스템이란, 흔히 생각하는 연립방정식에서 행렬끼리의 곱 형태로 나타낸 방식입니다. 아래 식을 참고해보겠습니다.

$\begin{cases}3x + y -z = 4\\x - 2y -z = 1\\x + y + z = 2\end{cases} \to \begin{pmatrix}3&1&-1 \\1&-2&-1 \\ 1&1&1 \end{pmatrix} \begin{pmatrix}x \\y \\ z \end{pmatrix} = \begin{pmatrix} 4 \\1 \\2 \end{pmatrix}$

이처럼 미지수 앞의 계수들을 따로 행렬의 형태로 빼내어 나타낼 수 있게됩니다.
이때 좌측 연립방정식의 모양을 선형 방정식, 우측 행렬의 곱 형태로 나타낸 것이 선형 시스템입니다.

오늘은 이처럼 $Ax=b$ 형태의 선형시스템에 대해 다양한 접근을 해보고, 그에 따른 해석을 어떻게 할 수 있는지 정리해보려고 합니다.

먼저는 이렇게 생긴 선형시스템의 해는 어떻게 구하는지 살펴보고, 이를 선형 결합과 선형 변환에서 어떻게 접근하는지 살펴보겟습니다.

선형시스템의 해

$m\times n$행렬 $A$에 대한 선형시스템 $Ax = b$에서의 특징이 다음과 같이 나타난다는 것을 알 수 있습니다.

• $m$은 선형방정식의 개수
• $n$은 미지수의 개수
• A는 $m\times n$행렬
• $x$는 $n$차원 벡터
• $b$는 $m$차원 벡터

선형시스템 $Ax=b$가 가질 수 있는 해의 경우의 수는 세가지가 됩니다.

1. 해가 하나인 경우 consistent
2. 해가 없는 경우 inconsistent
3. 해가 여러개인 경우 consistent

이 때, 선형시스템이 consistent하다는 것은 선형시스템의 해가 존재하며, inconsistent하다는 것은 해가 존재하지 않는다는 것을 말합니다.

여기서 A의 행렬식이 0인 경우 A를singular(특이)하다라고 표현합니다.
행렬식이 0이라는 것은 A의 역행렬이 존재하지 않으며, A가 종속이며, rank = n ($\because A$는 $m\times n$행렬)이라는 말과도 같게 되겠습니다.

그럼 각각의 경우에서 그래프상 어떻게 나타나는지 살펴보겠습니다

해가 하나있는 경우

$\begin{cases} 3x + y = 4 \\ x+2y = 3 \end{cases}$ 를 예시로 보겠습니다.

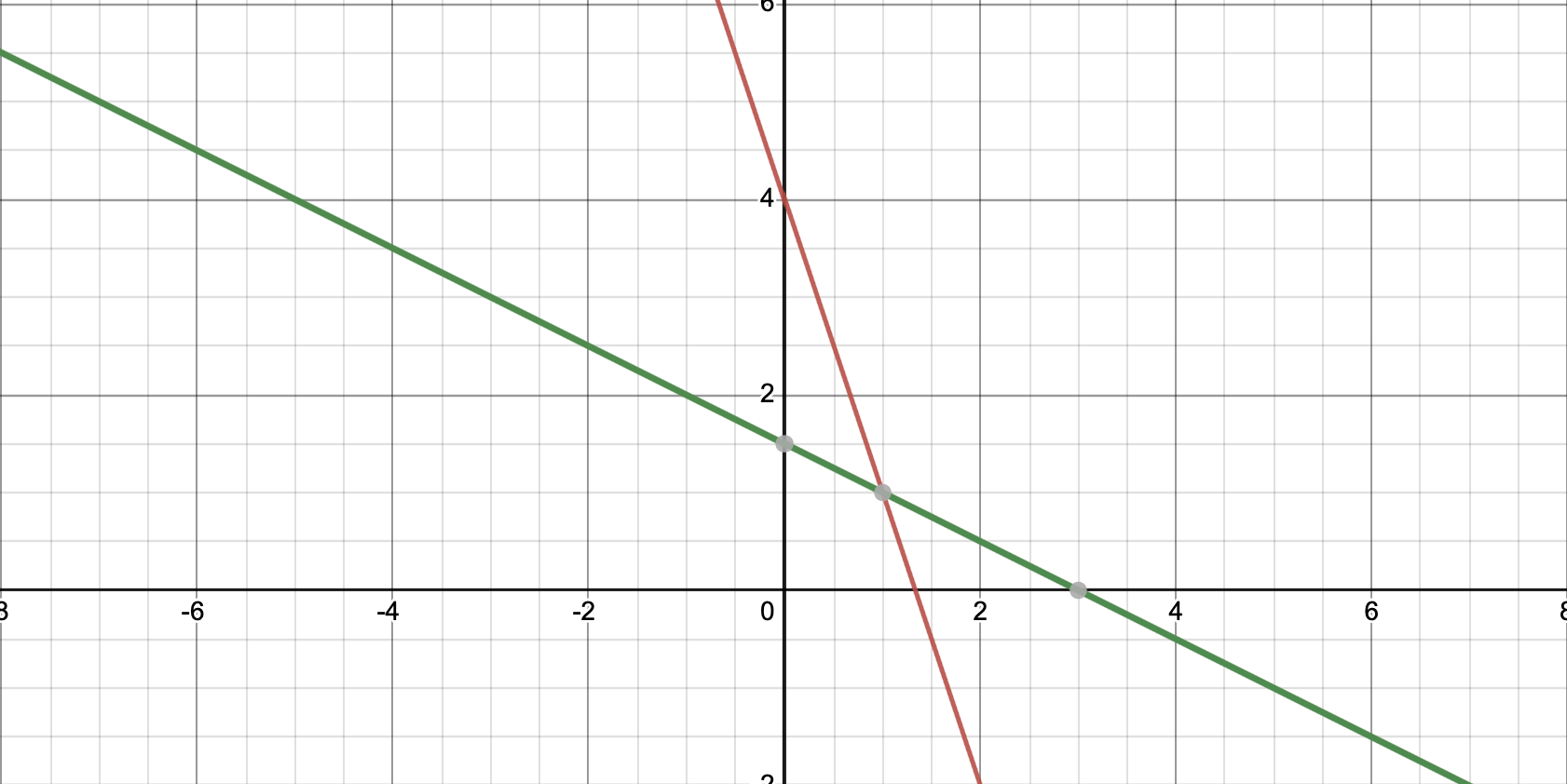
이 떄 평면상의 직선을 선형시스템으로 나타내면 다음과 같은데요.

$\begin{cases} 3x + y = 4 \\ x+2y = 3 \end{cases} \to \begin{pmatrix} 3&1 \\ 1&2\end{pmatrix}\begin{pmatrix} x \\ y\end{pmatrix} =\begin{pmatrix} 4 \\ 3\end{pmatrix}$

이 때 행렬 $\begin{pmatrix} 3&1 \\ 1&2\end{pmatrix}$에 잠시 뒤 다루게 될 가우스소거법을 적용하면 $\begin{pmatrix} 0&-5 \\ 1&2\end{pmatrix}$가 됩니다. 이 때 각 행의 모든 행원소가 0인 행이 없는 것을 볼 수 있습니다. 이때 이 행렬의 Rank는 2며, 독립임을 알 수 있게됩니다. 그 모습으로 위 그림처럼 서로 크로스하는 형태의 직선을 그리게되며, 그렇기 때문에 하나의 해를 가지는 것을 알 수 있습니다.

해가 무수히 많거나 존재하지 않는 경우

그렇다면 이 행렬의 행원소끼리 종속인 상태는 어떤 상태일까요?
예시로 아래 선형방정식을 참고하겟습니다.

$\begin{cases} 3x + y = 4 \\ 6x+2y = 3 \end{cases}$

그리고 이를 2차원 평면상에 그려보면 아래와 같습니다.

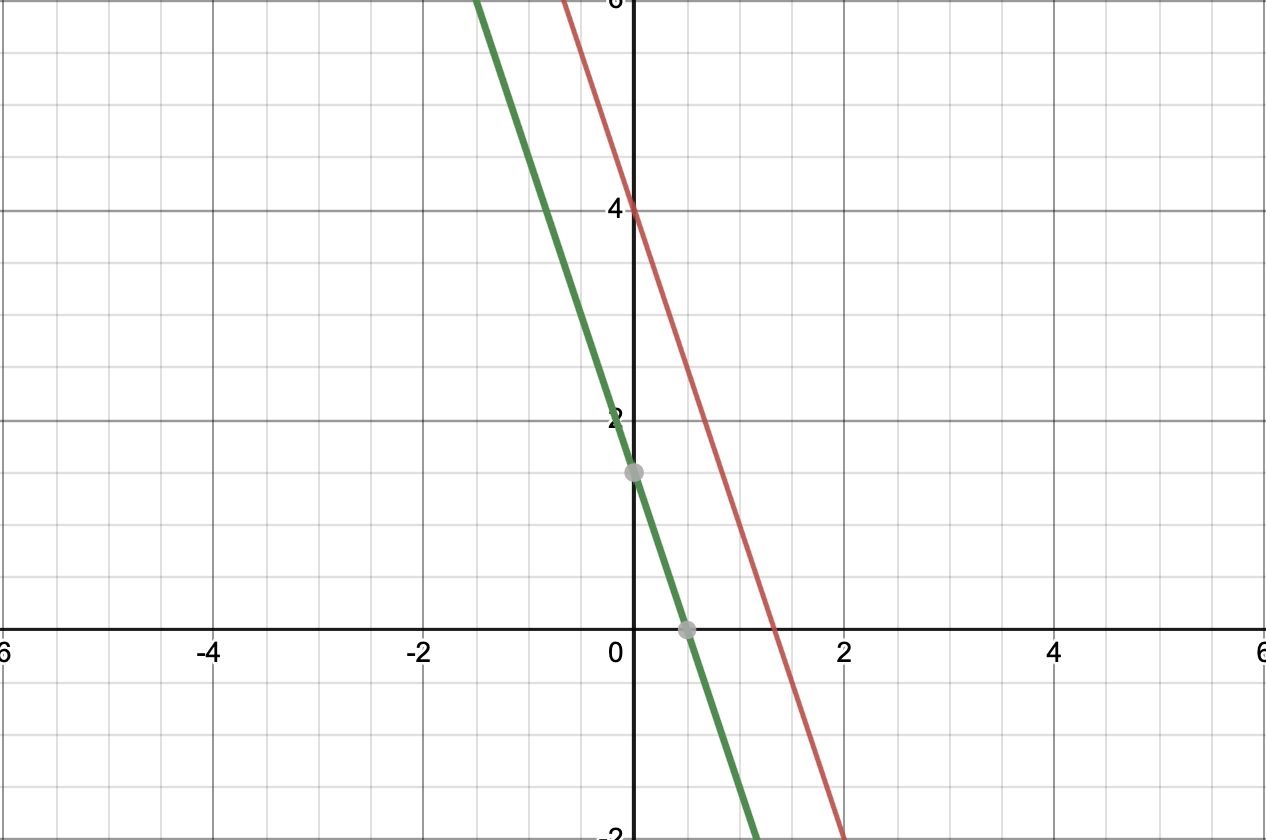
마찬가지로 선형시스템으로 나타내면

$\begin{cases} 3x + y = 4 \\ 6x+2y = 3 \end{cases} \to \begin{pmatrix} 3&1 \\ 6&2\end{pmatrix}\begin{pmatrix} x \\ y\end{pmatrix} =\begin{pmatrix} 4 \\ 3\end{pmatrix}$

이 때 $\begin{pmatrix} 3&1 \\ 6&2\end{pmatrix}$에 가우스 소거법을 적용한 결과 $\begin{pmatrix} 3&1 \\ 0&0\end{pmatrix}$을 알게됩니다. 이 때는 행원소가 모두 0인 행이 존재하므로 선형방정식이 종속관계에 있다는 것을 알 수 있는 것입니다.
이 때의 rank는 1로 행렬의 차원, 즉 행렬의 열의 개수보다 적다는 것을 알 수 있습니다.

다시말하면, 결국엔 다른 직선이 아닌 한 직선을 평행이동한 것 뿐이었다는 것이죠.
아예 겹치거나, 아예 안 만나는 경우이기에 해가 무수히 많거나, 존재하지 않는 것이었습니다.

해서 행렬 $A$가 독립일 때와 종속일 때 어떻게 해를 가지는지 알 수 있었습니다.

가우스 전방 소거법

선형 시스템 $Ax=b$의 해를 구할 때 다양한 방법으로 구할 수 있습니다.

1. $A$에 대한 가우스 전방 소거법
2. $x = A^{-1}b$ 형태와 같은 $A$의 역행렬 활용
3. LU분해

이 중에서 먼저 가우스 전방 소거법에 대해 알아보겠습니다.

가우스 소거법을 활용하면 선형시스템을 아래로 갈수록 더 간단한 형태로 정리해나갈 수 있습니다. 다시말해 A를 상삼각행렬로 만드는 행연산을 수행하는 과정이 되겠습니다.

아래의 예시처럼 기존의 행렬을 우측과 같은 상삼각행렬의 형태로 만들 수 있게됩니다.

• $\begin{pmatrix}3&1&-1 \\1&-2&-1 \\ 1&1&1 \end{pmatrix} \begin{pmatrix}x \\y \\ z \end{pmatrix} = \begin{pmatrix} 4 \\1 \\2 \end{pmatrix} \to \begin{pmatrix}a_1&a_2&a_3 \\0&a_4&a_5 \\ 0&0&a_6 \end{pmatrix} \begin{pmatrix}x \\y \\ z \end{pmatrix} = \begin{pmatrix} b_1 \\b_2 \\b_3 \end{pmatrix}$
  이렇게 나온 상삼각 행렬에서는 해를 쉽게 구할 수 있게 됩니다.
• $\begin{pmatrix}a_1&a_2&a_3 \\0&a_4&a_5 \\ 0&0&a_6 \end{pmatrix} \begin{pmatrix}x \\y \\ z \end{pmatrix} = \begin{pmatrix} b_1 \\b_2 \\b_3 \end{pmatrix}$ 형태에서 $z \to x$방향으로 해를 구해나갑니다.

이때 다음과 같은 연산을 취해 행연산을 하게 됩니다.

• 치환 : i번째 행을 m배하여 j행에 더합니다.

  $r_j \larr r_j + m\times r_i$

• 교환 : i행과 j행을 바꿉니다.

  $r_j \leftrightarrow r_j$

• 스케일링 : 해당 행을 k배(k≠0)

  $k\times r_j \to r_j$

이와 같이 행연산을 하여 행렬을 바꿔주게되면, 선형시스템의 Rank를 알 수 있게 됩니다. Rank란 행렬 내 독립인 행의 개수(행 기준)를 말합니다.

이 Rank값을 알면 앞서 언급된 것처럼 선형시스템이 어떠한 해를 가지는지 알 수 있는데요.
선형시스템이 행렬의 열 개수, 즉 행렬의 차원과 같다면 행렬이 독립이라는 얘기기 때문에 하나의 해를 갖게됩니다.

반대로 Rank값이 행렬의 열 개수보다 적다면, 종속인 행이 존재하므로 해가 존재하지 않거나 무수히 많은 해를 가지게 됩니다.

---

이처럼 전방소거법을 활용하면 선형시스템을 해를 구하기 쉬운 형태
로 바꿀 수 있음과 동시에 Rank를 알 수 있으므로 선형시스템의 consistent / inconsistent 여부를 알 수 있게 되는 것입니다.

역행렬 구하기

이번엔 역행렬을 구하여 $x = A^{-1}b$형태로 만들어 해를 구하는 방법입니다.

역행렬을 구하는 방법은 생략하고 대신 코드로 구하는 방법을 기록하도록 하겠습니다.역행렬은 numpy의 .linalg.inv()함수를 사용하면 됩니다.

import numpy as np
A_inv = np.linalg.inv(A)

print(A_inv)
print(np.shape(A_inv))

<output>

[[-0.5  1.   1.5]
 [-1.   1.   2. ]
 [ 1.5 -2.  -2.5]]
(3, 3)

LU분해

LU분해는 행렬분해를 하는 연산으로, 마치 인수분해를 해서 인수의 곱으로 나타냈던 것처럼 한 행렬을 행렬의 곱으로 나타낸 것을 말합니다.

선형결합 : Linear Comination

선형변환 : Linear Transformation