- 문제 설명
정우는 예술적 감각이 뛰어난 타일공입니다. 그는 단순한 타일을 활용하여 불규칙하면서도 화려하게 타일링을 하곤 합니다.
어느 날 정우는 가로 길이 n, 세로 길이 3 인 판을 타일링하는 의뢰를 맡았습니다. 아방가르드한 디자인 영감이 떠오른 정우는 다음과 같은 두 가지 종류의 타일로 타일링을 하기로 결정했습니다.
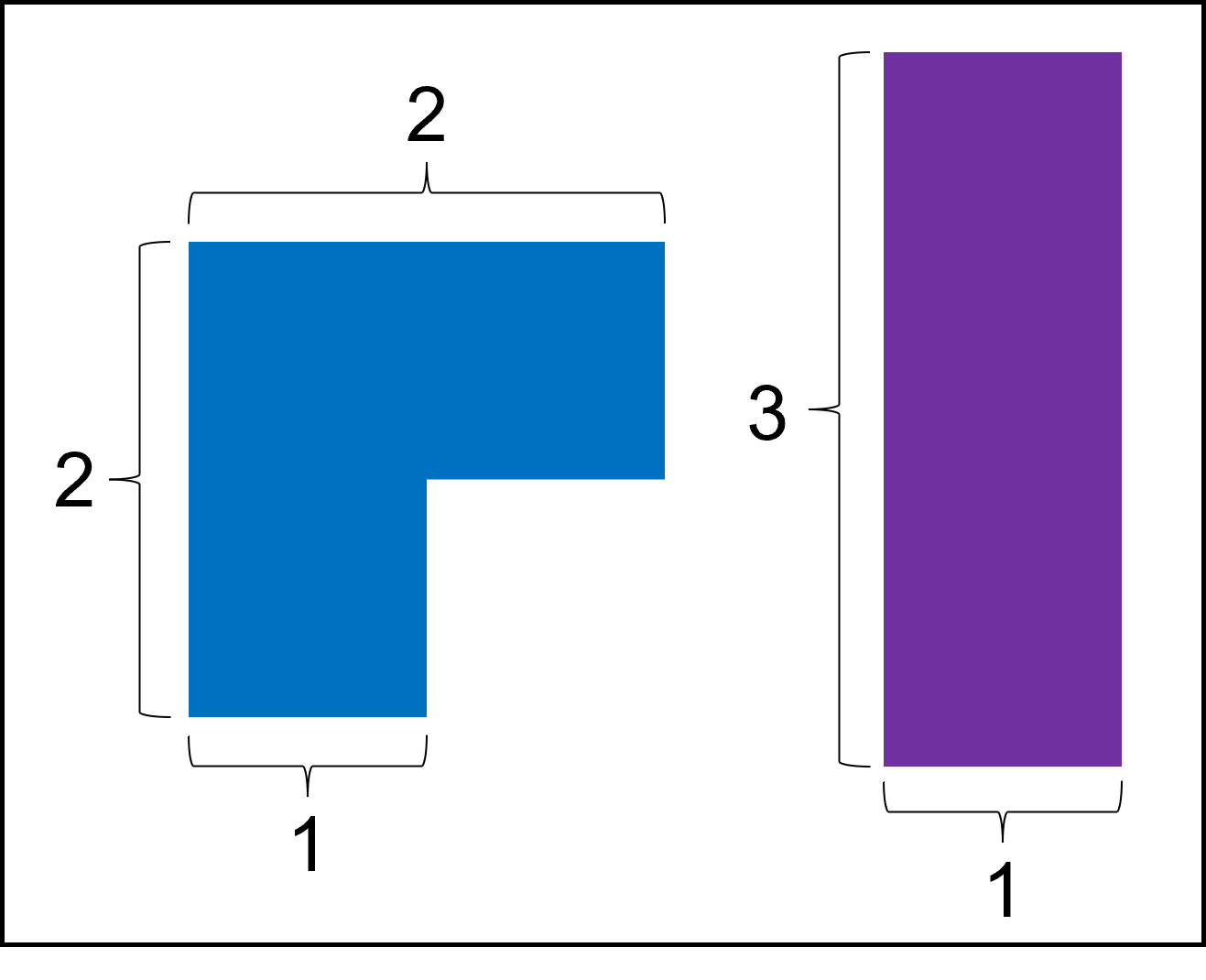
각 타일은 90도씩 회전할 수 있으며 타일의 개수는 제한이 없습니다.
n이 주어졌을 때, 이 두 가지 종류의 타일로 n x 3 크기의 판을 타일링하는 방법의 수를 return 하도록 solution 함수를 완성해주세요.
- 제한 사항
1 ≤ n ≤ 100,000
결과는 매우 클 수 있으므로 1,000,000,007 로 나눈 나머지를 return합니다.
풀이
이번엔 프로그래머스의 타일링 문제입니다.
기존 2xN,3xN 문제 유형에서 확장, 변형된 느낌의 어려운 문제였습니다.
처음 저도 생각을 많이 하고 다른 분의 풀이도 참고해보며 이해한 바를 작성한 것이라, 어느 정도 이해되신 분이면 구구절절할 수 있을겁니다. 중간 중간 스킵하여 필요한 정보 가져가시기 바랍니다 :)
문제 해결을 위해선 아래 사항을 고려해보면 좋을 것 같습니다.
- 규칙 찾기
N = k일 때, k일 때의 특수한 경우를 중점으로 규칙을 찾아보았습니다.- 점화식 생성
여기까지 풀어보신 분이라면 그저 단순하게 dp방식을 이용해 구현을 했을 때 시간복잡도 때문에 시간초과를 경험해 보셨을 겁니다. 경우 별로 존재하는 규칙이 존재했었고, 이를 이용해 구현하여 이 문제를 극복할 수 있었습니다.
전반적인 얘기는 이제 접어두고, 본격적으로 파훼법을 알아보겠습니다!
규칙
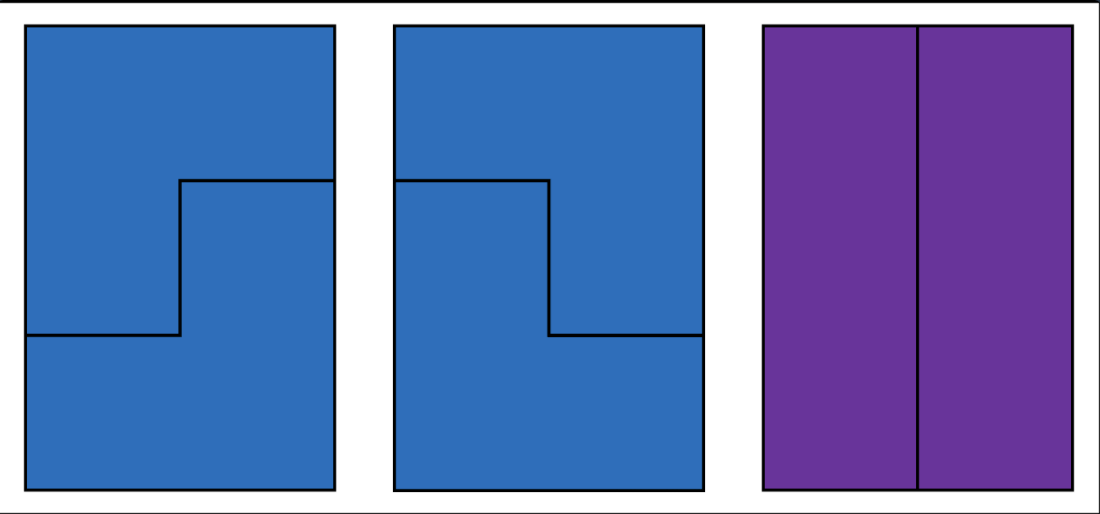
문제에서 n= 2,3일 때를 제시하여 보여주었기에 아래와 같은 경우가 나온다는 것을 알 수 있습니다.
- N = 2
- N = 3
여기서 우선 각각 경우에서 이전의 경우에서 표현하지 못하는 특수 경우를 고려하여 생각해보았습니다.
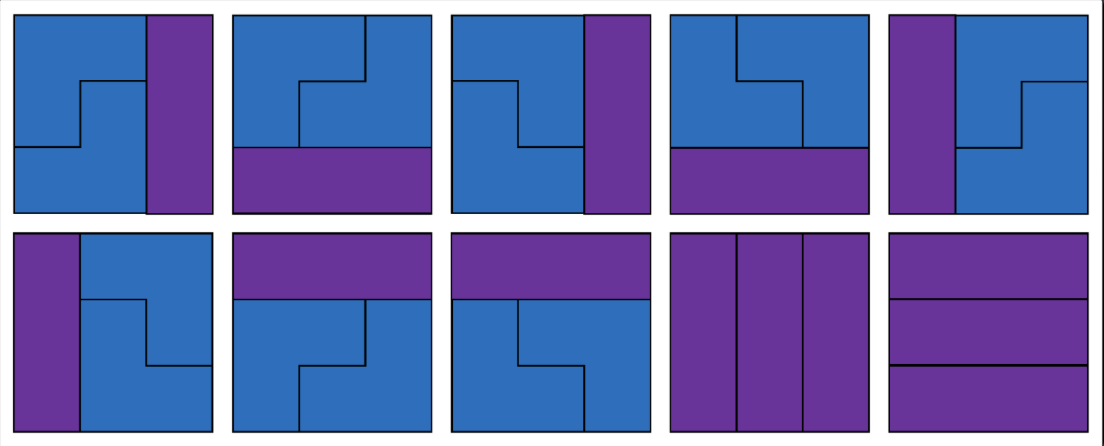
먼저 n=2일 때 가장 오른쪽의 3x1블록 두개가 서있는 모습은 n=1일때의 경우로 포함된 것이죠? 따라서 n=2에서만 나타는 특수한 경우의 수는 2가지입니다.
n=3일 때는 n=2에서의 블록이 누워있는 경우가 n=3만의 특수한 경우가 될 것입니다. 따라서 n=3에서는 5가지가 됩니다.
이것들은 다음 경우의 수를 고려할 때 이용해보겠습니다.
- N = 4
다른 경우도 마찬가지이겠지만, 4일 때 역시 이전의 경우들로 표현이 가능합니다.
그래서 이전의 경우의 수들이 어떻게 들어가는지를 기준으로 생각을 해볼겁니다!
아래처럼 우측 사각형을 기준을 잡고 하나씩 고려해볼겁니다.
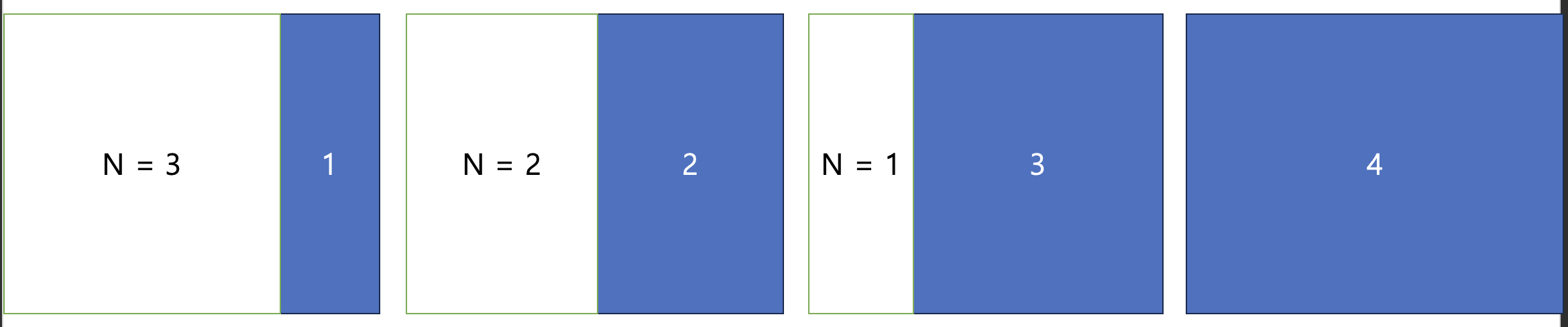
좌측 사각형 N=1일 때는 N=3인 경우와 결합이 되어있는 경우입니다. 편의상 3+1으로 고려해봤다고 해보겠습니다. 그럼 경우의 수는 dp[3]*dp[1]이겠네요.
이제 좌측 사각형이 N=2일 때를 생각해볼건데요( 2+2의 경우입니다! ), 이 때 검토해볼 것은 방금 전에 고려해봤던 3+1의 경우에서 2+2로 넘어갈 때 중복되어 고려된 경우의 수는 없는지 생각해보려 합니다!
중복상황 고려
2+2일 때, 마찬가지로 dp[2]*dp[2]로 계산하는 것이 어떤 의미인지 살펴보겠습니다.
dp[2]*dp[2]로 계산하면 아래처럼 2+( 1+1 )의 경우가 포함이 되죠. 하지만 이 경우는 3+1때 이미 고려가 된 경우죠? 따라서 방금 먼저 생각해봤던 N=2일 때의 특수한 경우만 생각해보는 겁니다.
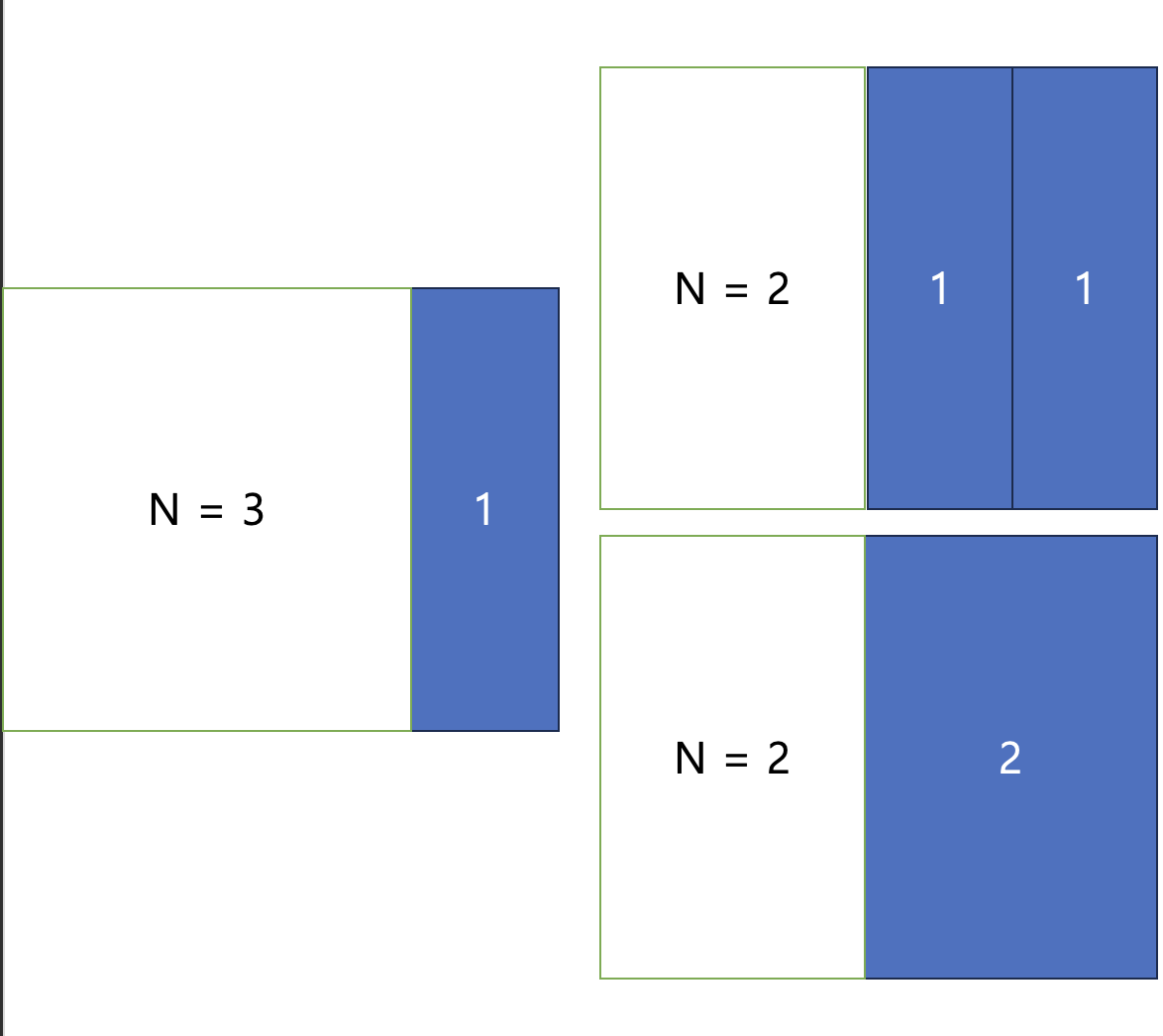이렇게 되면 이전 단계에 나왔던 경우를 제외하고 고려해볼 수 있게 되겠죠?
따라서 2+2의 경우는 dp[2]*2가 될 것입니다.
1+3일 때는 어떨까요?
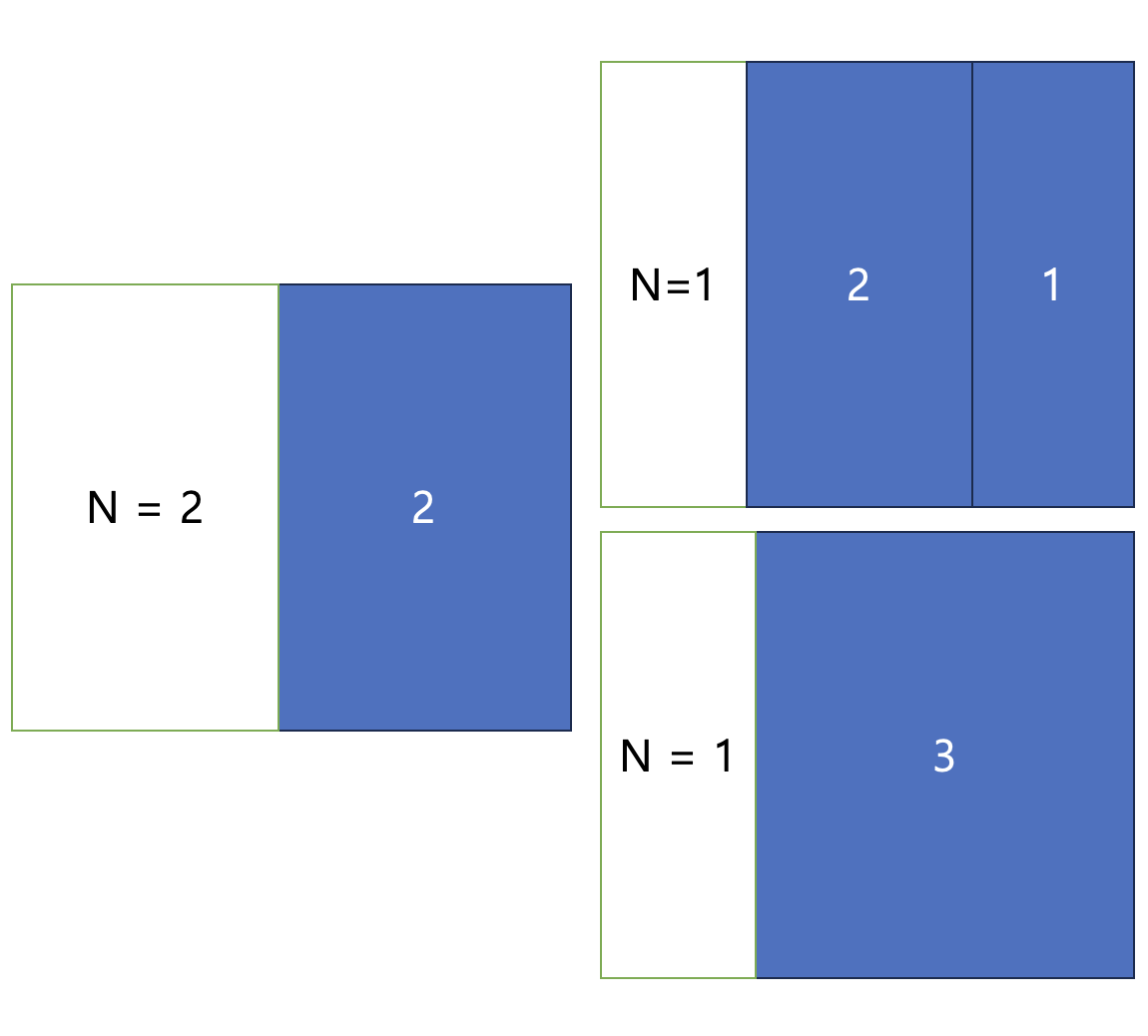1+3에서는 1+(1+2)와 1+(2+1)은 이미 앞서 고려가 되어있기 때문에 세면 안됩니다. 따라서 n=3일때의 특수한 경우만 올 수 있다고 생각할 수 있겠네요.
즉, dp[1]*5가 될 것입니다.
특수 경우 고려
그럼 N=4일 때 특수한 경우는 없는걸까요?
저도 혹시나 해서 생각을 해봤는데 존재했습니다.
풀 때 자칫 여기서 빼뜨릴 뻔 했어요 ㅎㅎ;
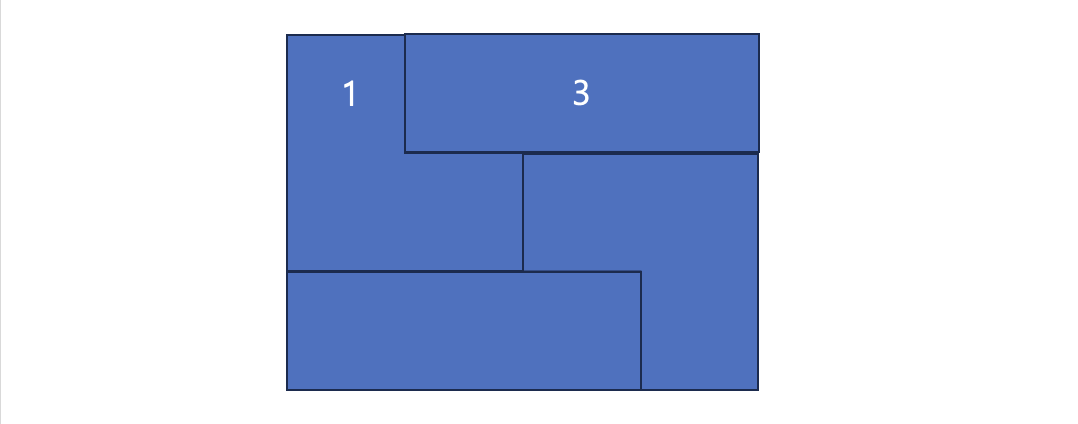위에 숫자를 표기해놓은 건, 윗 칸만을 고려했을 때 1+3칸씩 채우는 걸로 생각해볼 수 있어서 입니다. 그렇다는건 3+1경우도 존재하니 4일 떄 특수한 경우가 2가지임을 알 수 있겠군요.
이 것을 3칸씩 채우고 남은 칸을 채운다고 생각해보면 1+3+3과 같은 방식도 가능할까요?
- N%3 == 1 일 때
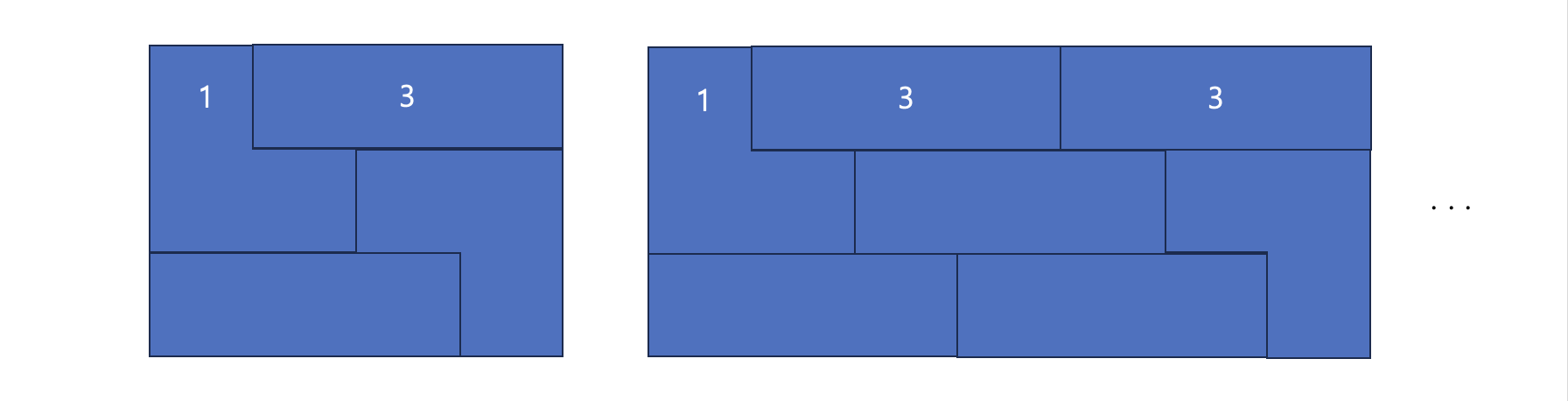네 가능합니다. 저건 N=7일 때 특수한 경우가 되겠군요.
마찬가지로 N이 계속 증가함에 따라 나타나는 특수한 경우를 생각해보면 아래와 같습니다.
- N%3 == 2 일 때
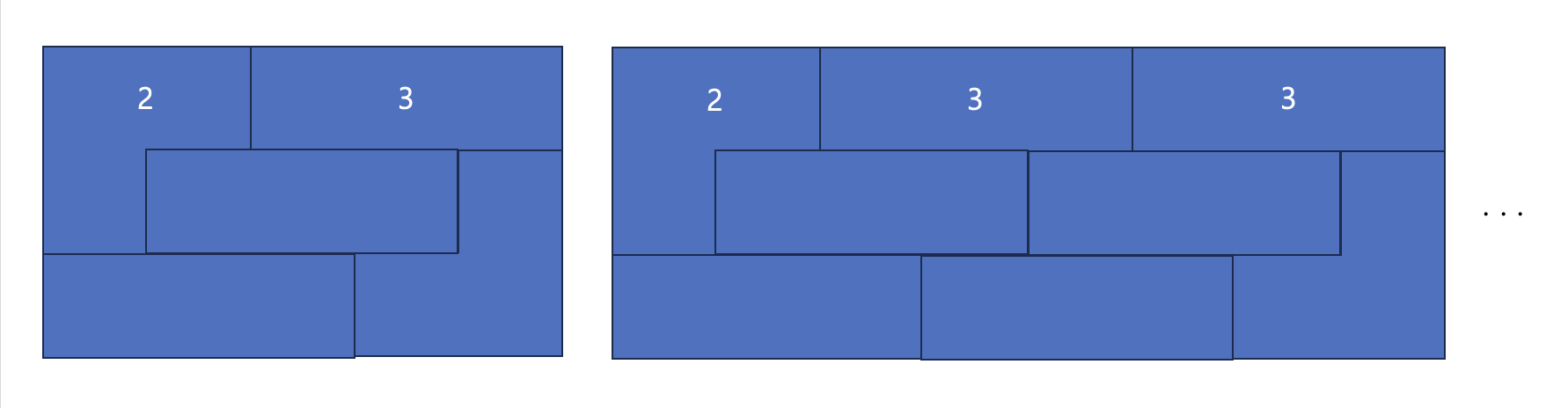좌우로 자리 바꾼다고 생각하면 이 때도 특수한 경우가 2가지네요.
- N%3 == 0 일 때
즉, 모두 세칸으로 채울 수 있다면 아래와 같겠습니다. N=6일 때 입니다.
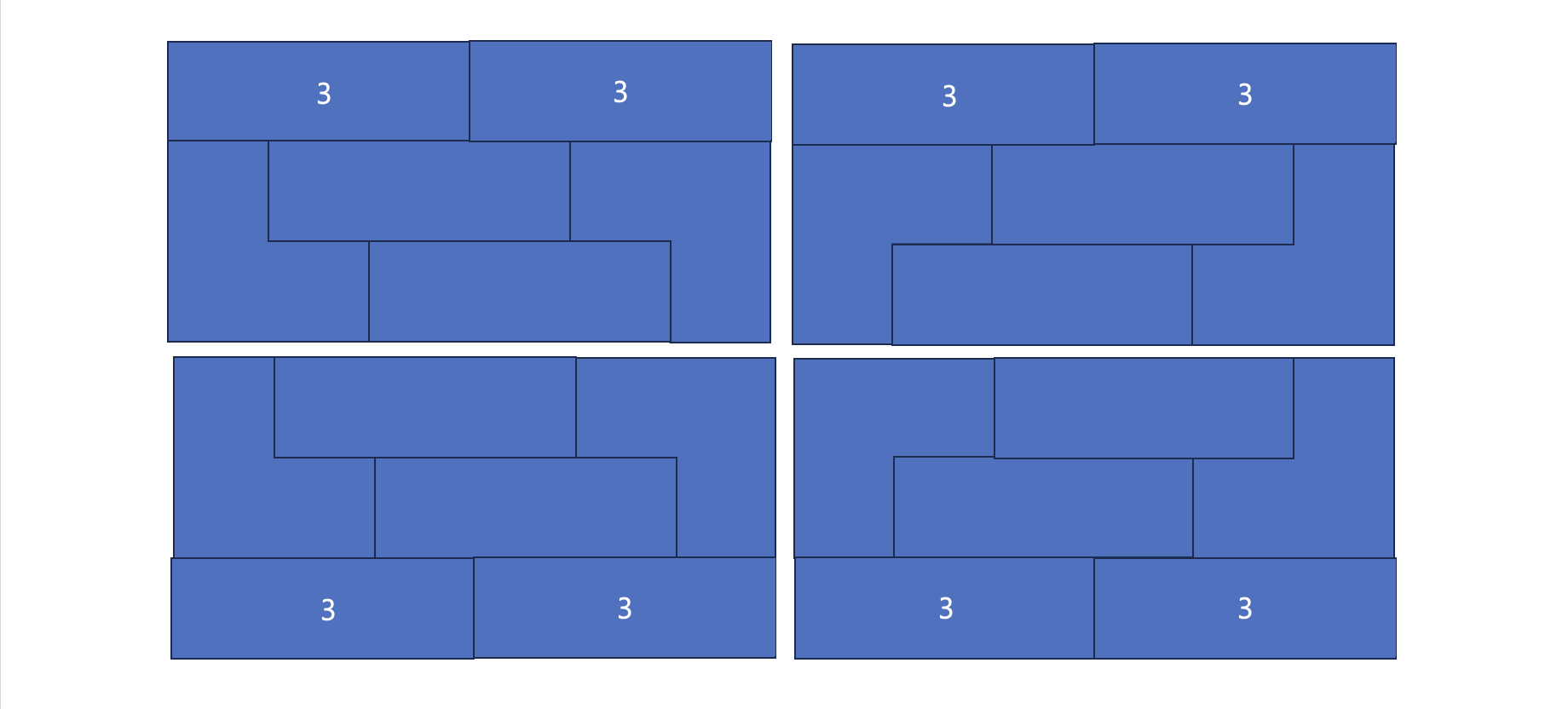k가 같은 조건일 때 마찬가지의 형태를 띄겠고, 이 조건에서는 특수한 경우가 4가지 입니다.
점화식
에로사항
발견한 규칙대로면 아래의 형태처럼 경우의 수가 나오겠네요. 간략하게 표현할게요.
dp[n] = dp[n-1]*1 + dp[n-2]*2+ dp[n-3]*3 + dp[n-4]*특 + ... + dp[1]*특 + 특개략적으로 보니, n번째 값을 찾기 위해 1 ~ (n-1)까지 참고해야 하네요.. 이러면 O(n^2)으로 시간복잡도가 높아서 시간초과가 뜰겁니다..!
sol
아까 규칙찾을 때 3으로 나눈 나머지 별로 특수한 경우가 같게 나왔던 것처럼 점화식에서도 규칙이 있을 수 있지 않을까 생각하게 되었어요. 아래처럼요!
# n%3 == 1일 때
dp[4] = dp[3]*1 + dp[2]*2 + dp[1]*5 + 2
dp[7] = dp[6]*1 + dp[5]*2 + dp[4]*5 + dp[3]*2 + dp[2]*2 + dp[1]*4 +2예시로 이 두 경우만을 가져왔습니다.
물론 이걸 풀 때 저도 저 두개만 보고 바로 캐치했던건 아니고 여러 경우들을 저런 식으로 비교 해봤던거라, 의문이 가시질 않는다면 추가로 더 해보시기 바랍니다.
자세히보면, N=7일 때 3개 항 이후에 나오는 식들은 N=4일 때 나왔던 내용입니다.
더 정확히 말하면, N=4일 때 나오는 3개항에 각각 특수경우 대신 2,2,4를 곱해서 들어가게 되네요.
나머지 2일 경우도 볼까요?
# n%3 == 2일 때
dp[5] = dp[4]*1 + dp[3]*2 + dp[2]*5 + dp[1]*2 + 2
dp[8] = dp[7]*1 + dp[6]*2 + dp[5]*5 + dp[4]*2 + dp[3]*2 + dp[2]*4 + dp[1]*2 + 2이 때도 N=5일 때의 dp[4], dp[3], dp[2]에 각각 2,2,4만 곱해져서 N=8일 때 다시 반복되는 것을 볼 수 있습니다.
이런 식이면 N%3 ==2 때 경우의 수 계산이 끝났다고 넘어가는 것이 아니라, 앞에 세 항에 2,2,4를 곱해서 더해 따로 저장해주고, 이후 N%3 ==2 인 경우일 때 불러와서 연산해주면 연산의 중복을 줄일 수 있겠습니다.
코드
def solution(n):
dp = [1,1,3,10] + [0]*(n-3)
sp_c2, sp_c3 = 2, 5
sp_cases = [12, 2, 4] #각각 6, 4, 5 일 때 초기에 더해지는 값들
if n <= 3 : return dp[n]
for idx in range(4,n+1):
sp_c = idx%3
total = sp_cases[sp_c]
total += dp[idx-1] + sp_c2*dp[idx-2] + sp_c3*dp[idx-3]
dp[idx] = total
sp_cases[sp_c] += dp[idx-1]*2 + dp[idx-2]*2 + dp[idx-3]*4
answer = dp[n]%1000000007
return answer