
LCS하면 보통 최장 공통 부분수열을 말하지만, 최장 공통 문자열을 말하기도 한다.
-
Longest Common Substring (최장 공통 문자열)
: 한번에 이어져 있어야 함
ex) ABCDEF 와 GBCDFE 의 최장 공통 문자열 = BCD -
Longest Common Subsequence (최장 공통 부분수열)
: 문자 사이를 건너뛸 수 있음
ex) ABCDEF 와 GBCDFE 의 최장 공통 문자열 = BCDF / BCDE
LCS 구현은 DP로 이루어진다. (또 DPㅡㅡ)
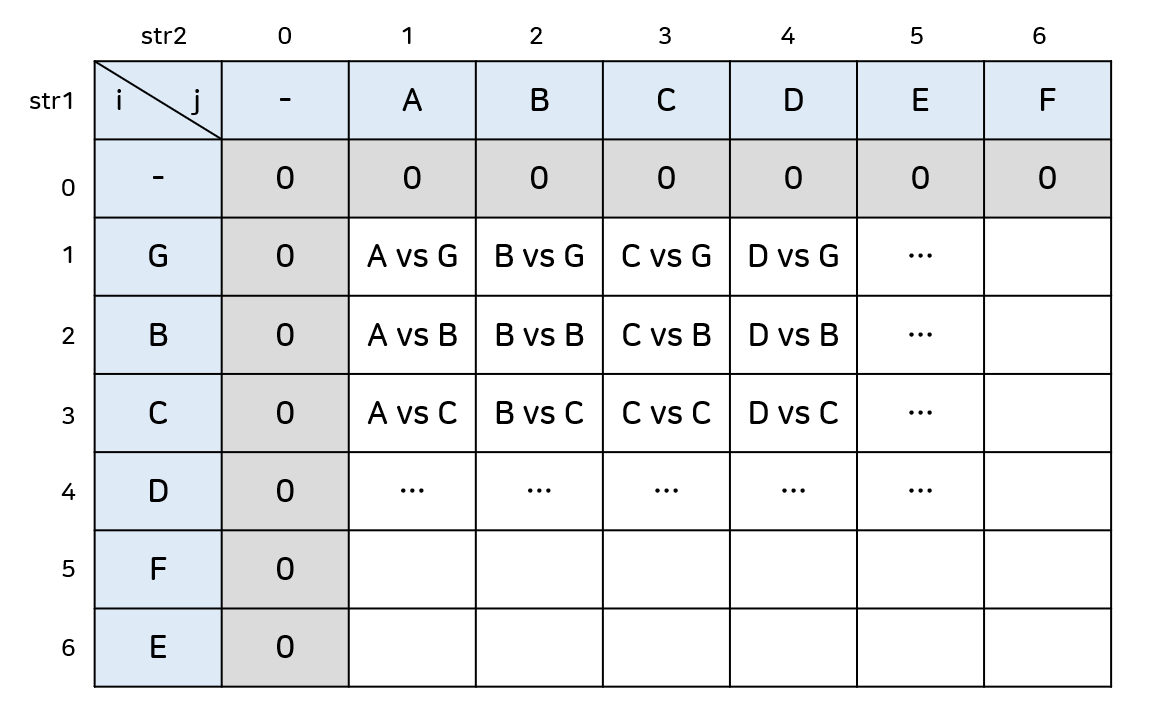
기본틀은 이렇게 문자열의 문자를 하나씩 비교해서 두 문자가 같은지, 다른지에 따라 값을 갱신한다. (이후 설명에서 아래 2차원배열을 LCS라 부른다.)
1. 최장 공통 문자열
(1) LCS에는 무슨 값이 들어가는가?
LCS가 정확히 뭘 담는건지 모르겠어서 고민을 많이 했는데, 내 생각으론 다음과 같다.
LCS[i][j] = str1은 str1[i]로, str2는 str2[j]로 끝나는 최장공통문자열말이 복잡한데, 비교하는 두 문자가 같은지 다른지에 따라 경우의 수를 나누어서 정리하면 이렇다.
if str1[i] == str2[j] == 'X':
LCS[i][j] = str1과 str2를 비교했을 때 'X'로 끝나는 최장공통문자열
('X'가 앞에서부터 만들어진 최장공통문자열의 뒤에 붙을지,
새로운 최장공통문자열의 시작이 될지는 이전값을 통해 알 수 있다. => DP)
else:
LCS[i][j] = 애초에 끝자리가 다르므로 최장공통문자열일 수가 없음 (즉, 0)(2) 예시
str1 = GBCDFE
str2 = ABCDEF
str1[3] == str2[3] == 'C'이므로,LCS[3][3]에는 GBC와 ABC를 비교해서 C로 끝나는 최장공통문자열인 BC의 길이 2가 들어가게 된다.
cf) GB(C)와 AB(C)의 최장공통문자열 'B' + 'C' = 'BC'
str1 = GBCDFE
str2 = ABCDEF
- 반면
str1[4] != str2[5]이므로,LCS[4][5]에는 GBCD와 ABCDE를 비교했을때 각각 D와 E로 끝나는 최장공통문자열이란 존재할 수 없으므로 0이 들어가게 된다.
(3) 그림으로 보는 동작과정
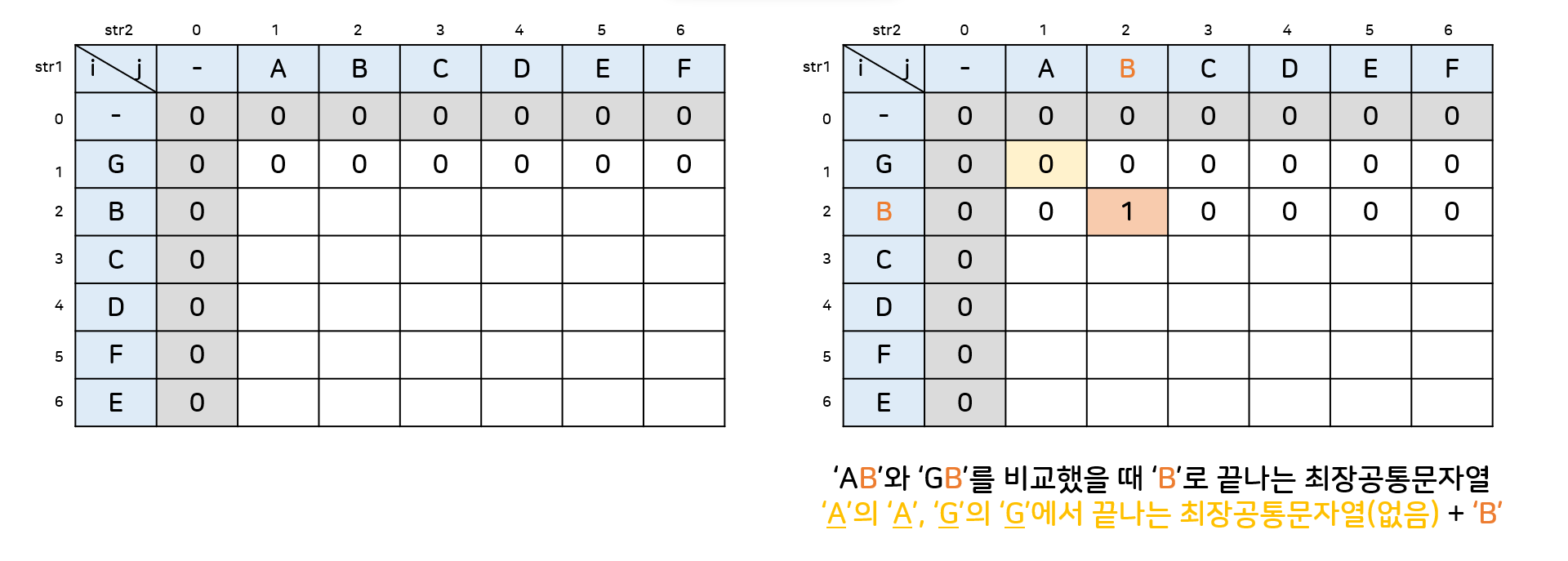
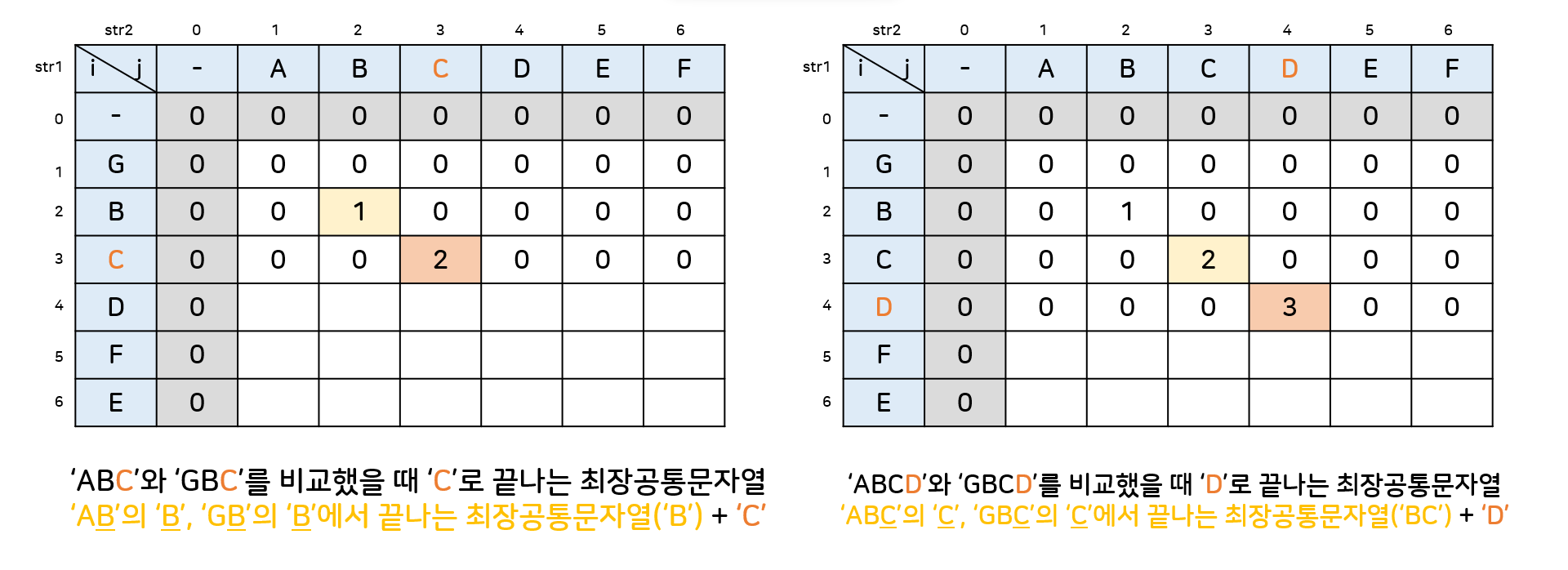

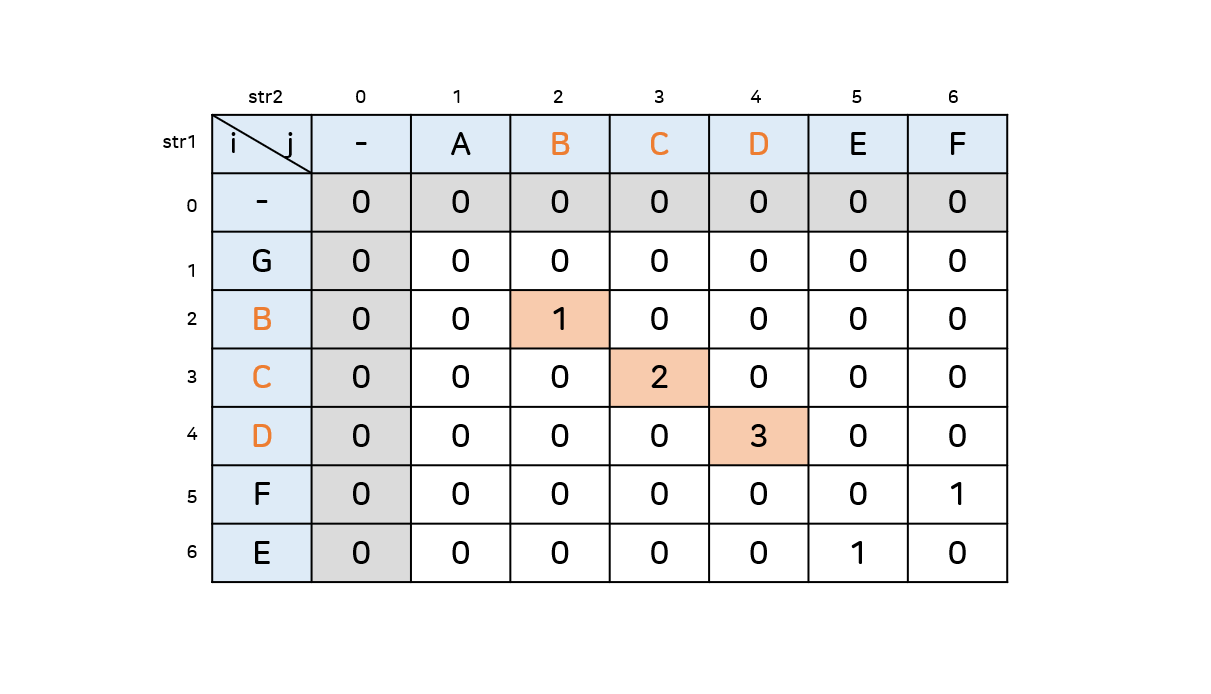
쉽게 말하자면 현재 비교하고 있는 문자가 똑같을때, 각 문자열의 현재 문자의 바로 앞에 있는 문자가 이미 만들어져있는 최장공통문자열의 일부인지 보고, 일부이면 그 뒤에 붙이고, 아니라면 이 문자를 새로운 최장공통문자열의 시작으로 보는 것이다. 어쨌든 후자의 경우에도 0(없음)에서 1(현재문자)을 더하는 점에서 똑같기 때문에, LCS[i][j] = LCS[i-1][j-1]+1이라는 식이 성립하는 것이다.
(4) 코드
코드로 나타내면 다음과 같다.
LCS = [[0 for _ in range(len(str2)+1)] for _ in range(len(str1)+1)]
for i in range(1, len(str1)+1):
for j in range(1, len(str2)+1):
if str1[i-1] == str2[j-1]:
LCS[i][j] = LCS[i-1][j-1] + 1
else:
LCS[i][j] = 0
# LCS의 최대값이 최장공통문자열의 길이2. 최장 공통 부분수열
최장 공통 문자열과 알고리즘은 같은데, 두 문자가 다를 때 처리하는 방식이 다르다. 최장 공통 부분수열은 두 문자가 다를 때도 이를 건너뛰고 LCS를 이어갈 수 있기 때문에, 0으로 퉁치는게 아니라 추가적인 식이 필요하다.
(1) LCS에는 무슨 값이 들어가는가?
이번에는 LCS에 담는 내용이 (비교적?) 직관적이다.
LCS[i][j] = str1[0:i]과 str2[0:j]의 최장공통부분수열
(다만, 최장공통문자열과는 달리
최장공통부분수열의 끝이 str1[i]나 str2[j] 이전에 위치한 문자일 수 있다.)마찬가지로 비교하는 두 문자가 같은지 다른지에 따라 경우의 수를 나누어서 정리하면 다음과 같다.
if str1[i] == str2[j] == 'X':
LCS[i][j] = str1[0:i]와 str2[0:j]의 최장공통부분수열 + 'X'
else:
LCS[i][j] = max(str1[0:i]와 str2의 최장공통부분수열, str1와 str2[0:j]의 최장공통부분수열)-
만약
str1[i] == str2[j]라면, 현재 문자를 제외한 이전 문자열들끼리 비교해서 구한 최장공통부분수열에 현재 문자를 더하면 된다. -
그런데
str1[i] != str2[j]라면? 현재 문자는 최장공통부분수열에 넣을 수 없지만, 현재 문자를 그냥 건너뛰고 다음에 더 이어갈 수 있으므로, 이전에 구한 최장공통부분수열 중 가장 큰 값을 복사해놓으면 된다.여기서 '이전에 구한 최장공통부분수열'이란,
str1[0:i]과str2의 최장공통부분수열, 또는str1과str2[0:j]의 최장공통부분수열이다.
(2) 예시
str1 = GBCDFE
str2 = ABCDEF
str1[3] == str2[3] == 'C'이므로,LCS[3][3]에는 GBC와 ABC의 최장공통부분수열인 BC의 길이 2가 들어가게 된다.
cf) GB(C)와 AB(C)의 최장공통부분수열 'B' + 'C' = 'BC'
str1 = GBCDFE
str2 = ABCDEF
- 반면
str1[3] != str2[2]이므로,LCS[3][2]에는 GBC와 AB의 최장공통부분수열이 들어가되 각각 C와 B는 포함하지 않은 값이 들어갈 것이다. 이때 이전에 구한 GB와 AB의 최장공통부분수열, GBC와 A의 최장공통부분수열 중 큰 값이 들어간다.
(3) 그림으로 보는 동작과정



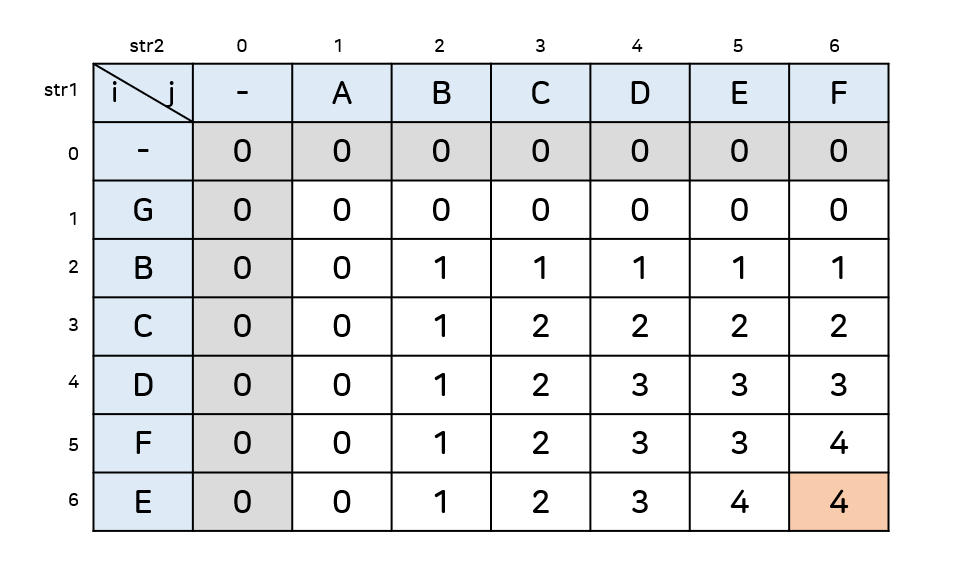
ㅋㅋㅋㅋ 내가 그려놓고도 세상 정신없다
아무튼 가장 마지막값([-1][-1])이 최장공통부분수열의 길이다.
(4) 코드
LCS = [[0 for _ in range(len(str2)+1)] for _ in range(len(str1)+1)]
for i in range(1, len(str1)+1):
for j in range(1, len(str2)+1):
if str1[i-1] == str2[j-1]:
LCS[i][j] = LCS[i-1][j-1] + 1
else:
LCS[i][j] = max(LCS[i][j-1], LCS[i-1][j])
print(LCS[-1][-1])(5) LCS 실제 값 찾기
- LCS의 가장 마지막값(
LCS[-1][-1])부터 시작한다. LCS[i-1][j]와LCS[i][j-1]중 같은 값이 있으면 해당 위치로 이동한다.- 같은 값이 없으면 해당 위치의 문자를 결과에 저장하고,
LCS[i-1][j-1]로 이동한다. LCS[i][j]가 0이 될 때까지 2~3번 과정을 반복한다.- 탐색을 종료하고 결과를 뒤집으면 실제 LCS의 값이다.
result = []
i = len(str1)
j = len(str2)
while dp[i][j] > 0:
if dp[i-1][j] == dp[i][j]:
i -= 1
elif dp[i][j-1] == dp[i][j]:
j -= 1
else:
result += str1[i-1]
i -= 1
j -= 1
result.reverse()
print("".join(result))Reference
[알고리즘] 그림으로 알아보는 LCS 알고리즘 - Longest Common Substring와 Longest Common Subsequence
