
대충 이분탐색인 것까지는 예상을 했는데(딱 봤을 때 골드5에서 브루트포스는 아닐거고, 그래프도 아니고, dp도 아니고, 그리디도 아니고, 스택/큐/힙도 아니고, 그럼 남은건 이분탐색이니까), 잘 안돼서 진짜진짜 마지막으로 이것만 보자는 마음으로 알고리즘 분류를 눌렀는데 투포인터...는 초면이네? (아직도 새로운게 나와.. 엉엉)
(스포 : 이분탐색만으로도 풀 수 있었는데 난 못했다.. 바보다)
투포인터
말그대로 2개의 포인터를 이용해서 문제를 해결하는 알고리즘이다.
1차원배열에서 두 개의 포인터를 이용해 탐색하면서 원하는 결과를 얻는데, 반복문을 사용한 기존의 방식보다 시간과 메모리의 효율성을 높일 수 있다.
투포인터의 종류
-
앞에서 시작하는 포인터와 끝에서 시작하는 포인터가 만나는 형식

-
빠른 포인터가 느린 포인터보다 앞서가는 형식

문제에 따라 어떤 포인터를 쓸지 잘 생각해봐야 한다.
동작과정(예시)
투포인터에 대해 찾아보다가 한방에 이해가 잘됐던 문제다.
수열
A[1], A[2], …, A[N]의i번째 수부터j번째 수까지의 합A[i] + A[i+1] + … + A[j-1] + A[j]가M이 되는 경우의 수를 구하시오.
M=5일때의 동작과정을 보자.
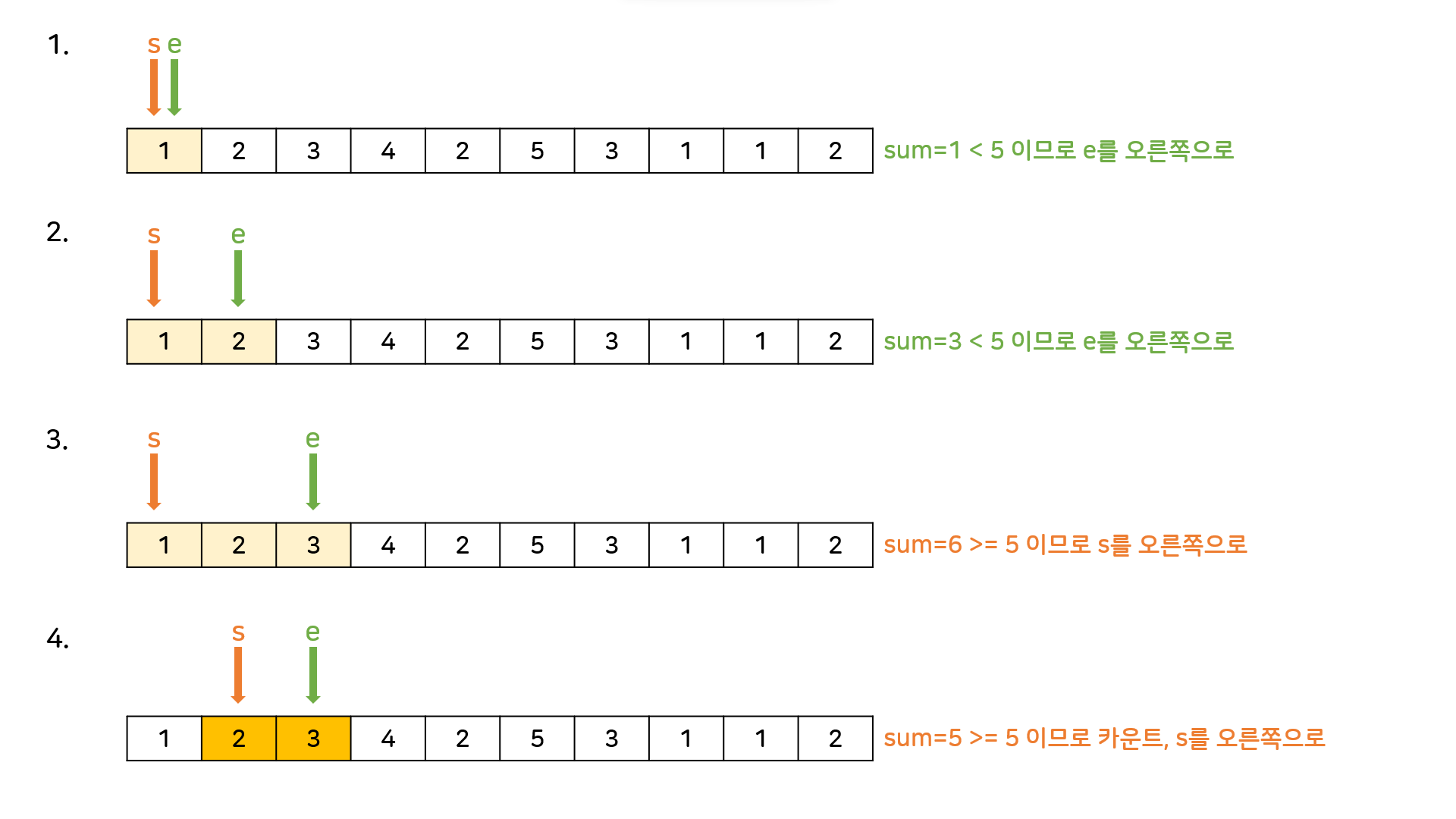
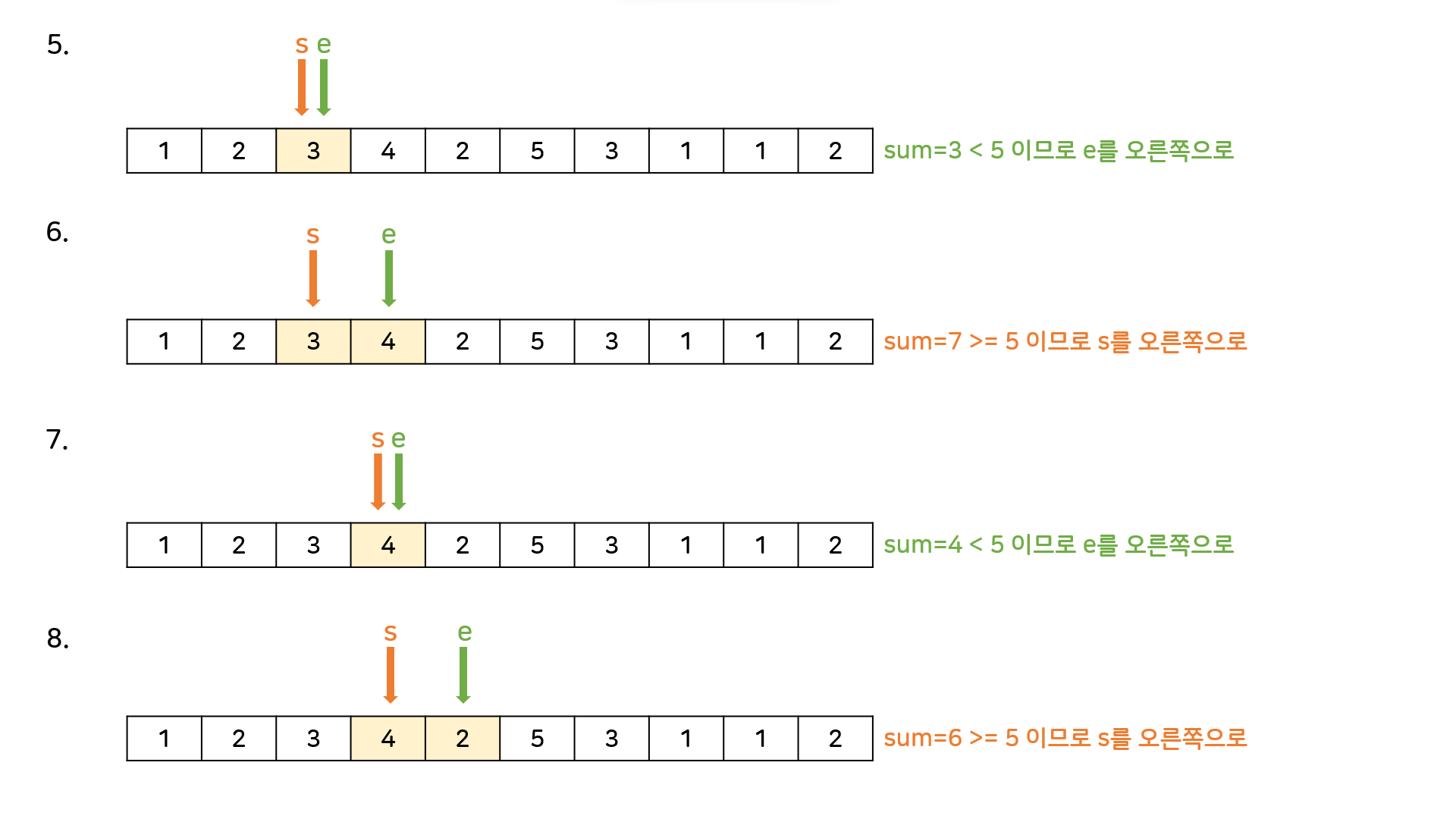
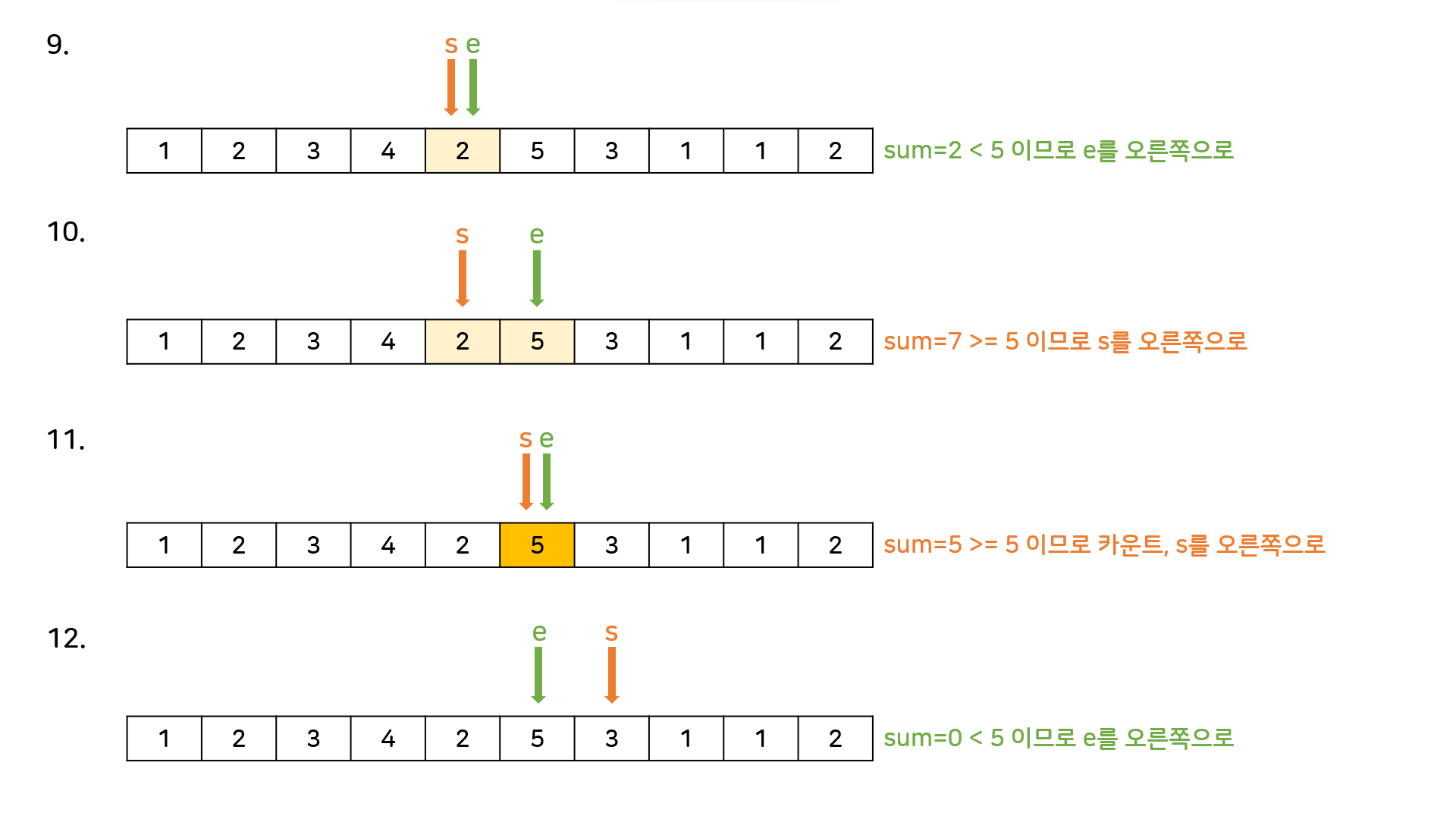
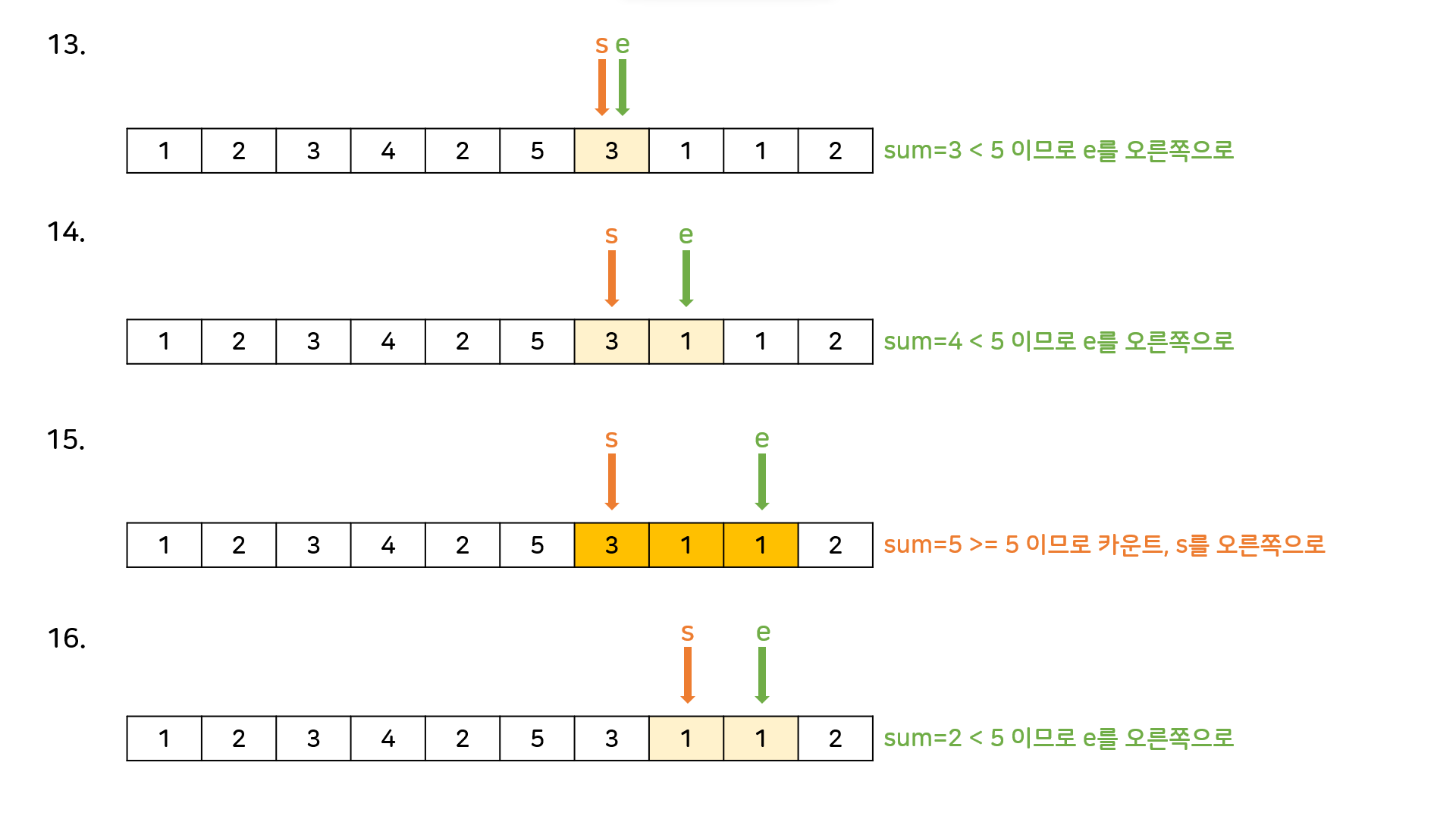
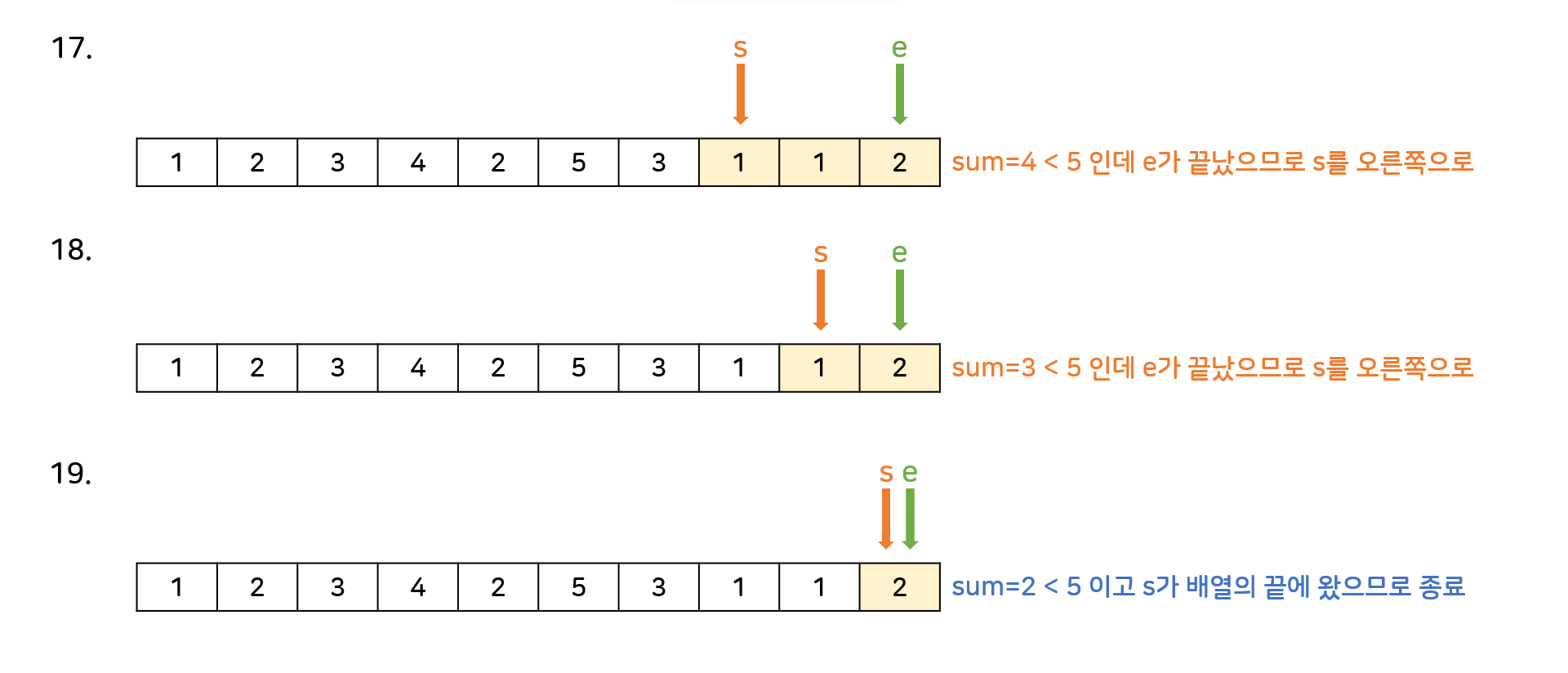
e를 증가시키는 것은 더할 수를 늘리는 것이고, s를 증가시키는 것은 더할 수를 줄이는 것이다. 문제상황에 따라 적절히 변형하면 된다.
이렇게 투포인터 알고리즘을 사용하면 반복문을 매번 돌리지 않아도 O(N)의 시간복잡도로 문제를 해결할 수 있다.
투포인터 알고리즘을 이용하면 모든 경우의 수를 셀 수 있으며, 꼭 배열이 정렬되어 있지 않아도 사용 가능하다.
[2467] 용액 코드
투포인터 ver.
import sys
input = sys.stdin.readline
N = int(input())
sol = list(map(int, input().split()))
p1 = 0
p2 = N-1
s = 2000000000
while p1 < p2:
mix = sol[p1]+sol[p2]
if abs(mix) < abs(s):
answer = [sol[p1], sol[p2]]
s = mix
if mix < 0:
p1 += 1
else:
p2 -= 1
print(answer[0], answer[1])포인터 종류는 앞에서 시작하는 포인터와 끝에서 시작하는 포인터가 만나는 형식이다.
두 포인터가 가리키는 값의 합이 최소값이면 정답을 갱신한다.
두 포인터가 가리키는 값이 음수일때는 0에 가까워지기 위해서는 수를 키워야하니까 앞포인터를 늘리고, 양수일때는 0에 가까워지기 위해 수를 줄여야하니까 뒤포인터를 줄인다.
번외) 이진탐색 ver.
이진탐색은 뭘까 싶어서 찾아봤더니 이렇게 모든 용액에 대해서 내 다음 용액부터 끝까지를 범위를 잡고 이진탐색을 총 n-1번 수행하는 방법도 있었다. 큰틀은 투포인터랑 매우 비슷하다.
(안돌려봄 그냥 로직만 참고)
import sys
input = sys.stdin.readline
N = int(input())
sol = list(map(int, input().split()))
s = 2000000000
for i in range(n-1):
current = sol[i]
start = i + 1
end = n - 1
while start <= end:
mid = (start + end) // 2
mix = current + sol[mid]
if abs(mix) < abs(s):
answer = [sol[p1], sol[p2]]
s = mix
if mix < 0:
start = mid + 1
else:
end = mid - 1
print(answer[0], answer[1])