[코테] 백준 class 4 완료 & 정리

🗓️ 2023.08.09 ~ 2023.08.21

점점 어려운 것만 나오다 보니까 중간에 슬럼프가 와서 하기 싫어서 좀 놨다.. 힘들었다.. 답도 엄청 많이 봤고 알고리즘 분류도 숨겨놨다가 툭하면 눌러서 봤고 풀었다고 하기에도 민망한 수준이다.

클래스4에서는 백트래킹, 트리, 최단 거리 알고리즘(데이크스트라 등), 분리 집합, LIS, LCS, 누적 합, 배낭 문제가 새로 등장했다.

레벨은 문제보다 알고리즘 자체의 난이도가 골드인 느낌

하나하나 공부하면서 푸느라고 더 늦어진 감도 있고...

갈수록 처음보는것만 산더미라서 의욕이 점점 사라졌다.. 정말 어렵다ㅜ

---

📌 LIS(최장 증가 부분 수열), LCS(최장 공통 부분 수열), 트리 순회, 누적합(2차원), 배낭문제, 0-1 BFS, 분할정복, 트리의 지름(트리에서 경로찾기), 백트래킹(Backtracking), 벨만포드

📌 음의 사이클 찾아내기 (시작지점이 없는 벨만포드)
-[1865] 웜홀
원래 벨만포드라면 값을 갱신하기 전에 distance[start] != INF 조건이 있어야하는데, 얘는 이 조건을 빼야 통과가 됐다. 이 조건을 빼면 시작지점과 관계없이 벨만포드 알고리즘이 진행되는데, 그러면 distance는 더이상 '시작지점으로부터의 최단거리 테이블'이 아니라 '음수 사이클의 존재 유무를 판단하는 테이블'이 된다.
cf) distance[start] != INF 조건은 시작지점을 정했을때, 이 시작지점으로부터 이어진 노드의 최소거리를 구하기 위해 있는 거였다. (distance[start]=0 초기화 후 distance[cur] != INF 조건이 있어야 시작지점부터 연결된 노드를 찾을 수 있기 때문)

📌 BFS에서 최단경로의 경우의 수가 여러가지일 때
-[2206] 벽 부수고 이동하기
벽을 부쉈는지, 안부쉈는지에 따라 최단경로가 여러개가 되기 때문에 처음에는 DFS+백트래킹으로 풀려고 했으나 "최단거리"를 찾아야 하기 때문에 가능한 모든 경로를 찾는 DFS로는 시간초과가 났다. 그래서 BFS로 풀어야만 했는데, 벽 부수기 여부를 어떻게 나타낼까 하다가 구글링해봤더니 대부분 visited[x][y][z]꼴로 3차원배열을 쓰고 있었다. visited[x][y][0]은 벽을 부수지 않은 경로, visited[x][y][1]은 벽을 부순 경로를 나타낸다. 이렇게 최단경로를 구해야하는데 경우의 수가 나누어지는 경우, 방문여부를 나타내는 visited를 더 고차원의 배열로 쪼개서 각각 활용할 수 있다는 점을 알았다.

📌 [1918] 후위 표기식
모르겠어서 그냥 답 보고 풀었다 이해도 하기 귀찮다... 다음에 다시 보자

---

[1149] RGB거리

DP는 맨날 문제 보고 아 DP구나 알긴 알겠는데 그래서 DP로 어떻게 푸는지를 감을 못잡겠다....

이번에는 특히 알고리즘은 DP일거라고 예상해두고 정작 구현은 그리디로 하려고 해서 제대로 시작도 못했다.

이 문제를 풀면서 약간.. 내가 오해하고 있었던? 헷갈리는? 부분을 다시 짚어보려고 한다.

❗💡 DP는 큰 문제를 작은 문제를 쪼갰을때, 작은 문제 중에 답일 것 같은 문제 몇 개만 선택해서 구하는게 아니라(이건 탐욕법) 모든 작은 문제들을 풀어서 큰 문제를 향해 나아가는 것!!!! 오히려 그리디보다 완전탐색에 가깝다고 볼 수 있다.(뇌피셜) 헷갈리지 말고 모든 작은 문제를 고려하는게 맞는거니까 비효율적이라고 생각하지 말기!!!! 💡❗

⭐ 첫번째 선택을 뭘로 해야할지 모르겠다? => 첫번째로 선택할 수 있는 모든 경우를 고려해야 하니까 당연함 ⭐

따라서 이 문제의 풀이는 두번째 집부터 시작해서,

1. 현재집을 빨간색으로 칠하는 비용 + 이전집이 초록색 / 파란색인 경우 중 작은 비용
2. 현재집을 초록색으로 칠하는 비용 + 이전집이 빨간색 / 파란색인 경우 중 작은 비용
3. 현재집을 파란색으로 칠하는 비용 + 이전집이 빨간색 / 초록색인 경우 중 작은 비용

위의 식을 활용해 현재집을 각각 빨간색/초록색/파란색으로 칠했을 때의 최소비용을 구한다.

마지막 집에 대해 위에서 구한 세 비용 중 최소값을 출력하면 답이다.

N = int(input())
rgb = []
for _ in range(N):
  r, g, b = map(int, input().split())
  rgb.append([r,g,b])

i = 0
for r, g, b in rgb[1:]:
  rgb[i+1][0] += min(rgb[i][1], rgb[i][2]) # r
  rgb[i+1][1] += min(rgb[i][0], rgb[i][2]) # g
  rgb[i+1][2] += min(rgb[i][0], rgb[i][1]) # b
  i += 1

print(min(rgb[-1]))

DP랑 그리디랑 헷갈리지 말기

---

[9465] 스티커

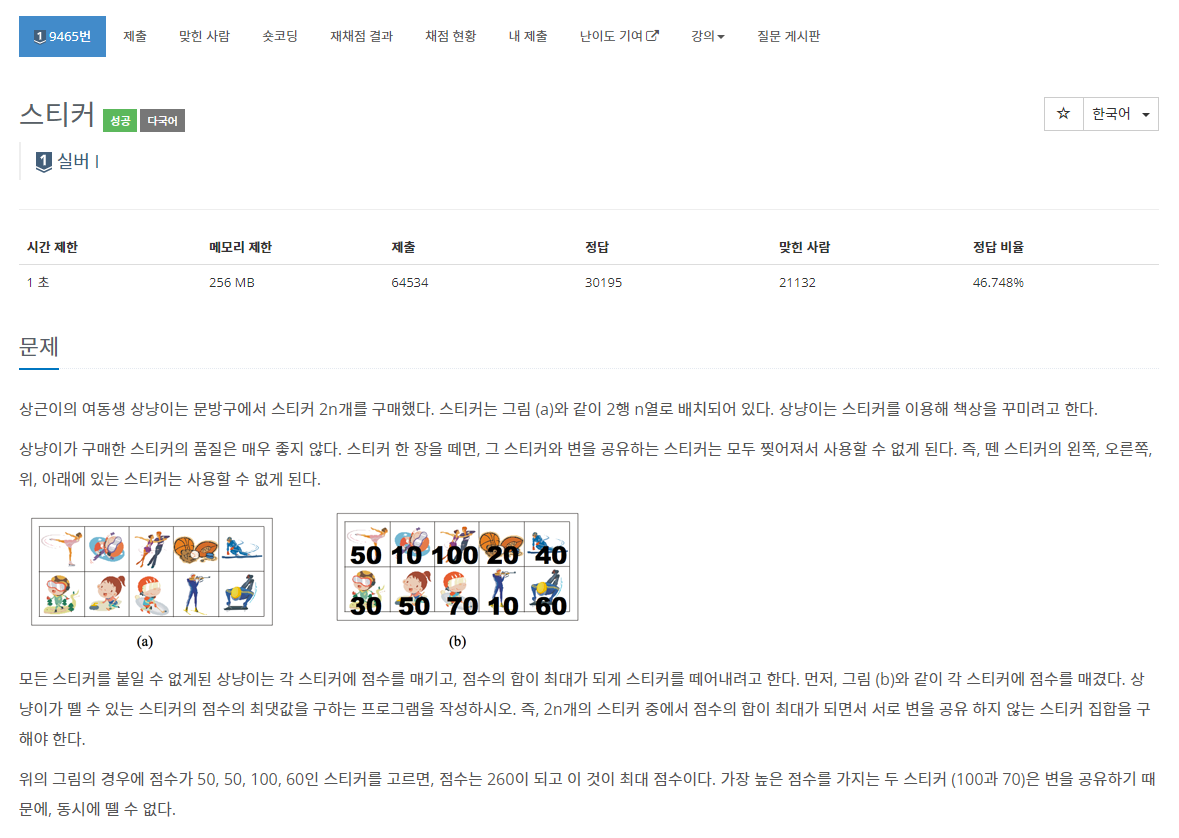
얘는 틀린건 아니고 처음으로 제대로 푼 DP 문제 같아서 복기하려고 들고왔다! ╰(°▽°)╯

내 생각의 흐름을 그대로 적어보자면

1. 최댓값 구하기 & 첫번째로 뗄 스티커가 뭔지 모르겠음 => DP 인가보구나
2. dp[x] = 2x개의 스티커 중에서 두 변을 공유하지 않는 스티커 점수의 최댓값
3. 큰 문제(2행 n열) -> 작은 문제(2행 1열)로 쪼개기
4. 매 차례에서 가능한 선택의 종류는? => 위쪽 스티커 선택 or 아래쪽 스티커 선택 or 아무것도 선택X
5. 위쪽 스티커를 선택하려면 이전에 아래쪽 스티커를 선택하거나 아무것도 선택X
   아래쪽 스티커를 선택하려면 이전에 위쪽 스티커를 선택하거나 아무것도 선택X
   아무것도 선택하지 않을때는 제한조건 없음
6. 이전에 가능한 경우 중 큰 점수 선택

import sys
input = sys.stdin.readline

T = int(input())
for _ in range(T):
  n = int(input())
  sticker1 = list(map(int, input().split()))
  sticker2 = list(map(int, input().split()))

  dp = [(0, 0, 0)]
  idx = 0
  for s1, s2 in zip(sticker1, sticker2):
    choice1 = max(dp[idx][1], dp[idx][2]) + s1
    choice2 = max(dp[idx][0], dp[idx][2]) + s2
    choice0 = max(dp[idx])
    dp.append((choice1, choice2, choice0))
    idx += 1

  print(max(dp[-1]))

💡 작은 문제로 쪼개고!
💡 선택할 수 있는 모든 경우의 수를 구해보기!

---