
하도 오랜만에 공부하려니 헷갈려서 정리
DFS/BFS와 백트래킹
1. DFS/BFS
: 시작점 고정, 돌아나오기 X
2. 백트래킹
: 시작점 여러개로 설정 가능, 돌아나오기 O
=> 이때 backtracking 함수 내에서 for문 탐색 범위 설정만으로 시작점 여러개 지정 가능 + 메인함수에서 호출은 backtracking(0) 한번으로 끝 (순열코드 참조)
순열/조합과 백트래킹
1. 순열/조합
itertools못쓰게 하는 경우
=> 백트래킹 문제 (어려움)itertools쓸 수 있는 경우
=> 구현 문제 (쉬움)
2. 백트래킹
- 순열/조합
- 현재 상태에 무관하게 모든 경우를 다 보는 경우
=>itertools대체 가능, 쉬운 구현 문제로 변환 가능 - 현재 상태에 따라 다음에 선택할 수 있는 경우가 달라지는 경우
=>itertools대체 불가능, 진짜 백트래킹 문제
- 현재 상태에 무관하게 모든 경우를 다 보는 경우
- 그 외 : 아직 그런 문제는 못 봄
itertools 안쓰고 itertools 구현하기
#현재 상태에 무관하게 모든 경우를 다 보는 경우
#라이브러리 쓰면 쉬운 구현문제인데 못써서 백트래킹 문제로 어려워진 경우
1. 백트래킹으로 순열 구하기
1,2,3 != 3,2,1이므로 이전에 방문했던 곳도 재방문해야함
=>visited방문여부 표시 필요 O- 종료조건 :
depth == 찾으려는 개수 - 탐색범위 : 매번 처음부터 끝까지
- 재귀호출 :
permutation(depth+1)
num_list = [1,2,3,4,5]
visited = [False for _ in range(len(num_list))]
perm = []
r = 3 # 3개 뽑기
def permutation(depth):
if depth == r:
print(perm)
return
for i in range(len(num_list)):
if visited[i] == False:
visited[i] = True
perm.append(num_list[i])
permutation(depth+1)
perm.pop()
visited[i] = False
permutation(0)[1, 2, 3]
[1, 2, 4]
[1, 2, 5]
...
[2, 4, 3]
[2, 4, 5]
[2, 5, 1]
...
[5, 4, 1]
[5, 4, 2]
[5, 4, 3]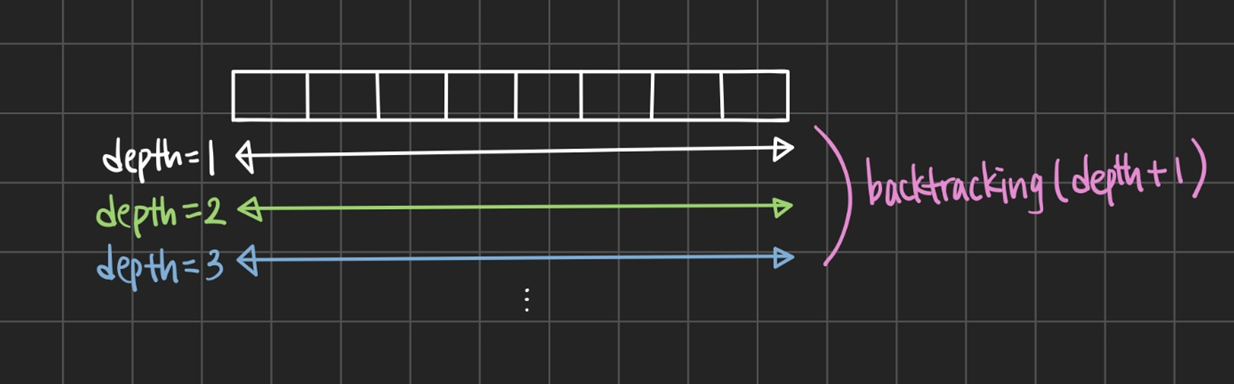
2. 백트래킹으로 조합 구하기
1,2,3 == 3,2,1이므로 이전에 방문했던 곳은 재방문할 필요 없음
=>visited방문여부 표시 필요 X- 종료조건 :
depth == 찾으려는 개수 - 탐색범위 : 나부터 끝까지 (내 앞은 안봄)
- 재귀호출 :
combination(i+1, depth+1)
num_list = [1,2,3,4,5]
comb = []
r = 3 # 3개 뽑기
def combination(start, depth):
if depth == r:
print(comb)
return
for i in range(start, len(num_list)):
comb.append(num_list[i])
combination(i+1, depth+1)
comb.pop()
combination(0, 0)[1, 2, 3]
[1, 2, 4]
[1, 2, 5]
[1, 3, 4]
[1, 3, 5]
[1, 4, 5]
[2, 3, 4]
[2, 3, 5]
[2, 4, 5]
[3, 4, 5]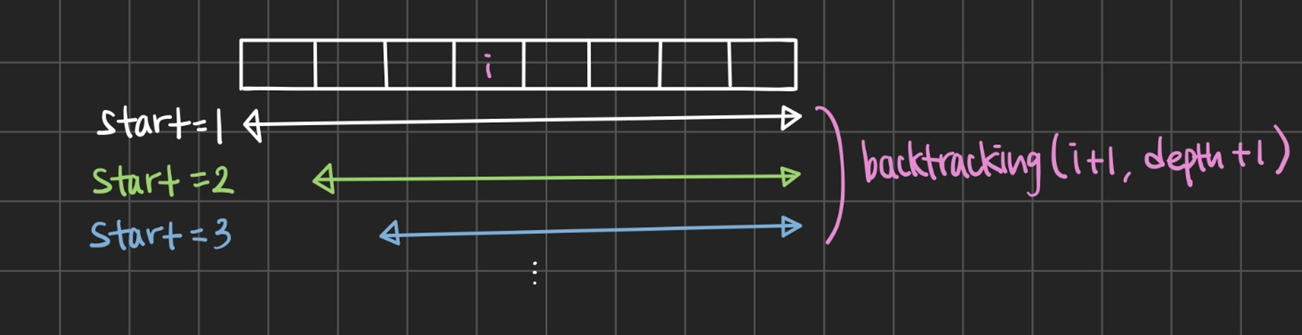
itertools 쓸 수 있든 없든 백트래킹으로 풀어야하는 문제
#이건 그냥 파이팅할 일이네요
문제의 큰 틀이 순열인지 조합인지 확인한다.
-
조합
- 순서 상관없이 뽑기만 하면 되는 경우
- 이전꺼는 볼 필요 없음
- 재귀가 깊이 들어갈수록 탐색범위 줄어들어야함
- 파라미터에 현재상태 저장해두고 "나 다음에 있는 것만 보도록" 탐색범위 줄이는데 활용하기
-
순열
- 순서 상관 있음
- 이전 것도 봐야함
- 재귀가 깊이 들어가도 탐색범위 그대로
- 처음부터 끝까지 다 확인할 것
ex. 사다리조작

자세한 풀이는 생략
사다리를 놓을 수 있는 가로선 위치 (최대) 3개를 골라야 한다.
=> 순서는 상관없다
=> 조합
=> 나 다음에 있는 것만 보기
import sys
input = sys.stdin.readline
def check():
global H, ladder
for k in range(1, N+1):
now = k
for h in range(1, H+1):
if ladder[h][now] == 1:
now += 1
elif ladder[h][now] == 2:
now -= 1
if now != k:
return False # k번째 세로선이 k번에 도달하지 않음
return True
def set_garo(cnt, x, y): #❗1. x행 y열부터 사다리를 놓아볼 것임❗
global ladder, H, N, answer
if check(): # 정답
answer = min(answer, cnt)
return
elif cnt >= 3 or cnt >= answer:
return
for i in range(x, H+1): #❗2. 나(x행) 이후부터 탐색❗
k = y if i == x else 0 #❗3-1. x행 가로선에서는 y열부터 (x행 y열, 즉 중간부터 탐색)❗
#❗3-2. 그 다음 가로선부터는 0열부터❗
for j in range(k, N): #❗4. 나(k열) 이후부터 탐색❗
if ladder[i][j] == 0 and ladder[i][j+1] == 0:
ladder[i][j] = 1
ladder[i][j+1] = 2
set_garo(cnt+1, i, j+2) #❗5-1. 이번에 사다리를 놓은 곳 i행 j열❗
#❗5-2. 이후 탐색은 i행 j+2열부터 진행❗
#❗5-3. j+1열은 어차피 못놓으니까 패스❗
ladder[i][j] = 0
ladder[i][j+1] = 0
return
def solution():
global H, ladder, N, answer
N, M, H = map(int, input().split())
ladder = [[0 for _ in range(N+1)] for _ in range(H+1)]
for _ in range(M):
a, b = map(int, input().split())
ladder[a][b] = 1
ladder[a][b+1] = 2
answer = 1e9
set_garo(0, 1, 1)
if answer == 1e9:
print(-1)
else:
print(answer)
return
if __name__ == "__main__":
solution()근데 이렇게 탐색범위 줄여도 파이썬으로는 시간초과나서 pypy3으로 제출함ㅋ
