🗓️ 2023.08.21 ~ 2023.09.08 🗓️
3주.... 드디어 처음에 목표했던 클래스5+까지 다 풀었다.
정말 오질나게 어려웠고 중간에 정말 딥빡&현타&우울&짜증으로 포기하고 싶었는데 어찌저찌 했네

DP가 정말 사람 빡치게 한다 봐도봐도 모르겠다 비트필드DP할 때는 진짜 노트북 부숴버리고 싶었다
이번에 새로운 알고리즘이라 몰라서 못푼거 말고 그냥 못풀어서 정리한 문제도 하나 빼고 죄다 DP다 (╬▔皿▔)╯
🍂
이제 코테에 어느정도 감이 온거 같아서 회고 겸 정리해본다.
코테 공부 시작한지 오늘로 75일이다. 2달반 정도? 프로그래머스로 한달, 백준으로 한달반
엄청 오래한 거 같은데 석달도 안됐다.. 이번에 코테탈하면 꼴랑 석달만 공부해서 떨어진거라고 자기합리화해야지
그동안 유의미하게 푼 문제는 다 합쳐서 한 200개 정도 되는거 같다.
이제 개강도 해서 그동안 한 것만큼 빡세게는 못하겠지만 앞으로 매일 1~2개씩 푸는게 목표다. (다음 목표는 기업 기출 풀기)
문제 보고 적용할 알고리즘 잘 유추해내는 거랑 시간복잡도, 공간복잡도 생각하면서 푸는 연습을 해야될 것 같다.
엄청 더운 여름에 시작했는데 이제 벌써 가을이고 개강도 했다..
📌 투포인터, 중간에서만나기, 비트필드를 이용한 DP, 백트래킹 시간복잡도 줄이기, 외판원의순회, 구현/시뮬레이션, LIS 역추적
📌 파이썬 빠른 입출력 꼭 쓰기
import sys input = sys.stdin.readline이거 생각보다 있고 없고 차이가 굉장하다;;;
어차피 틀린 코드였지만 얘가 없을 때는 틀리기 전까지 완전 엉금엉금 올라갔는데 이거 쓰니까 바로 걍 슈슉 올라가더라
📌 신발끈공식 (다각형 면적 구하기)
-[2166] 다각형의 면적
와 진짜 언제적 신발끈공식...
📌 부분수열에 관해서
부분수열은 완전탐색이나 백트래킹으로 구할 수 있다. 하나하나 다 구해봐야한다는 말이다. 시간을 줄여야할 때도 별다른 알고리즘이 있는게 아니고 '중간에서 만나기'로 연산횟수를 줄이는거지 얘도 결국은 완전탐색이다. LCS나 LIS같은게 DP인거고, 그냥 부분수열의 합을 구하는건 그냥.. 그냥 완전탐색이다.
📌 DP에 대해서..
- 기본적으로 작은 문제로 쪼갰을 때, 마지막값을 중점적으로 생각해야하는 것 같다. 예를 들어
dp[i][j]라면 작은 문제의 길이가i일때 마지막값이j라든가.- 잘 모르겠으면 문제를 쪼갤 때 어떻게 쪼갰는지, 기준점이 되는 것들로 i와 j를 구성하는 쪽으로 생각해보자. 쪼갠 기준점으로 행과 열을 구성하면, 그 안의 값은 쪼개진 문제의 답이 들어가게 될 것이다. (웬만하면?)
- '이전값'을 사용해야하므로, dp배열을 채우는 순서도 잘 생각해봐야한다. (행부터 or 열부터 or 대각선으로 or DFS 탐색순서대로 등등)
📌 파이썬으로 시간초과날 때 pypy3으로 제출하기 (알고리즘이 맞을 때)
실전 코테에서는 못쓰겠지만.. 지금 중요한건 아니니까..
📌 방향그래프에서 사이클 찾기
-[9466] 텀 프로젝트
무방향그래프에서 사이클 찾는건 크루스칼에서 공부한 것처럼 하면 되는데, 방향그래프에서 사이클은 DFS로 직접 찾아봐야한다. 그리고 사이클을 직접 출력할때는 사이클을 찾은 그 순간에while과pop으로 바로바로 출력해줘야 시간초과가 안난다.visited = [방문여부] path = [현재까지 방문한 경로] cycle = [사이클 여부] next = 다음에 방문할 곳 if visited[next] == True and next in path and cycle[next] == False: while path: p = path.pop() cycle[p] = True if p == next: break
[1005] ACM Craft
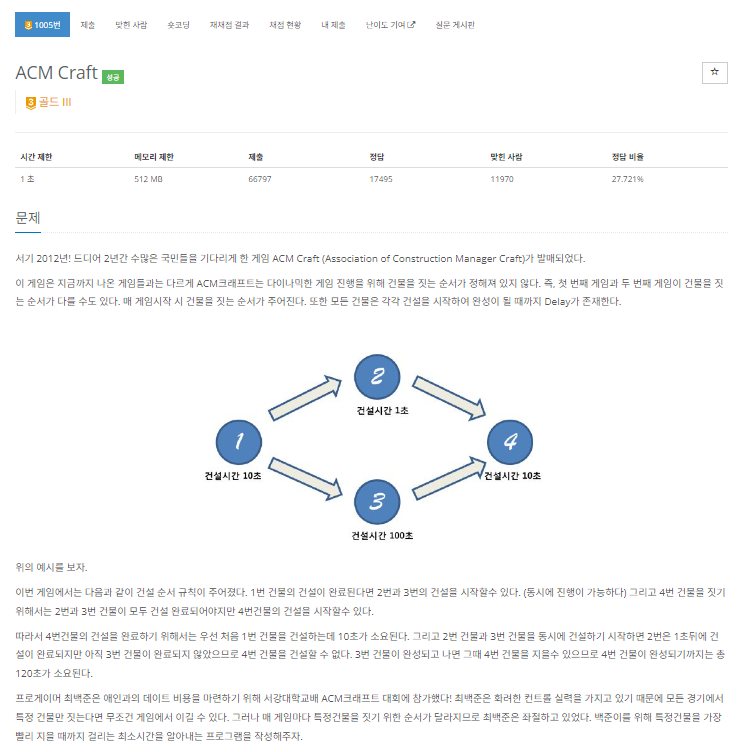
처음엔 BFS도 생각해보고 도착점부터 거꾸로 거슬러올라가는 것도 생각해봤는데 뭔가 딱 안맞아떨어졌다.
도저히 모르겠어서 알고리즘 분류를 보니 지금까지 공부한 것 중 유일하게(?아마도) 대충 넘어갔던 위상정렬이 뙇... 위상정렬은 처음이었으니까... 그럴 수 있지
근데 여기에 DP까지 포함될줄은 상상도 X ㅋ
작업순서는 위상정렬로 알고, 시간계산은 dp로 하는 문제였다.
위상정렬은 그냥 문제랑 그래프 생긴 것부터가 이마에 위상정렬이라고 써놓은 수준 그 자체였고
"이전에 있는 모든 작업을 완료한 후에 현재 작업 가능"까지는 생각해서 이게 "이전까지의 작업시간으로 현재 작업시간 계산"까지 이어졌으면 참 좋았겠지만 하루종일 고민했는데도 전~혀(ㅎ) 몰랐다.
어쨌든 키포인트는 위상정렬 알고리즘의 순서대로 작업을 하나씩 진행하는데, 이때 현재노드에 연결된 다음노드들의 진입차수를 1씩 줄이면서 dp[다음노드] = max(dp[다음노드], dp[현재노드]+D_list[다음노드])로 시간을 갱신해주고, 진입차수가 0이 되면 이 다음노드도 큐에 넣는거다.
import sys
input = sys.stdin.readline
from collections import deque
T = int(input())
for _ in range(T):
N, K = map(int, input().split())
D_list = [0]
D_list += list(map(int, input().split()))
graph = [[] for _ in range(N+1)]
indegree = [0 for _ in range(N+1)]
dp = [-1 for _ in range(N+1)]
for _ in range(K):
X, Y = map(int, input().split())
graph[X].append(Y)
indegree[Y] += 1
W = int(input())
queue = deque()
for i in range(1, N+1):
if indegree[i] == 0:
queue.append(i)
dp[i] = D_list[i]
while queue:
now = queue.popleft()
if now == W:
break
for g in graph[now]:
indegree[g] -= 1
if indegree[g] == 0:
queue.append(g)
dp[g] = max(dp[g], dp[now]+D_list[g])
print(dp[W])[10942] 팰린드롬?
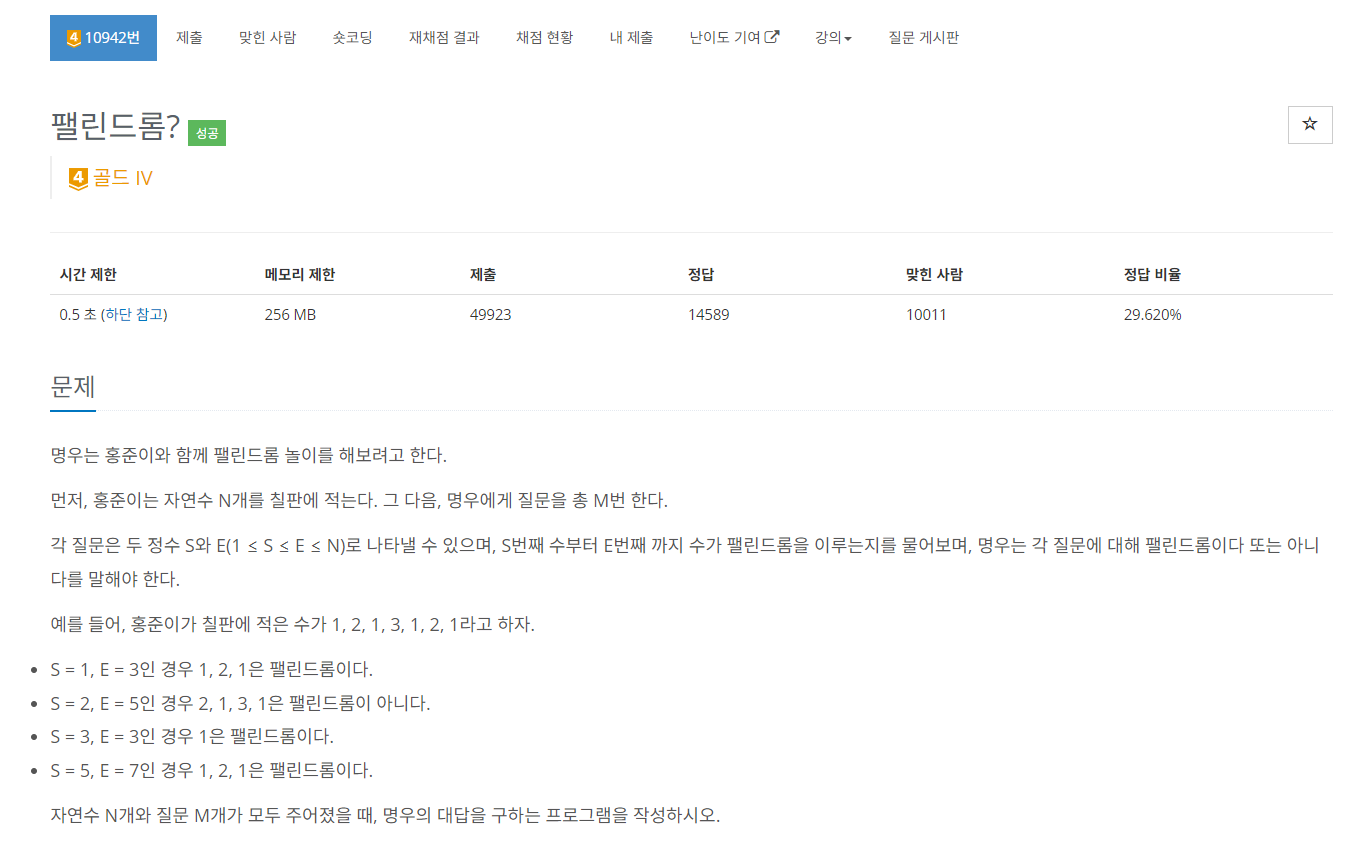
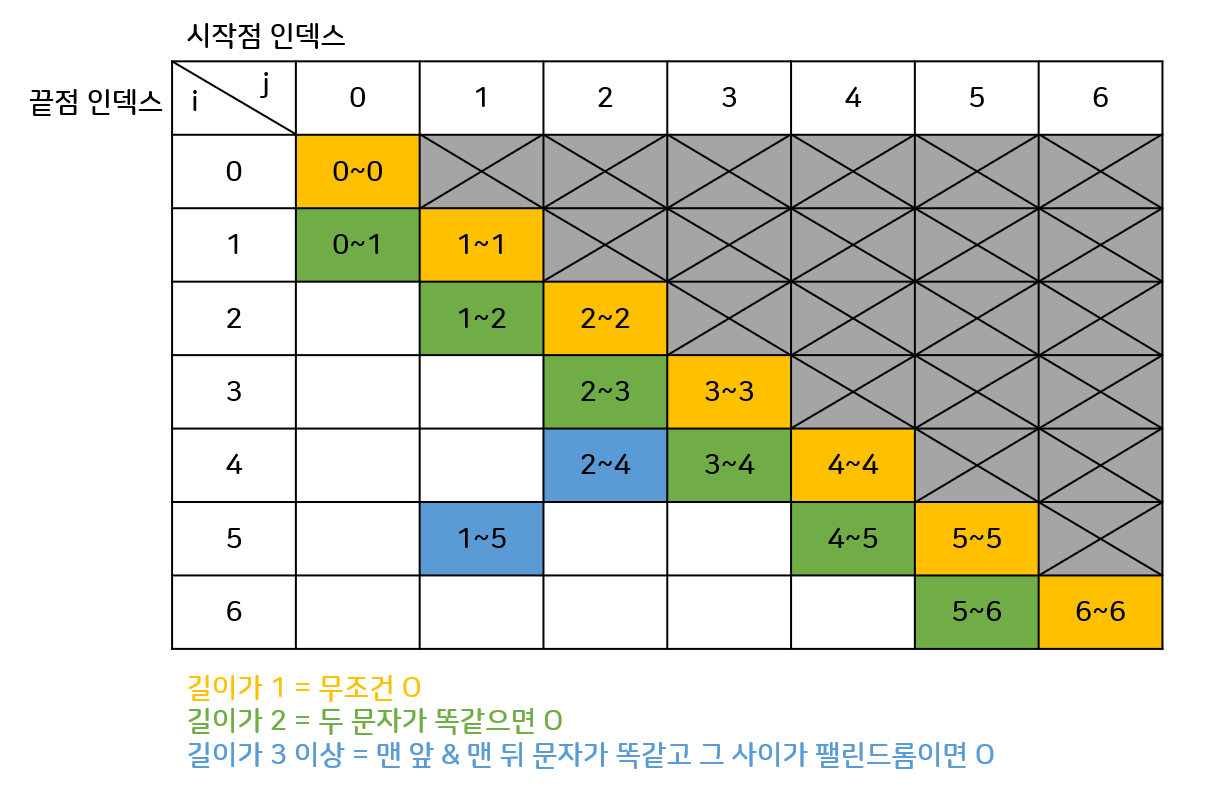
팰린드롬을 DP로 푸는구나...
import sys
input = sys.stdin.readline
N = int(input())
numbers = list(map(int, input().split()))
M = int(input())
questions = []
for _ in range(M):
S, E = map(int, input().split())
questions.append((S,E))
dp = [[0 for _ in range(N)] for _ in range(N)]
for i in range(N):
for j in range(i+1):
if i == j:
dp[i][j] = 1
elif i == j + 1:
if numbers[i] == numbers[j]:
dp[i][j] = 1
else:
if numbers[i] == numbers[j] and dp[i-1][j+1] == 1:
dp[i][j] = 1
for s, e in questions:
print(dp[e-1][s-1])하나의 수열(?)이 팰린드롬인지 확인하기 위해서 직접 확인하는 방법도 있고, 재귀로 확인하는 방법도 있는데, 모두 시간초과가 났다. DP로 계산하는 횟수를 줄이려고 해봤지만, 결론적으로 아예 해당 방법을 쓰지 않아야 시간초과가 나지 않았다.
배운점은 기존 풀이가 있는데 시간복잡도를 줄이기 위해 DP를 사용할 경우, 더 이상 그 풀이는 사용할 수 없다는 거다. DP는 정말 별다른 수식 없이 이전값을 이용해서만 풀어야 한다.
또한 계산순서나 인덱스를 알아서 잘 정해서, 반드시 "이전값"을 활용할 수 있도록 짜야한다는 것도 배웠다.
dp는 아직도 여전히 어렵다....
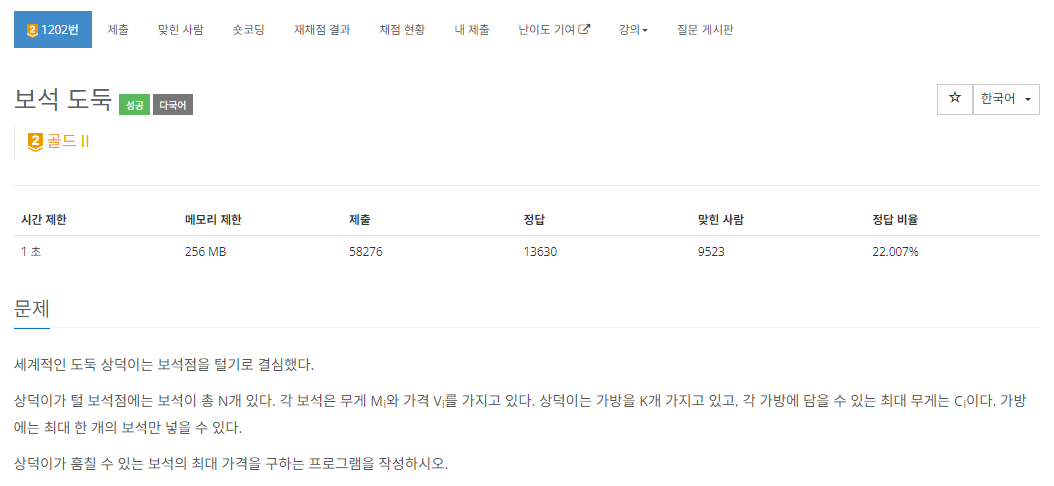
[1202] 보석 도둑
자료 구조, 그리디 알고리즘, 우선순위 큐, 정렬
진짜 진짜 풀이 안보고 싶었는데.. 하.. DP로 풀었더니 메모리초과가 났고 알고리즘을 보고 나서 어떻게든 풀려고 했는데 시간초과 진짜 개빡친다.
정답코드가 간단해서 더 짜증난다.
import sys
input = sys.stdin.readline
import heapq
N, K = map(int, input().split())
jewels = [list(map(int, input().split())) for _ in range(N)]
bags = [int(input()) for _ in range(K)]
jewels.sort() # 보석 무게순 오름차순 정렬
bags.sort() # 가방 무게순 오름차순 정렬
answer = 0
heap = []
i = 0
for b in bags: # 적게 들어가는 가방부터 하나씩 보면서
while i < N and jewels[i][0] <= b: # 넣을 수 있는 보석 모두 우선순위큐에 넣기
heapq.heappush(heap, -jewels[i][1]) # 최대힙
i += 1
if len(heap) > 0:
v = heapq.heappop(heap) # 우선순위 큐에 있는 값 중 가장 큰게 이번 가방에 들어갈 것임
answer += (v * -1)
print(answer)어차피 작은가방에 들어갈 수 있는 보석은 다음 큰 가방에도 들어갈 수 있기 때문에 굳이 확인하지 않아도 된다는게 시간이 초과되지 않는 중요 포인트다. 그래서 보석을 확인할 때 처음부터 보는게 아니라 이전에 마지막으로 본 보석부터 보기 시작한다.
[7579] 앱
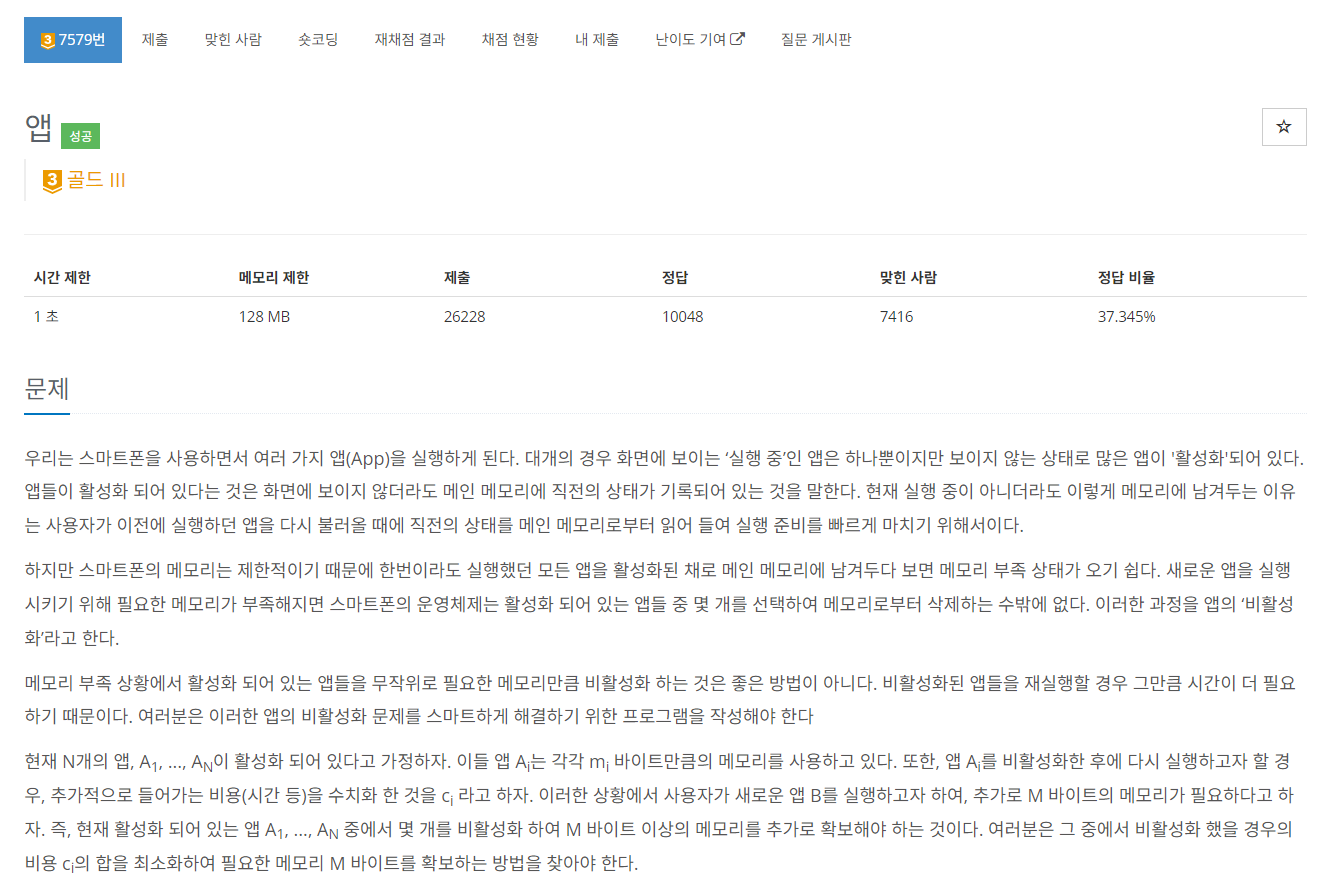
위 문제가 냅색인줄 알았는데 뜬금없이 얘가 냅색이었다. 처음엔 몰랐는데 알고보니 명칭만 다르고 대충 주어진 값 생김새가 냅색이랑 되게 비슷하다.
- 비워야하는 메모리 == 배낭 용량
(이후에 설명할거지만 이 문제에서 배낭용량은 사실 비용이다.) - 앱이 차지하는 메모리 == 보석의 무게
- 앱을 비활성화하는데 드는 비용 == 보석의 가치
차이점은 기존 냅색은 '배낭이 터지지 않게' 담아야 하는데, 이번에는 '메모리를 초과', 즉 배낭을 최소로 터지게 만들어야한다는 것이다.
그래서 처음엔 dp[고려할 앱][비울 수 있는 메모리]=이때의 최소비용으로 두고 풀었는데, 메모리 초과가 났다. (어라 라임이..)
이래저래 답은 나오는데 시간초과, 메모리초과가 자꾸 나서 찾아봤다.
dp[고려할 앱][사용한 비용]=비울 수 있는 메모리
dp[i][j] = i번째 앱까지 고려했을 때 비용 j로 얻을 수 있는 빈공간 메모리이렇게 바꾸니까 확실히 점화식 찾기도 딱딱 맞아떨어졌다. (기존 배낭문제와 동일한 로직)
i번째 앱의 비용이j보다 클 때
=>i번째 앱은 제외한다.
=>dp[i-1][j]i번째 앱의 비용이j보다 작거나 같을 때
=>i번째 앱을 포함하면dp[i-1][j-c_list[i]] + m_list[i]
=>i번째 앱을 제외하면dp[i-1][j]
둘 중 큰 값이 dp[i][j]가 된다.
💡 배운점 : 주어진 냅색문제가 배낭안에 넣는게 아니라 배낭을 터뜨리는 경우라면, '배낭'을 적절히 잘 설정해서 '배낭을 터뜨리지 않는' 방향으로 값을 채워나가야 한다.
이번에도 '배낭'을 '비워야하는 메모리'로 설정하면 배낭을 터뜨리는 것이지만, '비용'으로 설정하면 배낭을 터뜨리지 않는 것인거처럼 말이다.
import sys
input = sys.stdin.readline
from math import inf
N, M = map(int, input().split())
m_list = [0] + list(map(int, input().split()))
c_list = [0] + list(map(int, input().split()))
dp = [[0 for _ in range(sum(c_list)+1)] for _ in range(N+1)]
answer = inf
for i in range(1, N+1):
for j in range(len(dp[0])):
if c_list[i] > j:
dp[i][j] = dp[i-1][j]
else:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-c_list[i]]+m_list[i])
if dp[i][j] >= M:
answer = min(answer ,j)
print(answer)[11049] 행렬 곱셈 순서
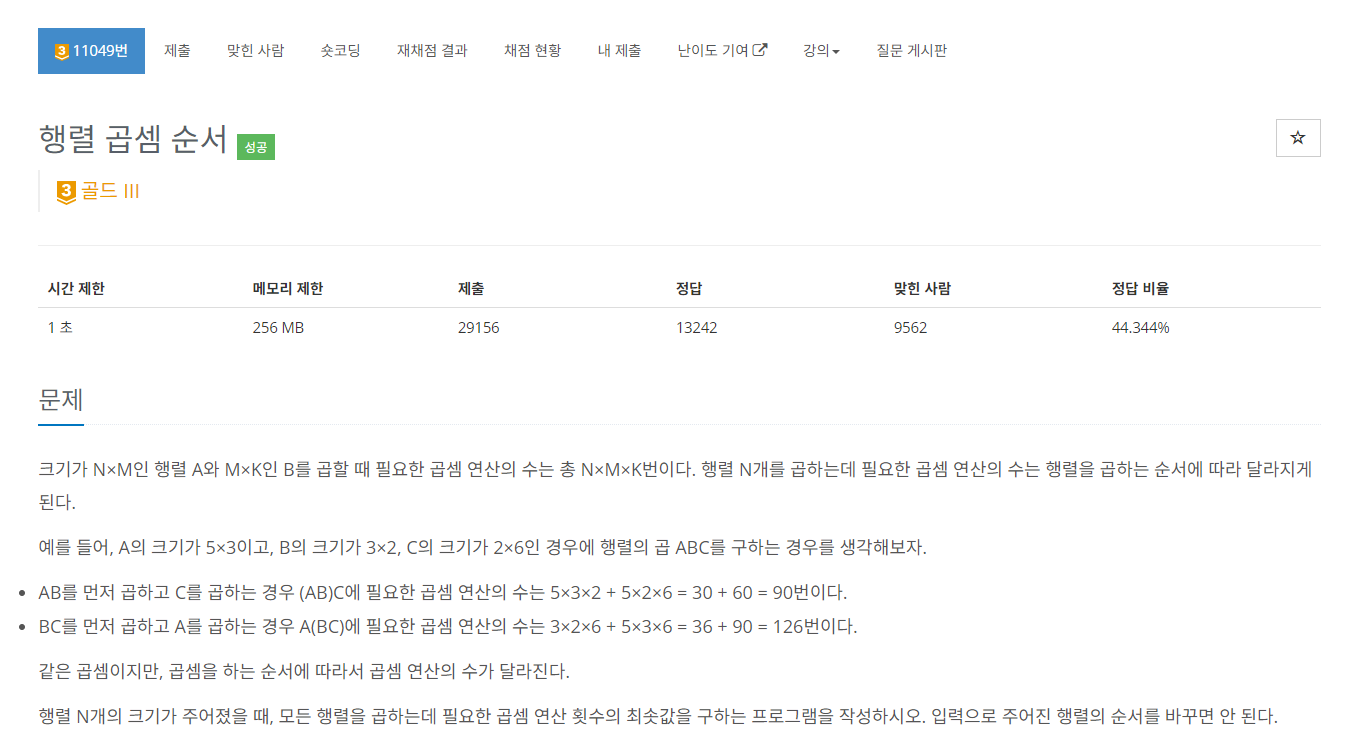
대각선으로 채우는 DP는 또 처음......
ABCDE의 곱을 계산하는 순서는 다음과 같이 쪼갤 수 있다.
- (
A) x (BCDE)- (
A) x ((B) x (CDE))- (
A) x ((B) x ((C) x (DE))) - (
A) x ((B) x ((CD) x (E)))
- (
- (
A) x ((BC) x (DE)) - (
A) x ((BCD) x (E))- (
A) x (((B) x (CD)) x (E)) - (
A) x (((BC) x (D)) x (E))
- (
- (
- (
AB) x (CDE) - (
ABC) x (DE) - (
ABCD) x (E)
행렬이 하나거나 두개의 곱까지로 쪼개야한다. 행렬 하나로는 곱을 계산할 수 없으므로 0, 행렬 두개의 곱은 무조건 MxNxK이기 때문이다.
dp가 의미하는 것은 다음과 같다.
dp[i][j] = i번째 행렬부터 j번째 행렬까지 곱할 때 최소 연산 횟수점화식 찾기
-
행렬 1개인 경우 (
i==j)=>
0으로 초기화 -
행렬 2개인 경우 (
i+1==j)=>
i번째 행렬의 행 X i번째 행렬의 열 X j번째 행렬의 열
=>matrix[i][0] * matrix[i][1] * matrix[j][1] -
행렬이 3개 이상인 경우
i <= k < j를 만족하는k에 대해서 다음과 같이 행렬의 곱을 쪼갠다.(
i번째 행렬 X ... Xk번째 행렬) X (k+1번째 행렬 X ... Xj번째 행렬)- 앞에 있는 곱
=i번째 행렬의 행 X i번째 행렬의 열 X k번째 행렬의 열
=matrix[i][0] * matrix[i][1] * matrix[k][1]
=dp[i][k] - 뒤에 있는 곱
=k+1번째 행렬의 행 X k+1번째 행렬의 열 X j번째 행렬의 열
=matrix[k+1][0] * matrix[k+1][1] * matrix[j][1]
=dp[k+1][j] - 앞에 있는 곱과 뒤에 있는 곱 합치는 비용
=i번째 행렬의 행 X k번째 행렬의 열 X j번째 행렬의 열
=matrix[i][0] * matrix[k][1] * matrix[j][1]
=> 앞에 있는 곱 + 뒤에 있는 곱 + 앞에 있는 곱과 뒤에 있는 곱 합치는 비용
=>dp[i][k] + dp[k+1][j] + matrix[i][0] * matrix[k][1] * matrix[j][1]
=> 모든k에 대해서 이 값을 구하고 가장 작은값이 최종이 된다. - 앞에 있는 곱
그리고 3번 과정에서 이전값을 제대로 가져오기 위해서는 dp배열을 대각선으로 채워야한다.

for i in range(1, N):
for j in range(N-i):
row = j # 안쪽 루프의 변수 = 행
col = j + i # 안쪽 루프의 변수 + 바깥쪽 루프의 변수 = 열코드는 다음과 같다. (위의 설명과 i/j가 반대임)
import sys
input = sys.stdin.readline
N = int(input())
matrix = []
for _ in range(N):
a, b = map(int, input().split())
matrix.append((a,b))
dp = [[0 for _ in range(N)] for _ in range(N)]
for i in range(1, N):
for j in range(N-i):
row = j
col = j + i
if i == 1:
dp[row][col] = matrix[row][0] * matrix[row][1] * matrix[col][1]
else:
dp[row][col] = 2**32
for k in range(row, col):
dp[row][col] = min(dp[row][col], dp[row][k] + dp[k+1][col] + matrix[row][0] * matrix[k][1] * matrix[col][1])
print(dp[0][-1])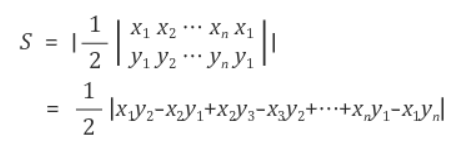

잘 보고갑니다!!