
📌 그래프는 자료구조편과 알고리즘편, 알고리즘-최단경로편, 코드편 총 4편으로 나누어서 작성
본격적으로 정리하기 전에 그래프 알고리즘에는 어떤게 있나, 하고 찾아봤더니 n년전에 학교에서 배우고 기억 저편으로 넘어갔던 알고리즘들의 어렴풋한 이름들이 우르르 나오면서 뭐가 뭔지 모르겠어서 분류를 해봤다.
- 그래프 내의 모든 정점을 순회하는 알고리즘
- DFS (완료)
- BFS (완료)
- 최소 신장 트리를 만드는 알고리즘
- 크루스칼 알고리즘
- 프림 알고리즘
- 그래프 상에서 최단경로를 탐색하는 알고리즘
- 다익스트라 알고리즘
- 벨만 포드 알고리즘
- 플로이드 워셜 알고리즘
- 작업 사이에 특정 의존(순서)관계가 있을때 이를 정렬하는 알고리즘
- 위상정렬 알고리즘
(3번 최단경로 알고리즘은 나중에 따로 주제를 빼서 작성할 예정)
우선 시작하기 전에 그래프 알고리즘에서 중요한 개념인 서로소 집합과 최소신장트리에 대해 알아보자.
1. 서로소 집합 (Disjoint Set)
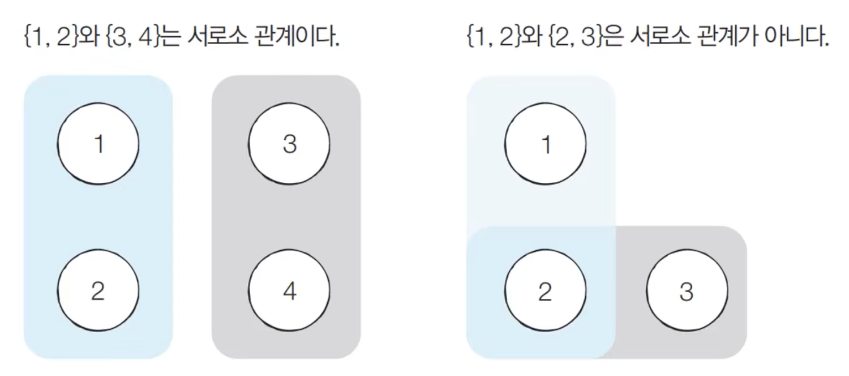
- 서로소 집합 : 공통 원소가 없는 두 집합
- 서로소 집합 자료구조 : 서로소 부분집합으로 나누어진 원소들의 데이터를 처리하기 위한 자료구조
- union(합집합) : 2개의 원소가 포함된 집합을 하나의 집합으로 합치는 연산
- find(찾기) : 특정한 원소가 속한 집합이 어떤 집합인지 알려주는 연산
(1) 합치기 연산 과정
서로소 집합 자료구조는 기본적으로 트리 자료구조를 사용한다.
union연산을 확인하고, 합치려는 두 노드A,B를 확인한다.A의 루트노드A'와B의 루트노드B'를 찾는다.A'를B'의 부모 노드로 설정한다.- 모든
union연산을 처리할 때까지 1~3번 과정을 반복한다.
cf) 부모노드를 저장하는 테이블의 초기값은 자기 자신이다.
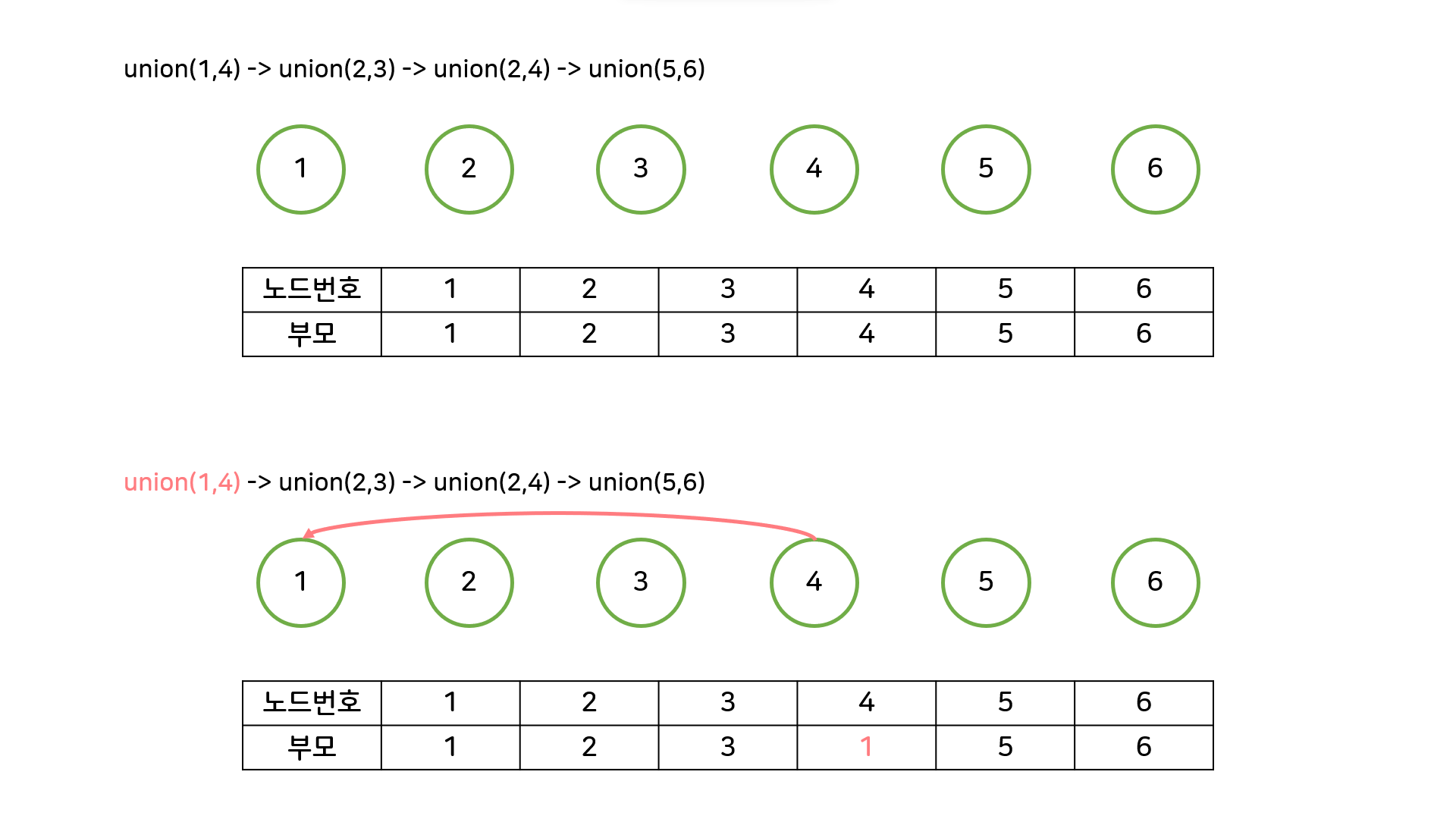

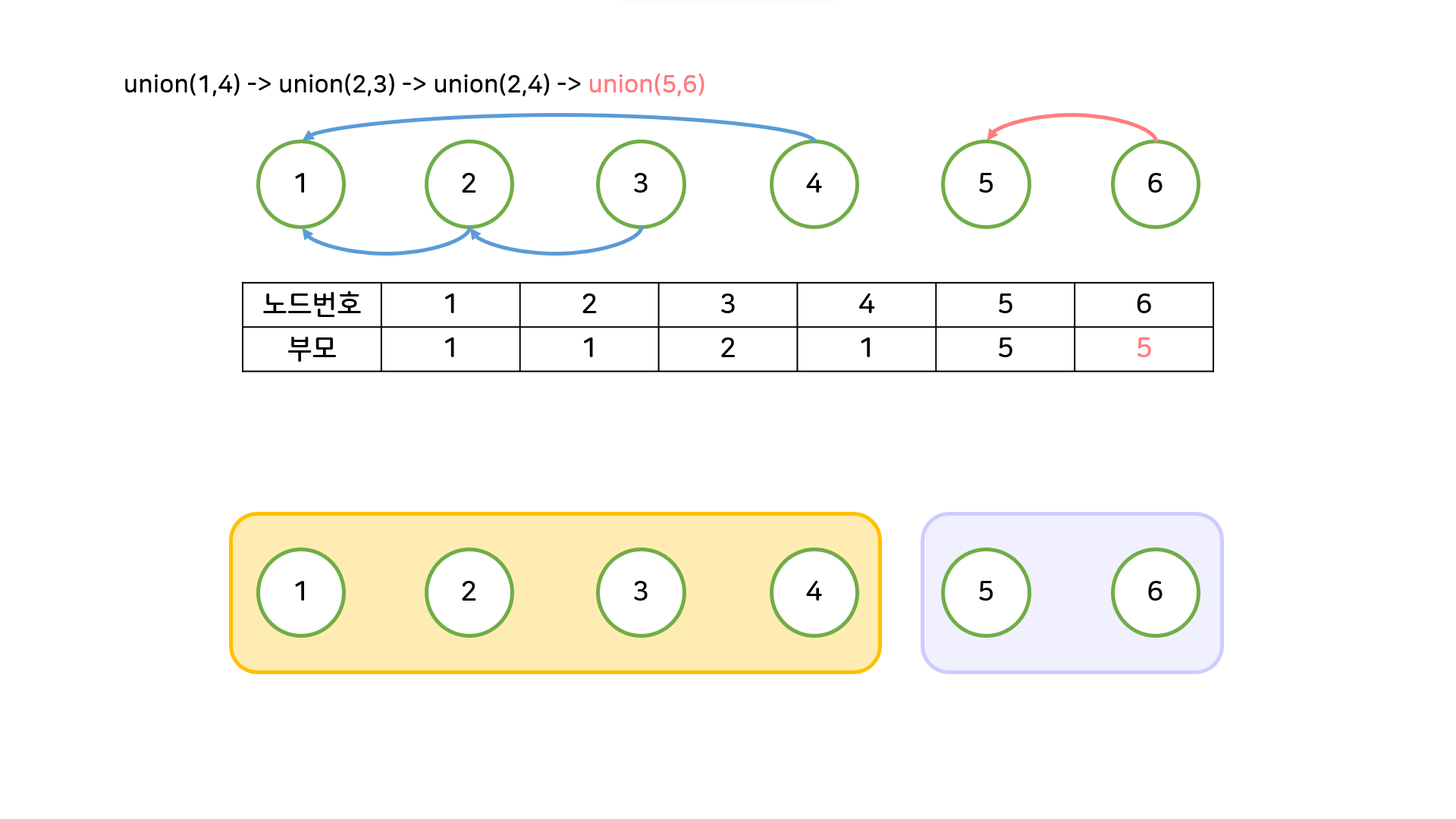
(2) union, find 구현하기
# find
def find_parent(parent, x):
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# union
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b💡 a와 b를 합칠 때 a의 부모를 b로(b의 부모를 a로) 바꾸는게 아니라, a의 부모의 부모를 b의 부모로(b의 부모의 부모를 a의 부모로) 바꾸는 것에 주의한다.
(3) 서로소 집합으로 사이클 판별하기
서로소 집합은 무방향 그래프에서 사이클을 판별할때 사용할 수 있다.
- 각 간선을 하나씩 확인하며 두 노드의 루트노드를 확인한다. (find)
- 루트노드가 서로 다르면 두 노드에 대하여 합집합 연산을 수행한다. (union)
- 루트노드가 서로 같다면 사이클이 발생한 것이다.
- 그래프에 포함되어 있는 모든 간선에 대해 1~3번 과정을 반복한다.
for e in {모든 간선} :
a, b = {간선 e에 포함된 두 노드}
if find_parent(parent, a) == find_parent(parent, b):
{사이클 발생}
break
else:
union_parent(parent, a, b)2. 최소신장트리 (MST)
(1) 신장트리 (Spanning Tree)
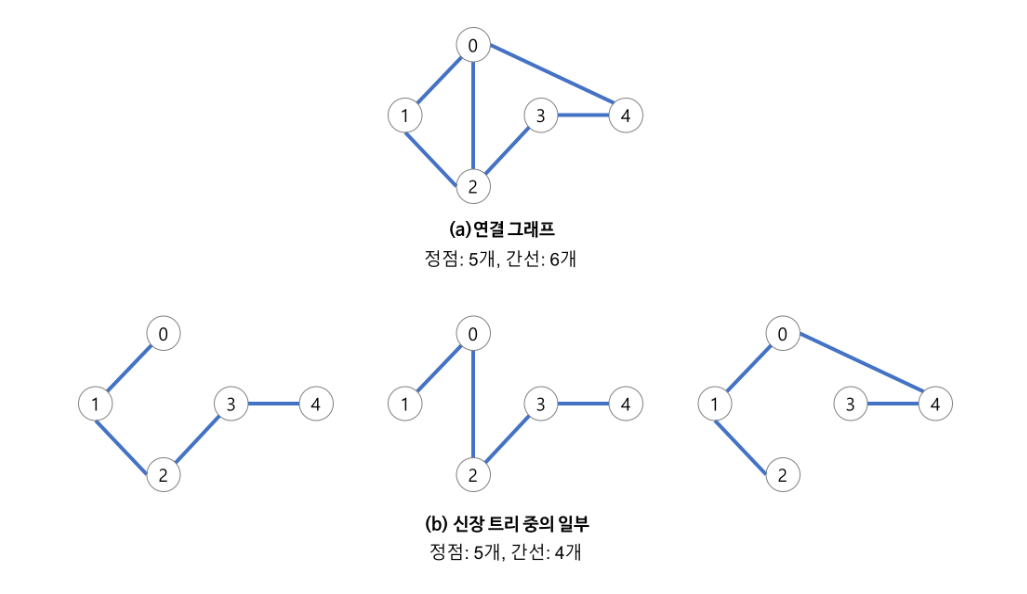
- 그래프 내의 모든 정점을 포함하는 최소 연결 부분 그래프 (간선의 수가 가장 적게, 하지만 정점은 모두 연결된 부분 그래프)
- 신장트리는 그래프에 있는 N개의 정점을 N-1개의 간선으로 연결한다.
- 하나의 그래프에 많은 신장트리가 존재할 수 있다.
- 사이클을 포함할 수 없다.
(2) 최소신장트리 (Minimum Spanning Tree)
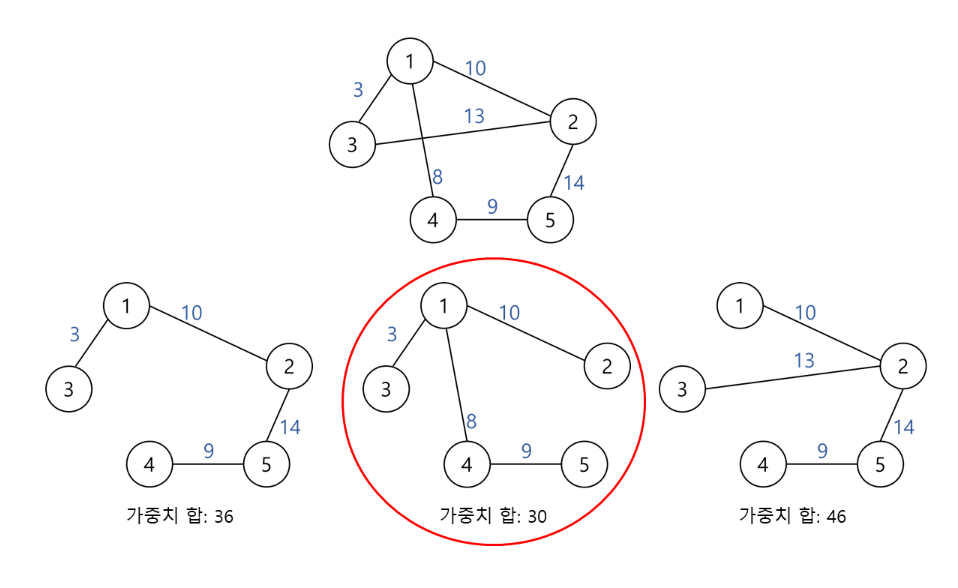
- 신장트리 중에서 사용된 간선들의 가중치 합이 최소인 트리
- 다만, 각 간선의 가중치가 동일하지 않을때 가장 적은 간선을 사용한다고 최소비용이 얻어지는 것은 아니다.
- 그럼 어떻게 구하느냐? 여기서 필요한게 바로 크루스칼 알고리즘과 프림 알고리즘이다.
3. 크루스칼 알고리즘 (Kruskal Algorithm)
(1) 동작과정
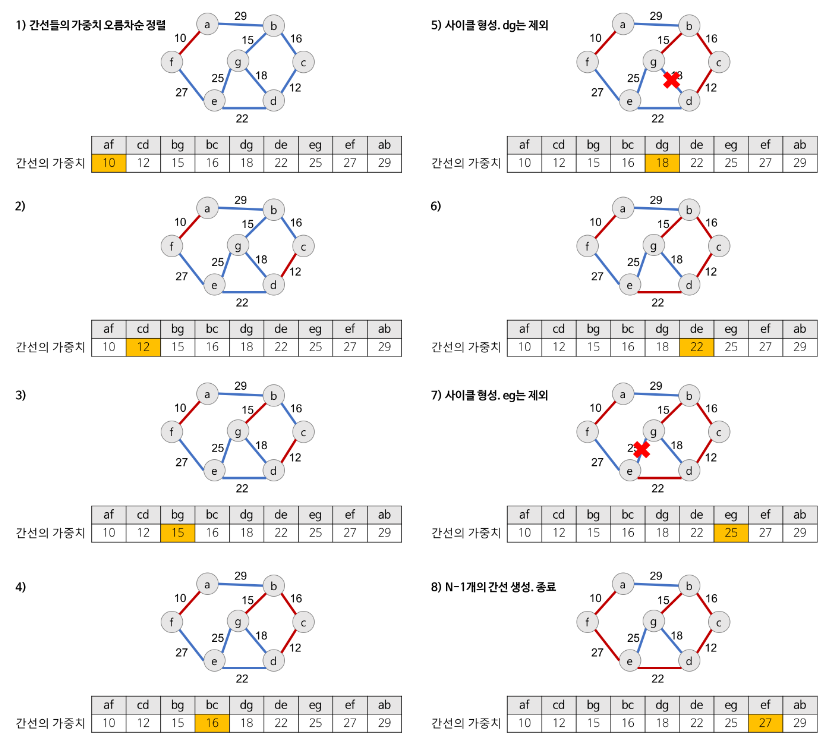
- 간선 데이터를 가중치에 따라 오름차순으로 정렬한다.
- 간선을 하나씩 확인하며 현재 간선이 사이클을 발생시키는지 확인한다.
- 사이클 발생 X -> 현재 간선을 최소신장트리에 포함시킨다.
- 사이클 발생 O -> 현재 간선을 최소신장트리에 포함시키지 않는다.
- 모든 간선에 대해서 2~4번 과정을 반복한다.
(2) 구현하기
edges = [가중치에 따라 오름차순 정렬된 모든 간선]
parent = [부모 테이블]
total_cost = 0 # 최소신장트리의 가중치
def find_parent(parent, x):
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
for i in range(간선개수):
cost, a, b = edges[i]
if find_parent(parent, a) != find_parent(parent, b):
union_parent(parent, a, b)
total_cost += cost
# 사이클이 발생하지 않았으므로 이번 edges[i]는 최소신장트리에 포함됨(3) 특징
- 모든 간선에 대해 정렬한 뒤 거리가 가장 짧은 간선부터 집합에 포함시키기 때문에 그리디 알고리즘으로 분류된다.
- 사이클 발생여부는 위에서 설명한 서로소집합의
find_parent와union_parent함수를 이용해서 확인할 수 있다. - 음수 가중치가 있을 때도 올바르게 작동한다.
4. 프림 알고리즘 (Prim Algorithm)
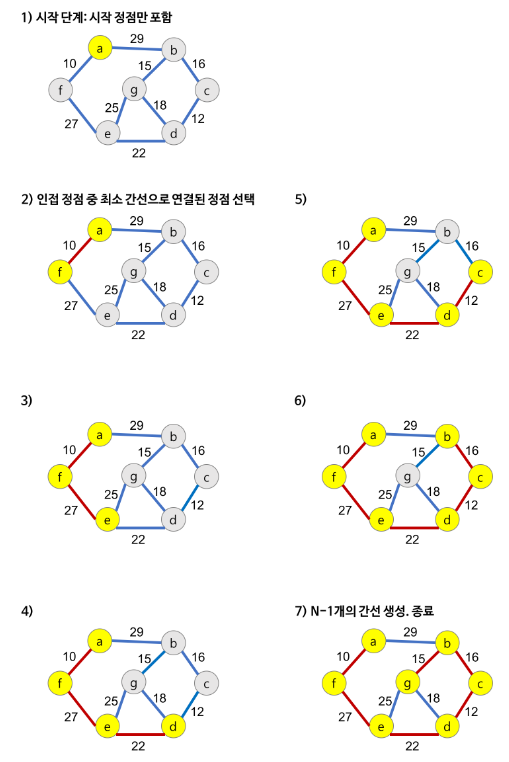
- 시작 정점을 골라서 최소신장트리에 추가한다.
- 정점과 이어진 간선을 살핀다. 간선과 이어진 다음 정점이 최소신장트리에 있지 않다면 이 정점과 간선을 최소힙에 추가한다.
- 최소힙에서 꺼낸 정점이 최소신장트리에 포함되어 있지 않다면 최소신장트리에 추가하고 2번 과정을 다시 진행한다. 만약 꺼낸 정점이 최소신장트리에 이미 포함되어있다면 그냥 넘어간다.
- 최소힙이 빌때까지 3번 과정을 반복한다.
코테에서 많이 쓰는 알고리즘은 아닌거 같아서 구현은 생략 (절대 귀찮아서 안하는거 아님)
5. 위상정렬 (Topological Sort)
(1) 개념
- 정렬 알고리즘의 일종
- 순서가 정해져 있는 일련의 작업을 차례대로 수행해야할 때 사용할 수 있는 알고리즘
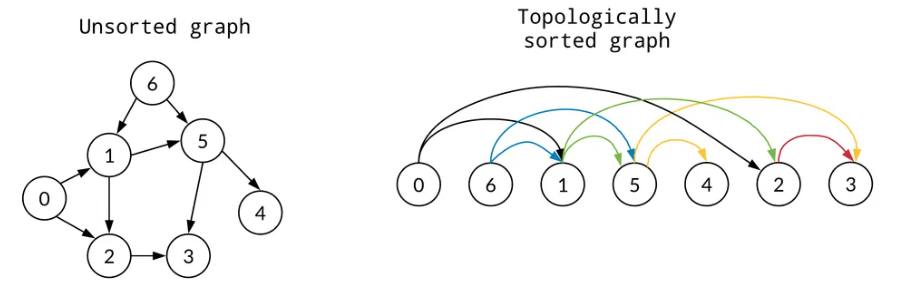
- 방향 그래프의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열하는 방법
- ex) 자료구조, 알고리즘, 운영체제 3과목이 있을때, 올바른 수강순서는 자료구조->알고리즘->운영체제이다. 자료구조->운영체제->알고리즘은 올바르지 않은 순서다.
(2) 동작과정
위상정렬은 큐를 이용하여 구현한다.
- 진입차수가 0인 노드를 큐에 넣는다.
- 큐에서 원소를 꺼내 해당 노드에서 나가는 간선을 그래프에서 제거한다.
- 새롭게 진입차수가 0이 된 노드를 큐에 삽입한다.
- 큐가 빌때까지 2~3번 과정을 반복한다.
각 노드가 큐에 들어온 순서가 위상정렬을 수행한 결과다.
(3) 구현하기
v = {노드개수}
indegree = [모든 노드에 대한 진입차수]
def topology_sort():
result = []
q = deque()
for i in range(1, v + 1):
if indegree[i] == 0:
q.append(i)
while q:
now = q.popleft()
result.append(now)
for g in graph[now]:
indegree[g] -= 1
if indegree[g] == 0:
q.append(g)
return result