
📌 그래프는 자료구조편과 알고리즘편, 알고리즘-최단경로편, 코드편 총 4편으로 나누어서 작성
1. 그래프(Graph)란?
개념
연결되어있는 원소 간의 관계를 정점(vertex/node)과 간선(edge)으로 표현한 자료구조
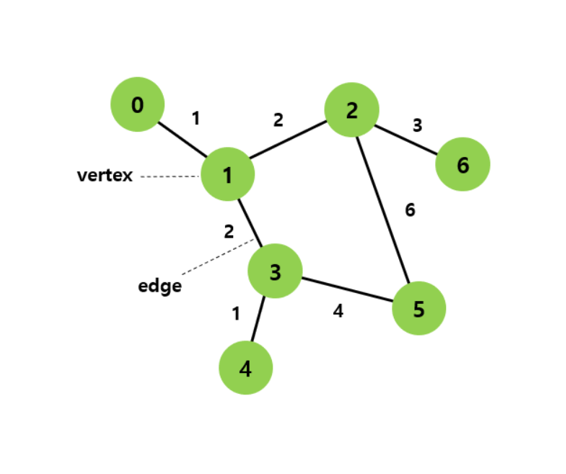
그래프는 G=(V,E)로 표현한다.
V= 정점의 집합E= 간선의 집합
용어
기본
- 정점(vertex/node) : 데이터를 저장하는 위치
- 간선(edge/link/branch) : 정점들을 연결하는 선
정점
- 인접(adjacent) : 무방향 그래프에서 정점 A, B 사이에 간선이 존재한다면 정점 A는 정점 B에 인접한다.
- 인접 정점(adjacent vertex) : 간선에 의해 직접 연결된 정점
- 차수(degree) : 무방향 그래프에서 하나의 정점에 인접한 정점의 수
간선
- 부속(incident) : 무방향 그래프에서 정점 A, B 사이에 간선이 존재한다면 간선 (A, B)는 정점 A, B에 부속한다.
- 진입 차수(in-degree) : 방향 그래프에서 외부에서 들어오는 간선의 수
- 진출 차수(out-degree) : 방향 그래프에서 외부로 향하는 간선의 수
경로(path)
- 경로(path) : 간선을 통해 정점들을 지나다니면서 생기는 경로 (이미 사용된 간선과 정점은 다시 사용하지 않는다.)
- 경로 길이(path length) : 경로를 구성하는데 사용된 간선의 수
- 단순 경로(simple path) : 반복되는 정점이 없는 경로
- 순환(cycle) : 단순 경로의 시작 정점과 종료 정점이 동일한 경우 (<-> 반대 : 비순환(acyclic))
- 셀프루프/루프(self-loop/loop) : 정점에서 진출한 간선이 다른 정점을 거치지 않고 곧바로 자기 자신에게 진입하는 경우
📍 순환 : 3 -> 2 -> 1 -> 3
📍 루프 : 3 -> 3
경로 번외편
- 경로(trail) : 같은 간선이 두 번 이상 반복되지 않는 경로 (정점은 반복 가능)
- 회로(circuit) : 출발점과 도착점이 같은 경로(trail)
💡 path, circuit, cycle은 trail의 특수한 케이스
= circuit은 trail의 특수한 케이스 + cycle은 path의 특수한 케이스
🔸trail : 간선 반복 X, 정점 반복 O
🔸circuit : 간선 반복 X, 정점 반복 O, 시작 정점 = 마지막 정점
🔹path : 간선 반복 X, 정점 반복 X
🔹cycle : 간선 반복 X, 정점 반복 X, 시작 정점 = 마지막 정점 - 오일러경로 : 그래프에 존재하는 모든 간선을 한번만 통과해서 처음 정점으로 돌아오는 경로 (그래프의 간선이 짝수개일때만 존재한다.)
특징
- 그래프는 순환 또는 비순환 구조를 이룬다.
- 방향이 있는 그래프와 방향이 없는 그래프가 있다.
- 루트노드, 부모-자식 관계라는 개념이 없다.
- 두 정점 사이에서 양방향 경로를 가질 수 있다.
- self-loop/loop/circuit 모두 가능하다.
- 순회는 DFS나 BFS로 이루어진다.
- 간선의 유무는 그래프에 따라 다르다. (정점마다 간선이 존재하지 않을 수도 있다.)
- 그래프는 네트워크 모델이다.
종류
- 무방향 그래프 vs 방향 그래프
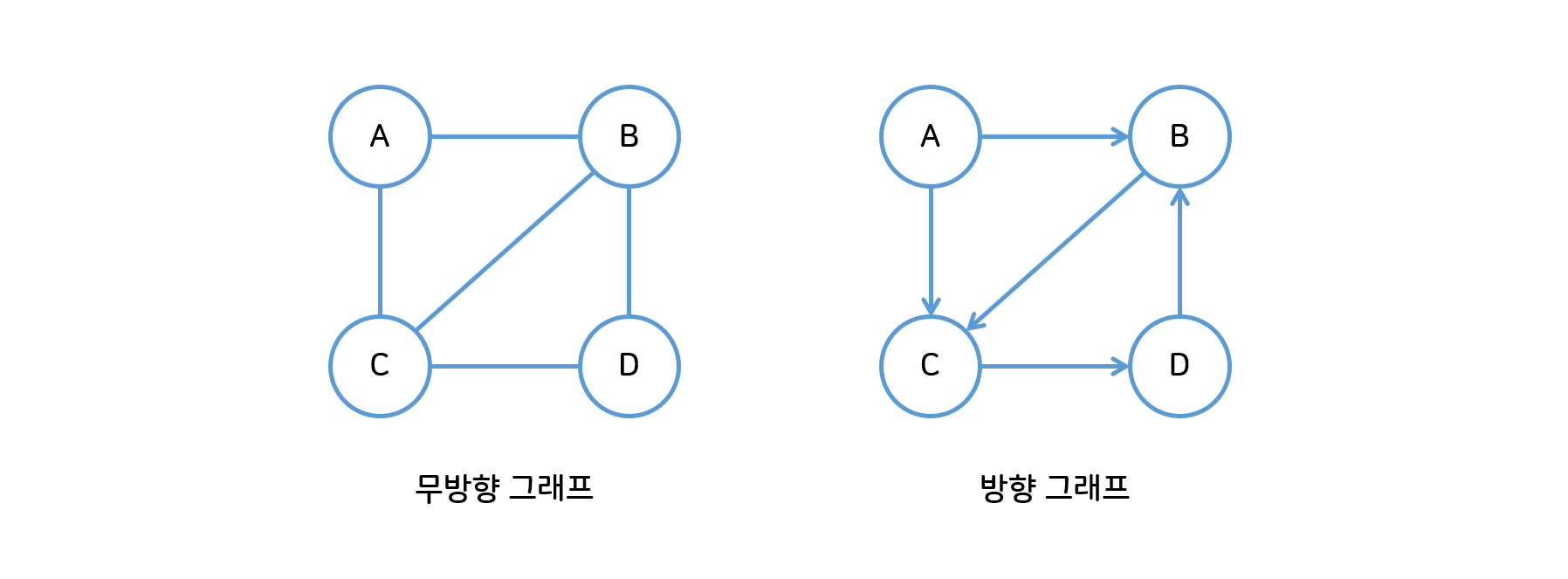
- 무방향 그래프(Undirected Graph) : 두 정점을 연결하는 간선에 방향이 없는 그래프
- 방향 그래프(Directed Graph) : 두 정점을 연결하는 간선에 방향이 있는 그래프
- 연결 그래프 vs 비연결 그래프
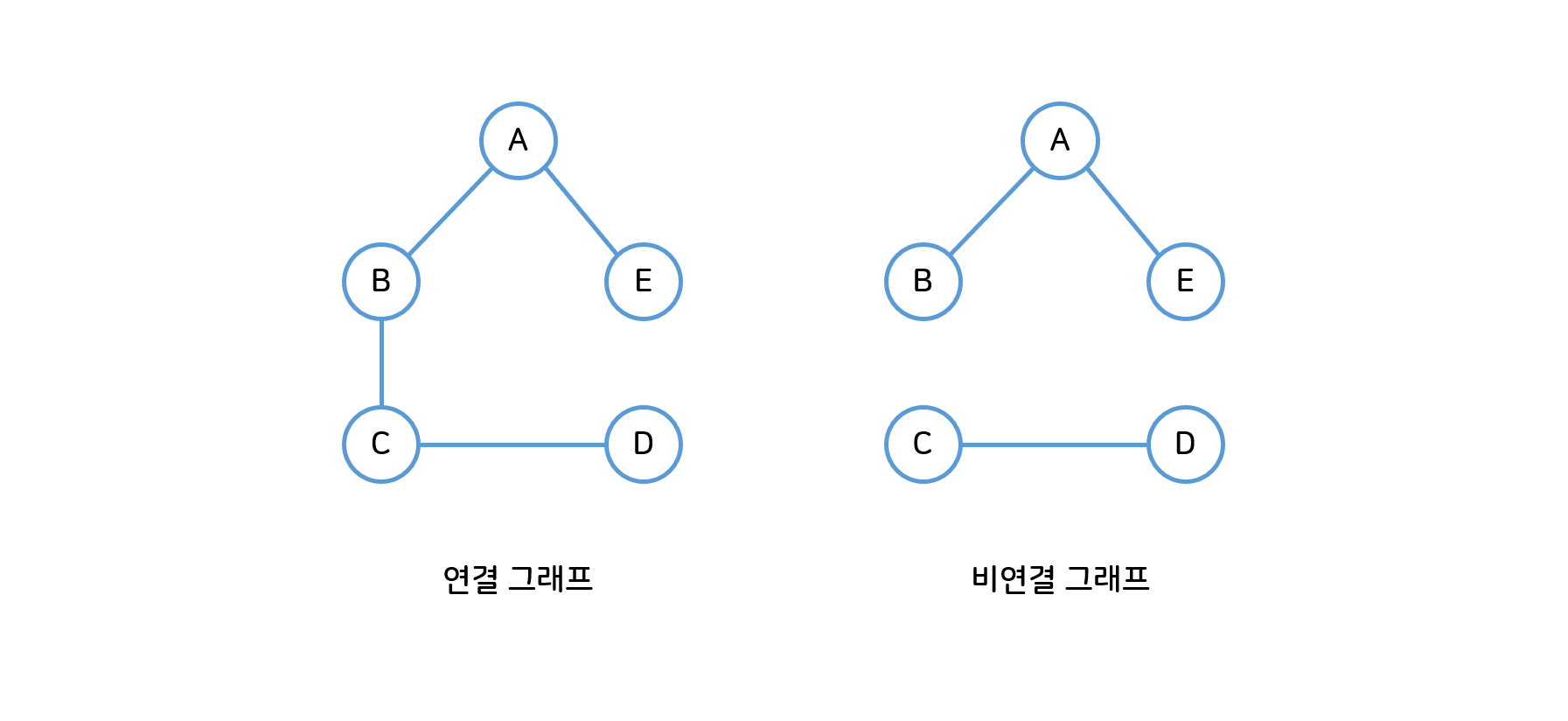
- 연결 그래프(Connected Graph) : 떨어져있는 정점이 없는 그래프
- 비연결 그래프(Disconnected Graph) : 연결되지 않은 정점이 있는 그래프
- 완전 그래프
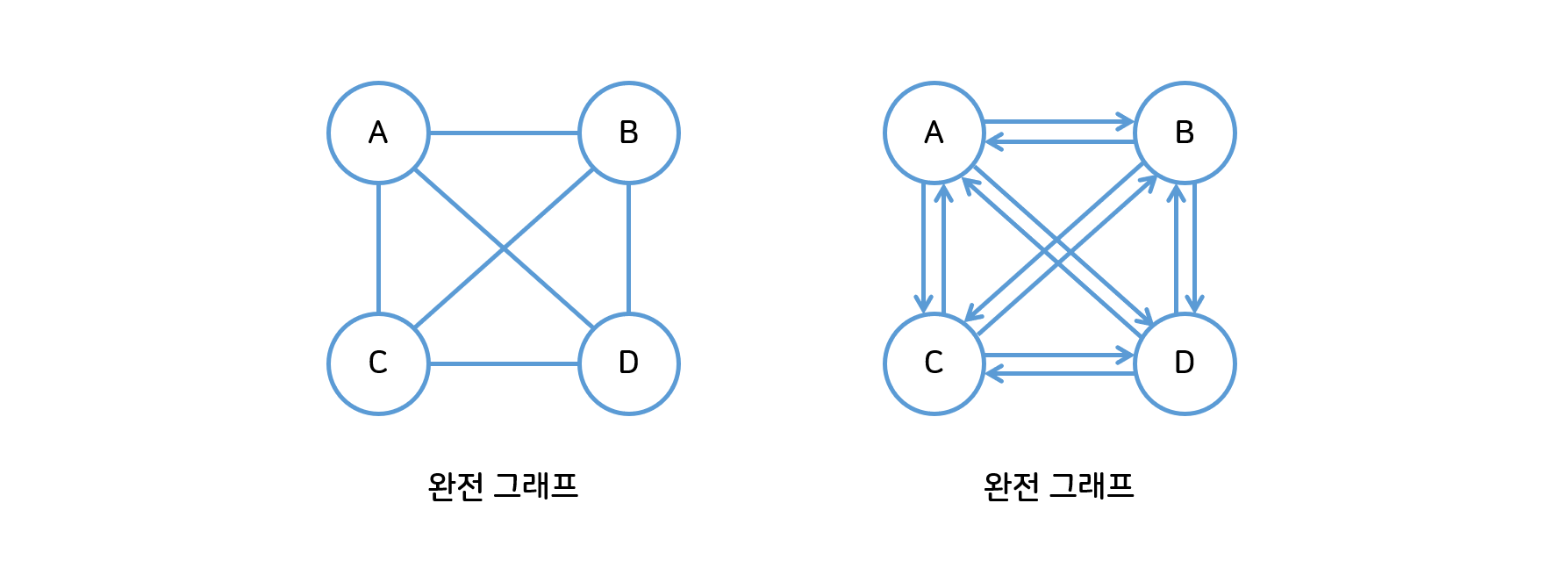
- 완전 그래프(Complete Graph) : 각 정점에서 다른 모든 정점이 연결된, 최대한 많은 간선 수를 가진 그래프
- 정점이 N개인 무방향 그래프에서 최대 간선 수 = N(N-1)/2 개
- 정점이 N개인 방향 그래프에서 최대 간선 수 = N(N-1)개
- 부분 그래프
- 부분 그래프(Subgraph) : 원래 그래프에서 일부 정점이나 간선을 제외하고 만든 그래프
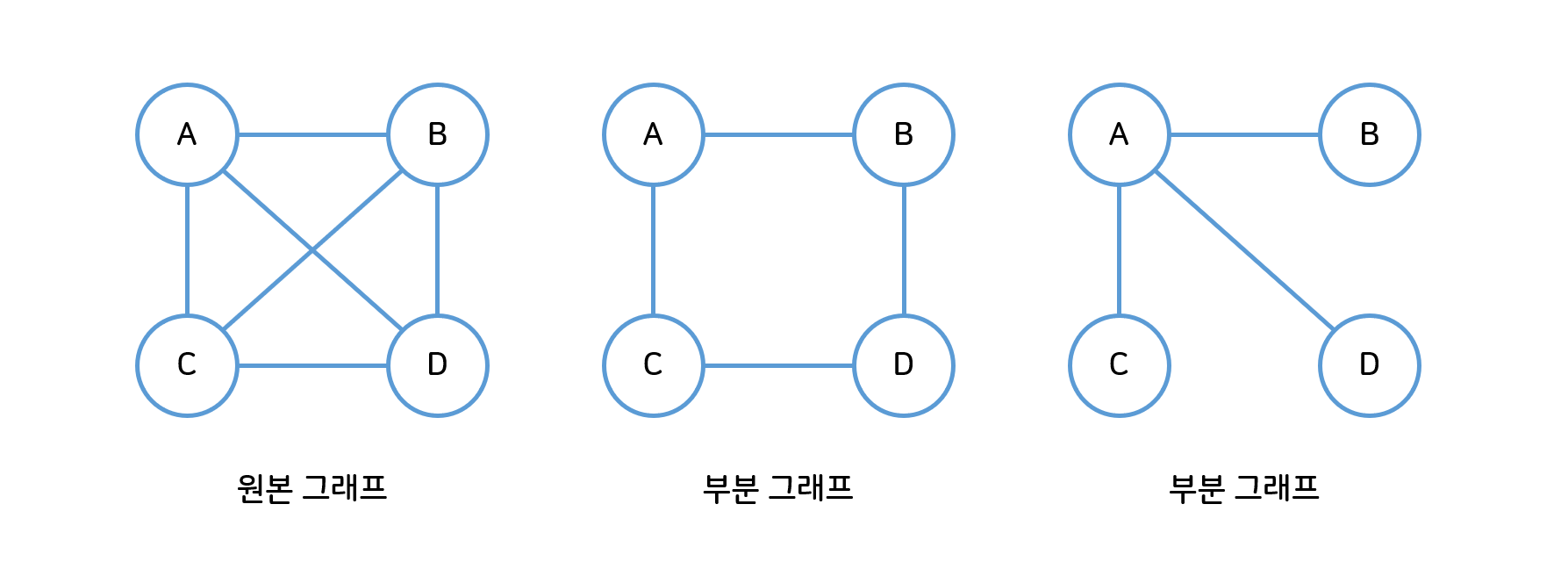
- 가중치 그래프
- 가중치 그래프(Weighted Graph) : 간선에 가중치가 부여되어 있는 그래프
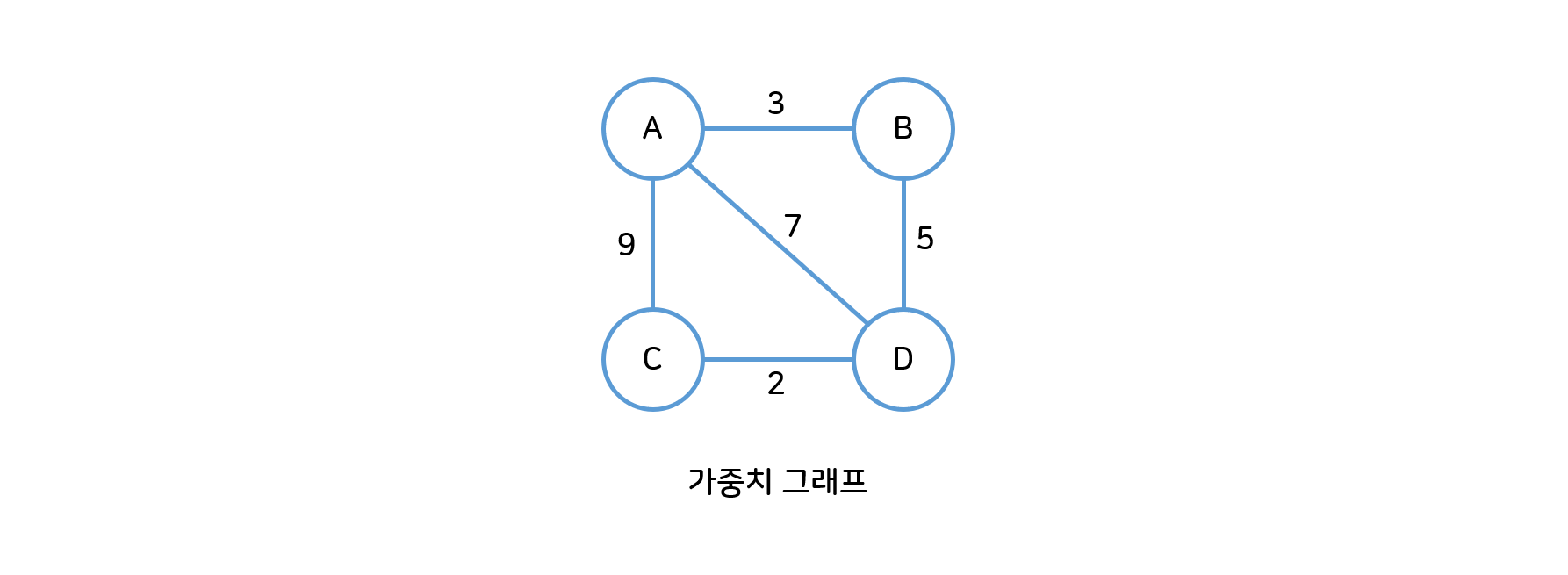
- 순환 그래프(사이클) vs 비순환 그래프
- 순환 그래프(Cyclic Graph) : 단순 경로의 시작 정점과 종료 정점이 동일한 그래프 (사이클이 있는 그래프)
- 비순환 그래프(Acyclic Graph) : 사이클이 없는 그래프
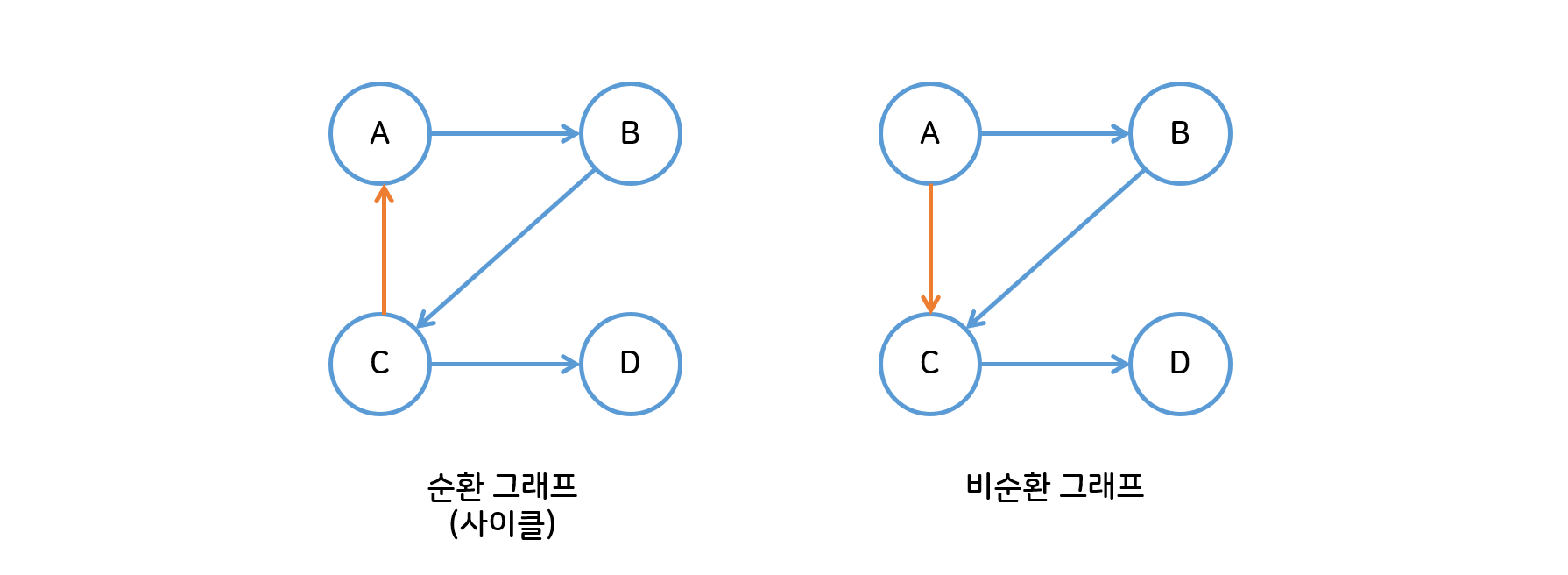
구현
탐색
2. 트리(Tree)란?
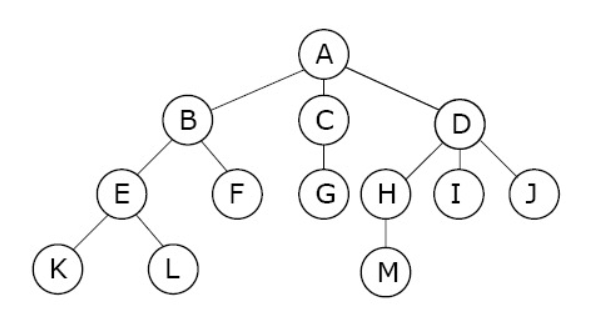
개념과 특징
- 노드(node)들과 노드들을 연결하는 간선(edge)으로 이루어진 자료구조
- 한 개의 루트노드만이 존재하고, 모든 자식노드는 한 개의 부모노드만을 가진다.
- 그래프의 일종으로, 사이클이 없는 하나의 연결 그래프(Connected Graph)이거나 방향성이 있는 비순환 그래프(Directed Acyclic Graph)의 한 종류이다.
- 사이클이 존재할 수 없다. self-loop/loop/circuit 모두 불가능하다.
- 노드가 N개인 트리는 항상 N-1개의 간선을 가진다.
- 임의의 두 노드 간의 경로는 유일하다. 두 정점 사이에 반드시 1개의 경로만을 가진다.
- '최소 연결 트리'라고도 불린다.
- 계층모델이다.
- 순회는 pre-order, in-order, post-order로 이루어진다.
용어
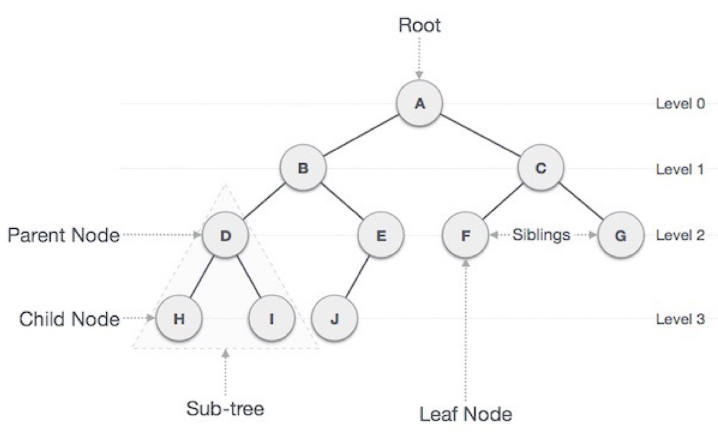
트리의 구성요소
- 노드(node) : 트리를 구성하는 각각의 요소
- 간선(edge) : 트리를 구성하기 위해 노드와 노드를 연결하는 선
- 루트노드(root node) : 트리 구조에서 최상위에 있는 노드
- 부모노드(parent node) : 자식노드를 가진 노드
- 자식노드(child node) : 부모노드를 가진 노드
- 형제노드(sibling node) : 같은 부모를 가지는 노드
- 단말노드(leaf node) : 자식노드가 없는 노드
- 비단말노드(internal node) : 자식노드가 있는 노드
트리의 특징/속성
- 깊이(depth) : 루트노드에서 어떤 노드에 도달하기 위해 거쳐야 하는 가장 긴 경로의 간선의 수
- 높이(height) : 루트노드에서 가장 깊숙히 있는 노드의 깊이
- 레벨(level) : 루트노드에서 임의의 노드까지의 깊이 (루트노드의 레벨=1)
- 차수(degree) : 노드의 자식 수
- 크기(size) : 자신을 포함한 자손노드의 수
- (width) : 해당 레벨에 있는 노드의 수
- (breadth) : 단말노드의 수
종류
트리에는 여러 종류가 있는데, 그 중 이진트리가 가장 기본이 되는 형태다.
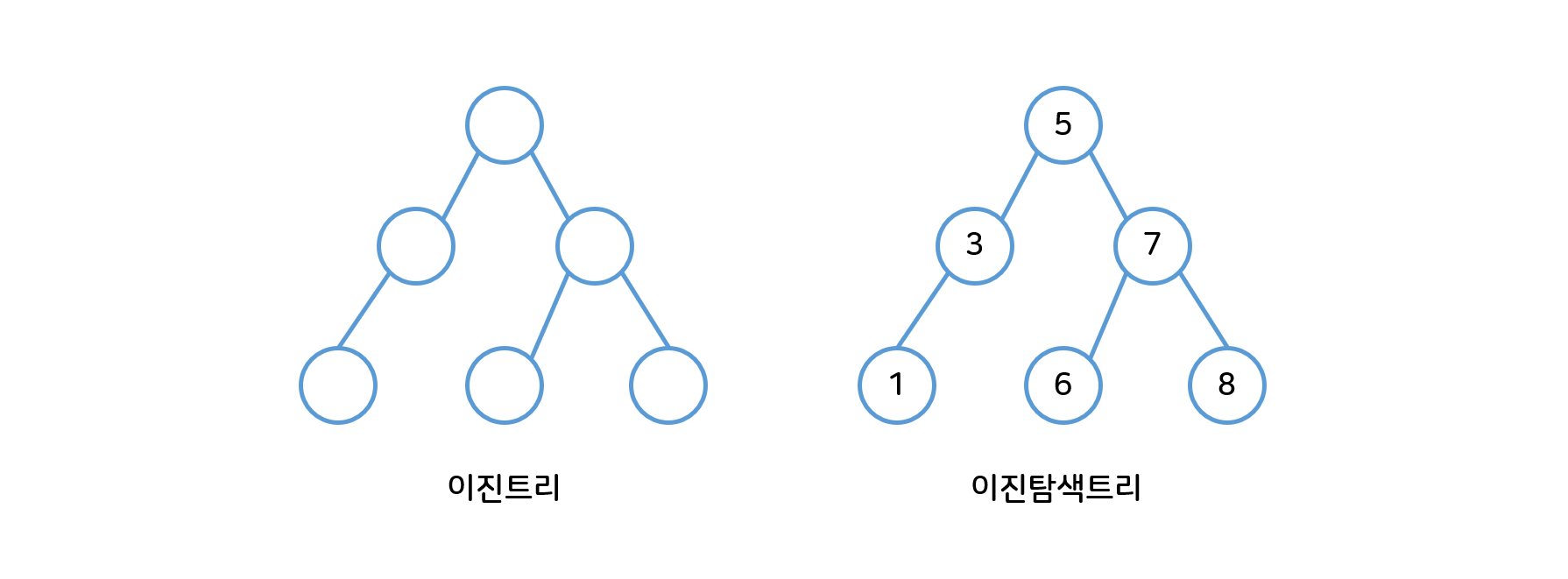
- 이진트리 vs 이진탐색트리
- 이진트리(Binary Tree) : 각 노드가 최대 2개의 자식을 갖는 트리 (0개, 1개도 가능)
- 이진탐색트리(Binary Search Tree) : 모든 노드에 대해서 왼쪽 자식노드에는 부모노드보다 작은 값이, 오른쪽 자식노드에는 부모노드보다 큰 값이 들어가있어야 하는 이진트리
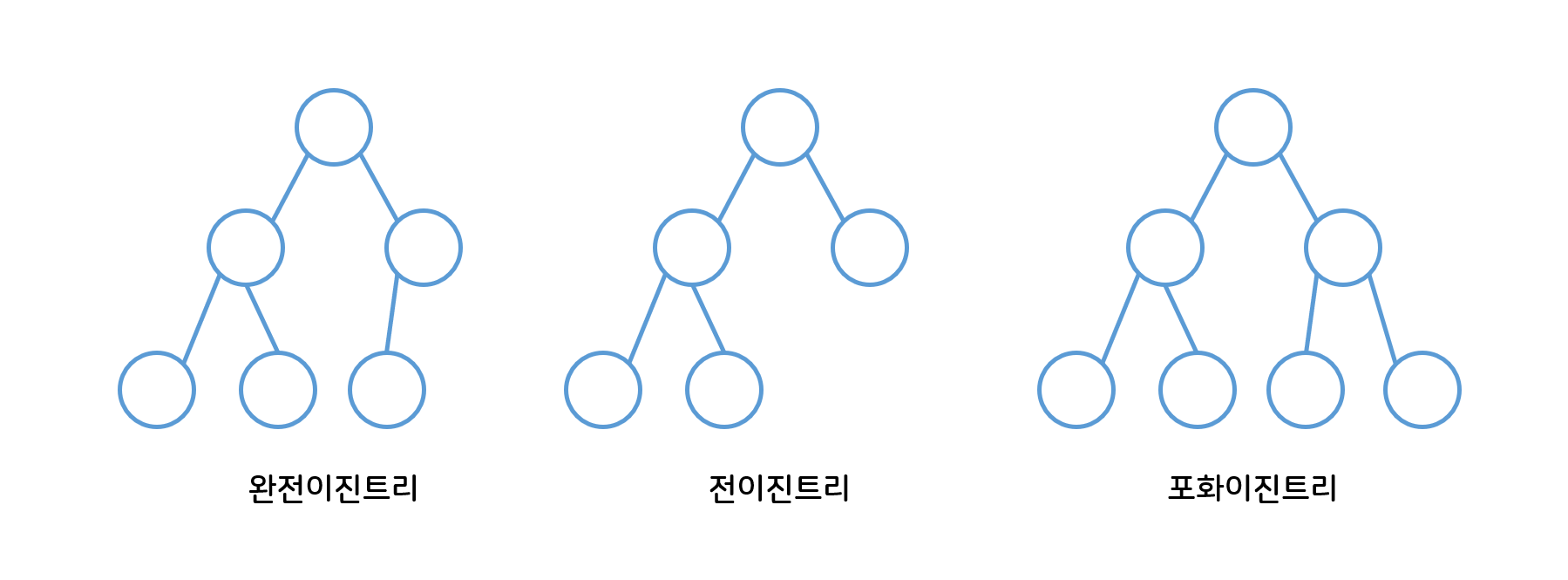
- 완전이진트리 vs 전이진트리 vs 포화이진트리
- 완전이진트리(Complete Binary Tree) : 왼쪽에서 오른쪽으로 순서대로 모두 차곡차곡 채워져있는 이진트리
- 전이진트리(Full Binary Tree) : 모든 노드가 0개 또는 2개의 자식노드를 가지는 이진트리
- 포화이진트리(Perfect Binary Tree) : 단말노드를 제외한 모든 노드의 차수가 2개로 이루어져 있는 경우 (전이진트리이면서 완전이진트리인 트리)
- 이진힙
- 신장트리
트리 순회
➕ 2023-08-10 추가
전엔 그냥 넘어갔었는데 백준 문제를 풀다가 트리 순회 문제가 있어서 정리
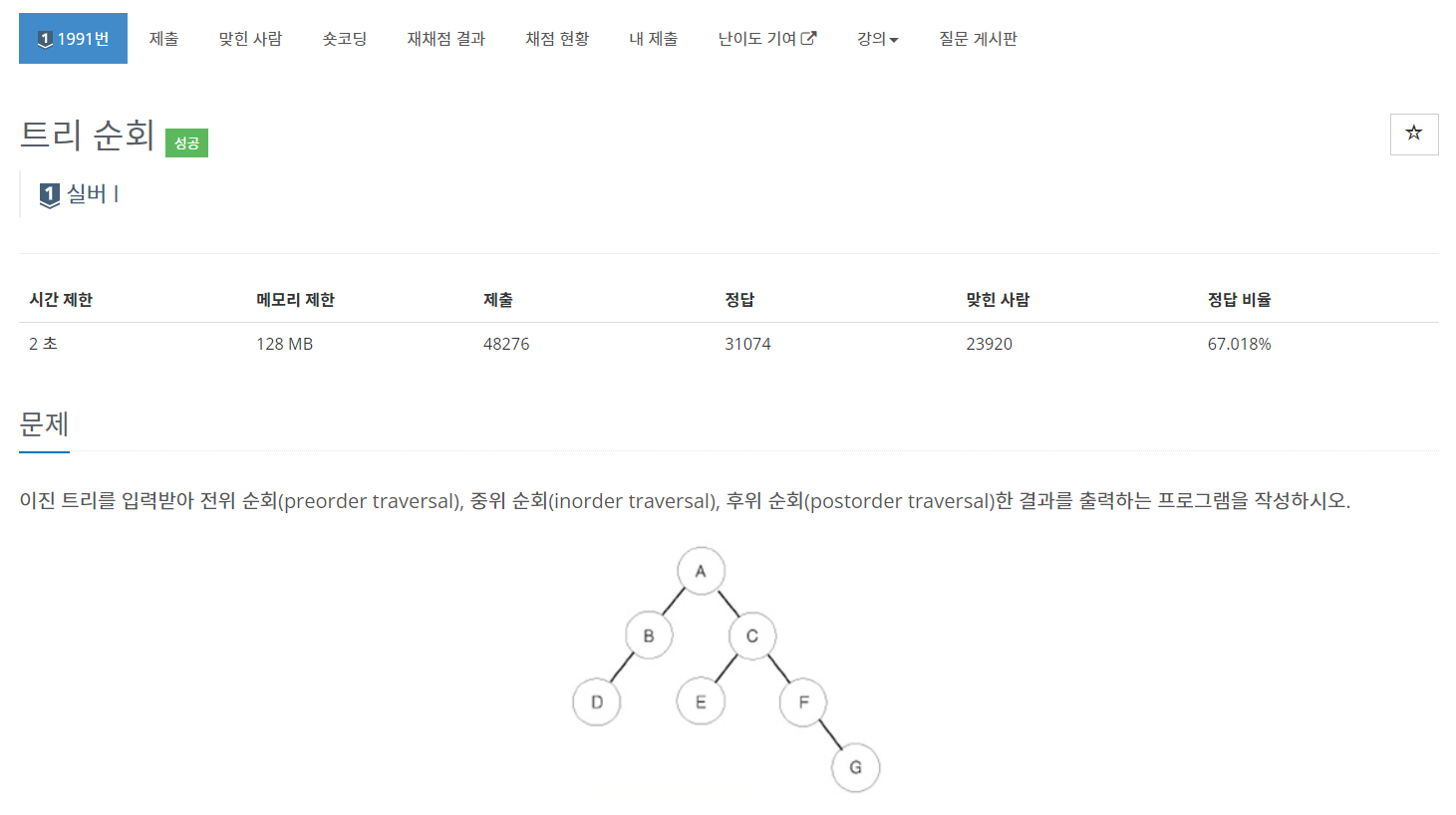
이후에 작성할 순회 함수들을 호출하는 메인함수는 다음과 같다.
def main():
N = int(input())
tree = dict()
for _ in range(N):
node, left, right = input().split()
tree[node] = (left, right)
preorder(tree, 'A')
print()
inorder(tree, 'A')
print()
postorder(tree, 'A')
print()❗ 순회 방법과 상관없이 시작노드는 항상 루트노드이다. (중위, 후위에서는 당장 방문하지 않을 뿐)
(1) 전위 순회 (preorder)
루트 -> 왼쪽 자식 -> 오른쪽 자식

A -> B -> D -> C -> E -> F -> G
def preorder(tree, node):
if node != '.':
print(node, end='') # 루트
preorder(tree, tree[node][0]) # 왼쪽 자식
preorder(tree, tree[node][1]) # 오른쪽 자식
return(2) 중위 순회 (inorder)
왼쪽 자식 -> 루트 -> 오른쪽 자식
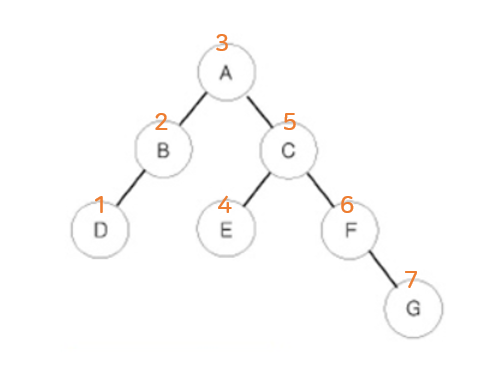
D -> B -> A -> E -> C -> F -> G
def inorder(tree, node):
if node != '.':
inorder(tree, tree[node][0]) # 왼쪽 자식
print(node, end='') # 루트
inorder(tree, tree[node][1]) # 오른쪽 자식
return(3) 후위 순회 (postorder)
왼쪽 자식 -> 오른쪽 자식 -> 루트
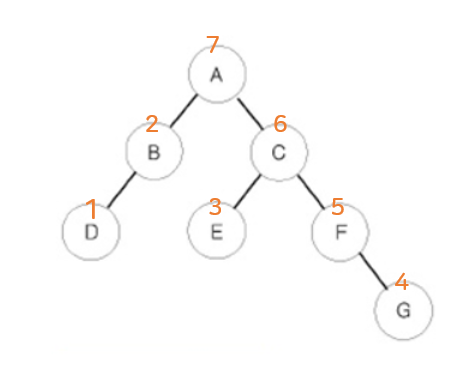
D -> B -> E -> G -> F -> C -> A
def postorder(tree, node):
if node != '.':
postorder(tree, tree[node][0]) # 왼쪽 자식
postorder(tree, tree[node][1]) # 오른쪽 자식
print(node, end='') # 루트
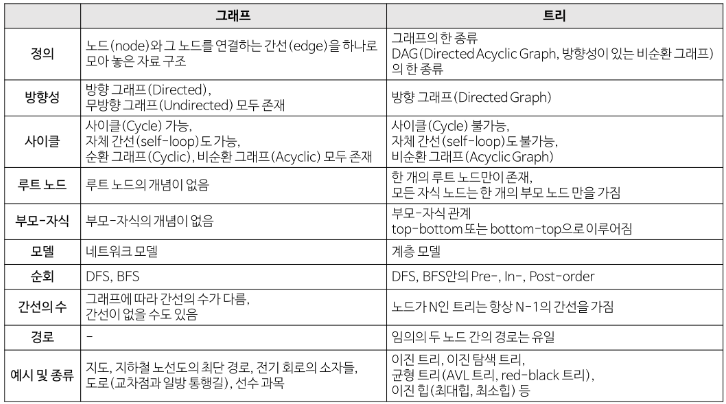
return3. 그래프 vs 트리

좋은 정보 감사합니다