
📌 "무식해 보여도 사실은 최고의 방법일 때가 있지요. 가능한 모든 상황을 조사해 문제를 풀어보세요."
출제빈도 : 높음
평균점수 : 낮음
완전탐색(Brute Force)이란?
무식하게 모든 경우를 탐색해보는 알고리즘
정확성은 100% 보장되나 속도가 최악이다.
문제에서 주어진 데이터가 매우 적을때만 사용 가능하다.
완전탐색은 딱히 알고리즘이라고 할게 없지만, 완전탐색을 하기 위한 기법들은 여러개가 있다.
1. 단순 브루트포스
for문과 if문 등으로 모든 케이스를 조사해보는 방법
코테에 단독으로는 거의 나오지 않는다.
2. 순열
서로 다른 n개 중 r개를 중복없이 선택하여 나열하는 경우의 수
순서 상관 O, [1, 2, 3]과 [3, 2, 1]은 다른 것
완전탐색의 대표적인 유형이다.
- 순열
>>> from itertools import permutations
>>> list(permutations([1,2,3], 2))
[(1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2)]- 조합
>>> from itertools import combinations
>>> list(combinations([1,2,3], 2))
[(1, 2), (1, 3), (2, 3)]- 중복순열
>>> from itertools import product
>>> list(product([1,2,3], repeat=2))
[(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)]- 중복조합
>>> from itertools import combinations_with_replacement
>>> list(combinations_with_replacement([1,2,3], 2))
[(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3)]3. 재귀
자기 자신을 호출한다는 의미
자신이 수행할 작업을 유사한 형태의 여러 조각으로 쪼갠 뒤 그 중 한 조각을 수행하고, 나머지는 자기 자신을 호출해 실행한다.
반복문을 줄일 수 있지만, 스택 오버플로우가 잘 발생해서 조심해서 써야 한다.
현재 함수의 상태를 저장하는 파라미터와 재귀 탈출 조건이 반드시 필요하고, return 문을 명확하게 정의해야 한다.
ex. 간단한 재귀함수 예시 (팩토리얼)
def recursive_factorial(n):
if n <= 1:
return 1
return n * recursive_factorial(n-1)
print(recursive_factorial(5))120재귀함수는 BFS/DFS에서 주로 사용된다.
4. 비트마스크
2진수를 사용하여 연산하는 방식
각 원소가 포함 or 불포함으로 구성되는 경우에 사용된다.
ex. [1, 2, 3, 4]의 부분집합을 만들때, 비트마스크를 사용하면
[1, 2, 3, 4]
1 1 1 1
1 1 1 0
1 1 0 1
1 1 0 0
...리스트의 길이 만큼 비트 리스트를 만든 후에 원소가 포함되면 1, 아니면 0으로 구분해서 간단하게 표기할 수 있다.
비트연산(&, |, ^, ~, <<, >>)이 가능하다.
➕ 2023-07-29 추가
[코테, 알고리즘] 백준 class 3 - 비트마스크
5. BFS/DFS
나중에 따로 빼서 쓸거라서 이번에는 패스
➕ 2023-07-22 추가
[코테, 알고리즘] 프로그래머스 고득점 Kit - DFS/BFS (1)
6. 백트래킹
해를 찾는 도중에 막히면 더 이상 깊이 들어가지 않고, 이전 단계로 되돌아가서 해를 찾아나가는 기법
불필요한 부분을 쳐내고(가지치기) 최대한 올바른 방향으로 나아가려는 방식
백트래킹을 사용하는 대표적인 알고리즘이 DFS인데, DFS는 재귀를 통해 가능한 경로 중 유망한 경로만 찾아서 탐색을 수행한 뒤 다시 돌아와 그 중 가장 최적의 경로를 반환하는 것이다.
완전탐색 시간복잡도
비트마스크 > DFS/BFS > Brute-Force > 재귀함수 > 순열 > 백트래킹
코드
1. 소수찾기 (Lv. 2)
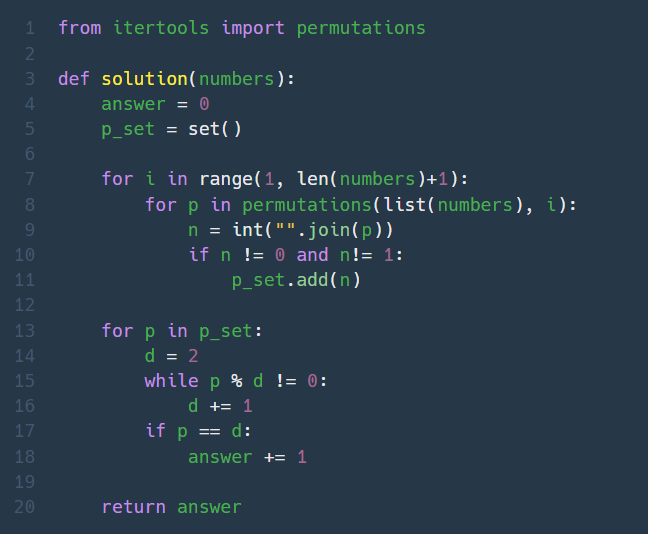
소수 판별을 에라토스테네스의 체로 구하려고 했는데, 순열로 조합한 모든 수들이 그렇게 많지 않아서 오히려 비효율적일 것 같아 그냥 일일이 확인했다.
2. 카펫 (Lv. 2)
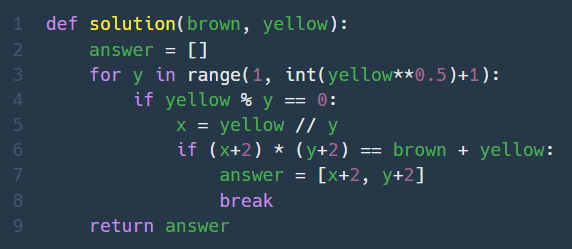
yellow를 가능한 모든 약수의 곱으로 나눠 표현한 다음에, 두 약수에 2씩 더한 수끼리의 곱이 brown+yellow와 같다는 조건에 걸리면 답 반환
3. 피로도 (Lv. 2)
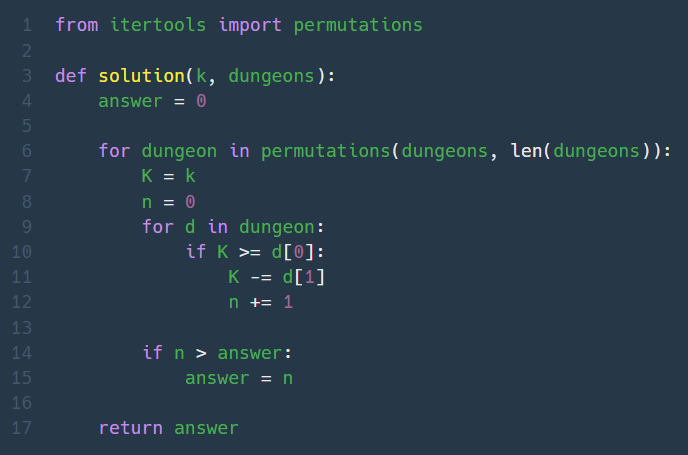
던전 방문 순서를 '(필요 피로도-소모 피로도) 내림차순 & 소모 피로도 오름차순'으로 정렬해서 순서대로 방문하게 하려고 했는데, 규칙찾기 반례에 실패해서 던전들의 모든 방문순서를 순열로 구해 그중 최대값을 찾았다.
4. 전력망을 둘로 나누기 (Lv. 2)

끊을 수 있는 전선의 모든 경우의 수마다 집합을 이용해 몇개씩 이어져 있는지 세는 로직은 맞았는데 테케 몇개에서 계속 실패하다가 for _ in left_wires 한줄 추가로 통과됐다. 한번만 돌아서는 이어져있는 모든 송전탑을 알 수 없기 때문에 한번 더 돌아줘야했는데 안했다.
5. 모음사전 (Lv. 2)
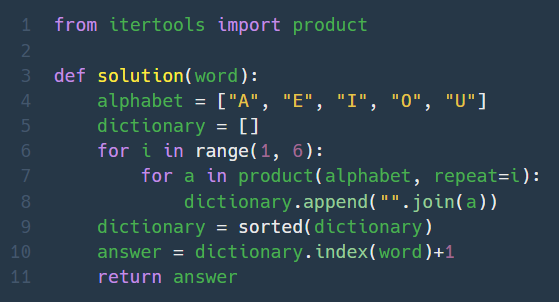
가능한 모든 경우의 수를 모두 구해서 아예 사전을 만든 다음에 인덱스를 찾았다.
느낀점
- 공통적으로 문제에서 가능한 모든 경우의 수를 다 고려해봐야 통과할 수 있었다.
- 그 모든 가능한 경우의 수를 주로 '순열'로 구한다는 점에서, 순열이 완전탐색의 대표적인 유형이라는게 무슨말인지 알 것 같았다.
- BFS/DFS, 재귀, 백트래킹은 완전탐색이긴 한데 뭔가 결이 다른거 같아서 이번 풀이에선 안썼다. 다음에 BFS/DFS 키트 풀면서 더 정리해봐야겠다.
