
📌 "정렬을 이용해서 문제를 효율적으로 풀어보세요."
출제빈도 : 높음
평균점수 : 높음
정렬이란?
데이터를 특정한 기준에 따라 순서대로 나열하는 것
여러가지 정렬 알고리즘이 있지만 이번에는 대표적인 정렬 알고리즘인 선택정렬, 삽입정렬, 퀵정렬, 계수정렬, 버블정렬, 합병정렬에 대해 알아보도록 하겠다.
1. 선택정렬 (Selection Sort)
처리되지 않은 데이터 중에서 가장 작은 데이터를 선택해 맨 앞에 있는 데이터와 바꾸는 것을 반복하여 정렬하는 방법
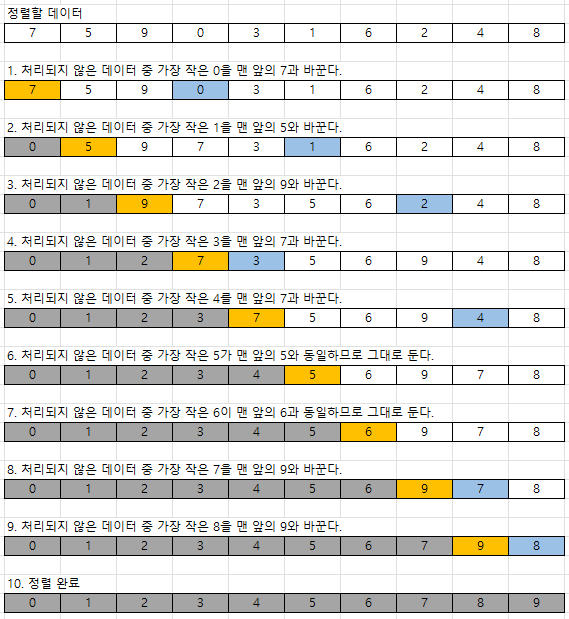
파이썬으로 구현하기
array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]
for i in range(len(array)):
min_index = i # 가장 작은 원소의 인덱스
for j in range(i + 1, len(array)):
if array[min_index] > array[j]:
min_index = j
array[i], array[min_index] = array[min_index], array[i] # 스와프
print(array)[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]효율성
N개의 데이터를 선택정렬한다고 하면, 연산 횟수는 아래와 같다.
N + (N-1) + (N-2) + ... + 2 = N * (N+1) / 2따라서 시간복잡도는 O(N^2)으로 나타낼 수 있다.
데이터의 개수가 많아지면 속도가 급격히 느려지며, 다른 정렬 알고리즘에 비해 비효율적인 편이다.
대신 특정 리스트에서 가장 작은 값을 찾을때 자주 쓰인다.
2. 삽입정렬 (Insertion Sort)
처리되지 않은 데이터를 하나씩 골라 적절한 위치에 삽입하는 방법
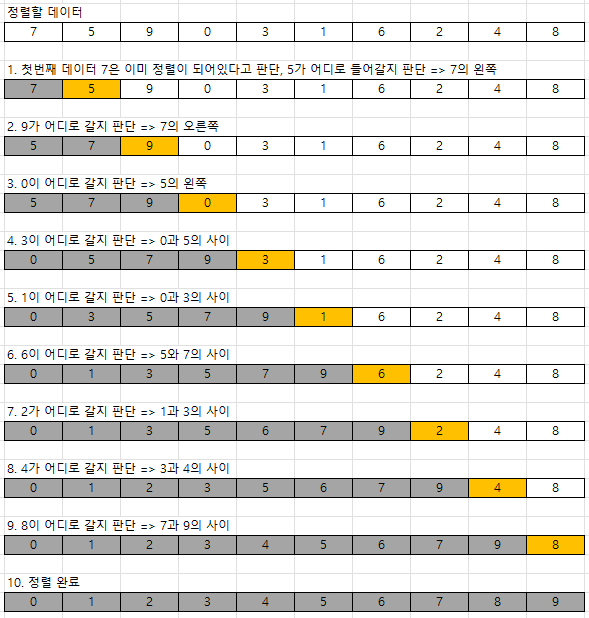
파이썬으로 구현하기
array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]
for i in range(1, len(array)):
for j in range(i, 0, -1): # 인덱스 i부터 1까지 1씩 감소하며 반복하는 문법
if array[j] < array[j - 1]: # 한 칸씩 왼쪽으로 이동
array[j], array[j - 1] = array[j - 1], array[j]
else: # 자기보다 작은 데이터를 만나면 그 위치에서 멈춤
break
print(array)[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]적절한 위치를 찾기 위해 자기보다 더 작은게 나올때까지 계속 swap해가며 거꾸로 내려간다.
효율성
시간복잡도는 선택정렬과 마찬가지로 O(N^2)이지만, 현재 리스트가 거의 정렬되어있는 상태라면 매우 빠르게 동작한다. (최선의 경우 O(N))
3. 퀵정렬 (Quick Sort)
기준 데이터를 설정하고, 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾸는 방법
일반적인 상황에서 가장 많이 사용되며, 기본적인 퀵정렬은 첫번째 데이터를 기준데이터(pivot)로 설정한다.
기준값으로부터 큰수들은 오른쪽으로, 작은수들은 왼쪽으로 정렬하며 동작한다.

파이썬으로 구현하기
array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]
def quick_sort(array):
# 리스트가 하나 이하의 원소만을 담고 있다면 종료
if len(array) <= 1:
return array
pivot = array[0] # 피벗은 첫 번째 원소
tail = array[1:] # 피벗을 제외한 리스트
left_side = [x for x in tail if x <= pivot] # 분할된 왼쪽 부분
right_side = [x for x in tail if x > pivot] # 분할된 오른쪽 부분
# 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬을 수행하고, 전체 리스트를 반환
return quick_sort(left_side) + [pivot] + quick_sort(right_side)
print(quick_sort(array))[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]효율성
퀵정렬의 평균 시간복잡도는 O(NlogN)이지만, 최악의 경우에는 선택정렬과 삽입정렬과 마찬가지로 O(N^2)이다.
무작위로 입력된 데이터의 경우에는 효율적이지만, 이미 데이터가 정렬되어있는 경우에는 매우 느리고, 이럴때는 삽입정렬을 쓰는게 더 효율적이다.
4. 계수정렬 (Count Sort)
특정한 조건이 부합할때만 사용할 수 있지만 매우 빠르게 동작한다.
데이터의 크기 범위가 제한되기 때문에 정수 형태로 표현할 수 있을때만 사용 가능하다.
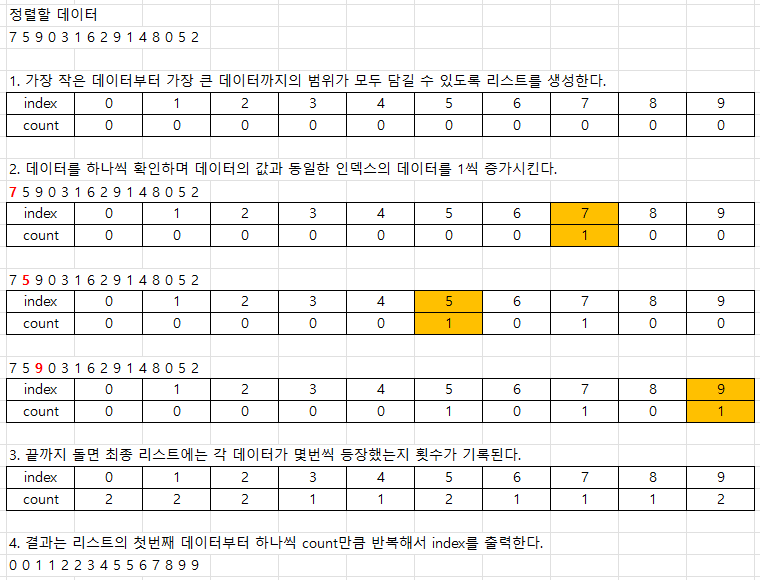
파이썬으로 구현하기
# 모든 원소의 값이 0보다 크거나 같다고 가정
array = [7, 5, 9, 0, 3, 1, 6, 2, 9, 1, 4, 8, 0, 5, 2]
# 모든 범위를 포함하는 리스트 선언 (모든 값은 0으로 초기화)
count = [0] * (max(array) + 1)
for i in range(len(array)):
count[array[i]] += 1 # 각 데이터에 해당하는 인덱스의 값 증가
for i in range(len(count)): # 리스트에 기록된 정렬 정보 확인
for j in range(count[i]):
print(i, end=' ') # 띄어쓰기를 구분으로 등장한 횟수만큼 인덱스 출력0 0 1 1 2 2 3 4 5 5 6 7 8 9 9효율성
데이터의 개수가 N개, 데이터(양수) 중 최대값이 K일때 최악의 경우에도 시간복잡도 O(N+K)를 보장한다.
하지만 경우에 따라 심각하게 비효율적일 수 있다. (ex. 데이터가 0과 999,999로 2개만 존재하는 경우)
동일한 데이터가 여러번 반복되어 나타날때 효과적으로 사용할 수 있다.
5. 버블정렬 (Bubble Sort)
서로 인접한 2개의 데이터를 비교해서 크기가 순서대로 되어있지 않으면 서로 교환하는 방법
1회전을 수행하고 나면 맨 뒤에는 가장 큰 데이터가 있게 되고, 이는 다음 정렬에서 제외된다.
2회전을 수행하고 나면 맨 뒤에서 2번째에 2번째로 큰 데이터가 있게 되고, 이는 다음 정렬에서 제외된다.
이렇게 모두 정렬될때까지 반복한다.

효율성
구현이 간단하고 시간복잡도는 O(N^2)이다.
6. 합병정렬 (Merge Sort)
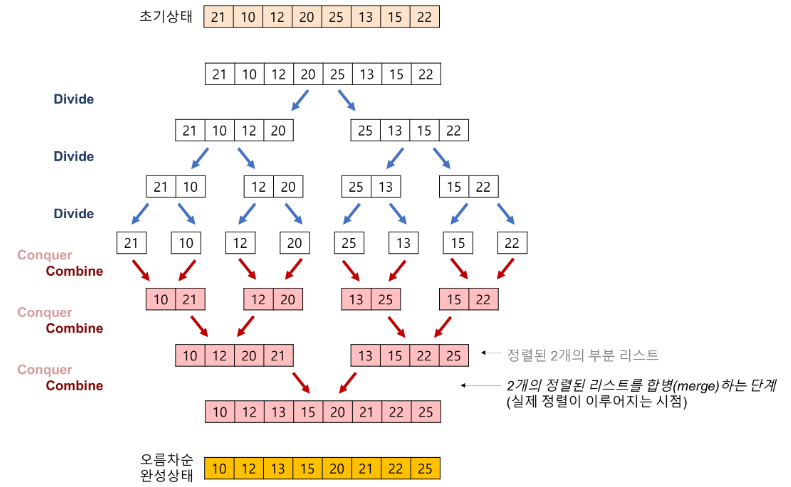
분할정복(Divide and Conquer : 큰 문제를 반으로 쪼개 문제를 해결해나가는 방식) 방식으로 설계된 알고리즘
-
분할과정
(1) 현재 배열을 반으로 쪼갠다. (기준 = (시작위치 + 종료위치) / 2)
(2) 쪼갠 배열의 크기가 0이나 1일때까지 반복한다. -
합병과정
(1) 두 배열 A, B의 크기를 비교한다.
(2) i = A배열의 시작인덱스, j = B배열의 시작인덱스
(3) A[i]와 B[j]를 비교하여 둘 중 작은 값을 새배열 C에 저장한다. (오름차순)
(4) i나 j중 하나가 각자 배열의 끝에 도달할때까지 반복한다.
(5) 배열의 끝에 도달하지 못했다면 그대로 C에 붙인다.
(6) C배열을 원래 배열에 저장한다.
효율성
전체 배열의 길이가 N일때, 분할과정에서는 단순 쪼개기이므로 따로 시간복잡도가 발생하지 않지만 합병과정에서는 시간복잡도가 O(N)이다. 그러나 분할과정만큼 합병과정도 똑같이 일어나는데, 분할과정이 logN번 일어나므로 합병정렬의 전체 시간복잡도는 O(NlogN)이다.
파이썬 기본 정렬 라이브러리 sorted()
파이썬의 기본 정렬 라이브러리인 sorted()는 퀵정렬과 비슷한 병합정렬을 기반으로 만들어졌으며, 최악의 경우에도 시간복잡도 O(NlogN)를 보장한다.
코드
1. 가장 큰수 (Lv. 2)
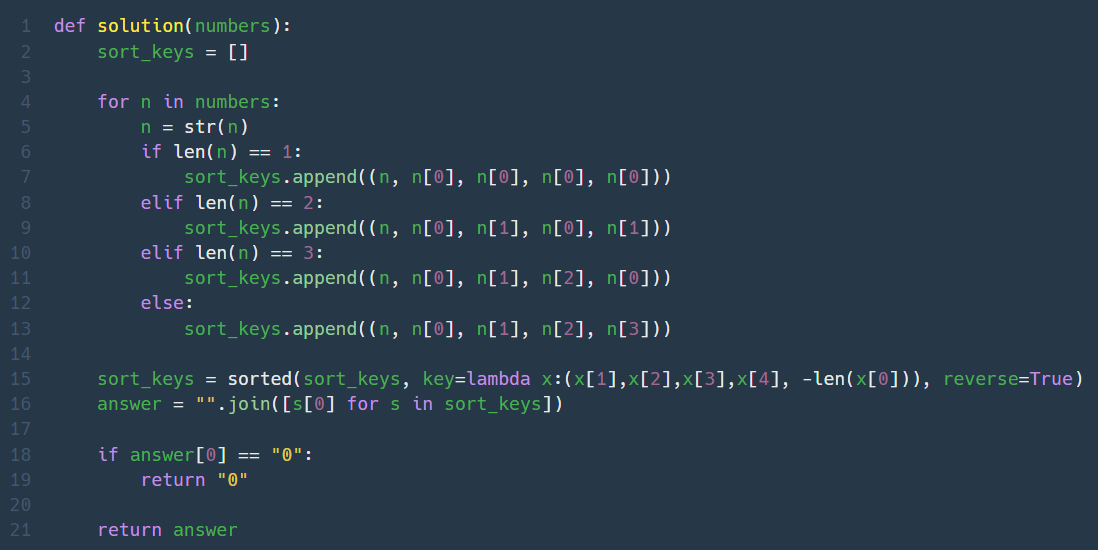
숫자를 문자열로 바꿔서 3번 반복하고 사전순으로 나열하면 숫자의 3자릿수까지 사전순으로 비교가 가능하다는 것이 핵심 원리였는데...... 로직은 똑같았는데 비교 기준을 잘못찾아서 헤맸다.
맨 앞의 자릿수가 큰것부터 정렬하는데, 맨 앞자릿수가 똑같다면 그 다음에는 두번째 자릿수끼리 비교해서 큰 것, 그 다음에는 세번째 자릿수끼리 비교해서 큰 것을 우선으로 한다. 이때 숫자마다 길이가 다르므로, 적절한 비교를 위해서 숫자를 3번 반복한다. (ex. 3=>333, 31=>313131)
다른사람들 코드⬇️
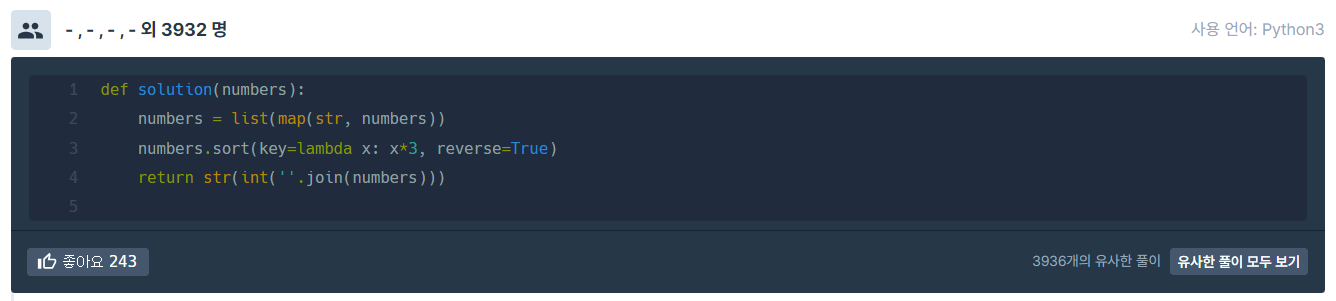
2. H-Index (Lv. 2)
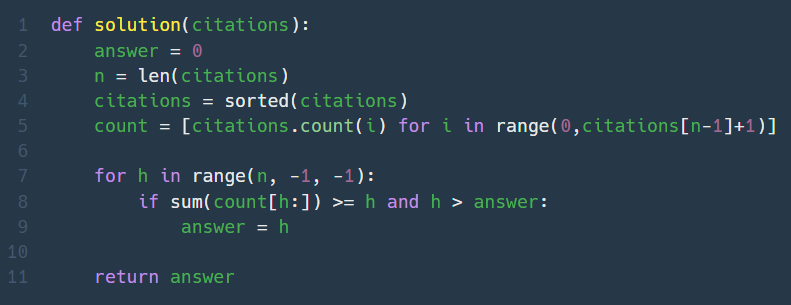
얘도 문제가 애매하게 가독성이 똥망 ㅡ.ㅡ
n부터 거꾸로 0까지 가면서 문제의 조건에 맞는 h를 찾는다. 이때 h는 citations에도, n에도 존재하지 않는 숫자일수 있다.
count()는 존재하지 않는 원소의 개수를 찾을때도 에러가 안나고 0이 반환된다.
느낀점
- 위에서 열심히 찾아서 정리한 정렬 알고리즘이랑 코테 정렬문제랑은 결이 전혀...... 다르다. 정렬 자체는 그냥 기본 라이브러리인
sorted()를 쓰면 되고 정렬을 어떤 방식으로 하면 문제가 풀릴것인지를 고민해야하더라.
