
📌 "이분탐색 기법을 이용해 효율적으로 값을 찾아보세요"
출제빈도 : 낮음
평균점수 : 낮음
이분탐색(Binary Search, 이진탐색)이란?
정렬된 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법
❗데이터가 모두 정렬되어 있어야만 사용할 수 있다.
찾으려는 데이터(target)와 탐색범위([start, end])의 중간에 위치한 데이터(mid)를 반복적으로 비교해서 원하는 데이터를 찾는다.
시간복잡도 : O(logN)
이분탐색 진행과정
- 탐색범위(
[start, end])의 중간값(mid)을 선택해서 찾고자 하는 값(target)과 일치하는지 확인한다. if mid == target: 해당값을 반환한다.if mid < target: 탐색범위를 큰 쪽으로 잡는다. (start = mid + 1)if mid > target: 탐색범위를 작은 쪽으로 잡는다. (end = mid - 1)- 원하는 값이 나올때까지 1~4번을 반복한다.
- 더 이상 검사할 곳이 없으면(
if start > end) 종료한다.

이분탐색 구현하기 (1) - 반복문
target = 25
search_list = [30, 94, 27, 92, 21, 37, 25, 47, 25, 53, 98, 19, 32, 32, 7]
search_list.sort()
start = 0
end = len(search_list)-1
while start <= end:
mid = (start + end) // 2
if search_list[mid] == target:
print(mid)
break
elif search_list[mid] > target:
end = mid - 1
else:
start = mid + 13 # [7, 19, 21, "25", 25, 27, 30, 32, ... ]이분탐색 구현하기 (2) - 재귀
def binary_search(array, target, start, end):
mid = (start + end) // 2
if target == array[mid]:
print(mid)
elif array[mid] > target:
binary_search(array, target, start, mid - 1)
elif array[mid] < target:
binary_search(array, target, mid + 1, end)
else:
return False
target = 25
search_list = [30, 94, 27, 92, 21, 37, 25, 47, 25, 53, 98, 19, 32, 32, 7]
search_list.sort()
start = 0
end = len(search_list)-1
binary_search(search_list, target, start, end)3 # [7, 19, 21, "25", 25, 27, 30, 32, ... ]이분탐색 구현하기 (3) - bisect 라이브러리
import bisect
bisect_left(정렬된 리스트, 타겟): 정렬된 리스트에서 타겟을 삽입할때 들어갈 수 있는 가장 왼쪽 인덱스bisect_right(정렬된 리스트, 타겟): 정렬된 리스트에서 타겟을 삽입할때 들어갈 수 있는 가장 오른쪽 인덱스
import bisect
target = 25
search_list = [30, 94, 27, 92, 21, 37, 25, 47, 25, 53, 98, 19, 32, 32, 7]
search_list.sort()
print(bisect.bisect_left(search_list, target))
print(bisect.bisect_right(search_list, target))3 # [7, 19, 21, (여기), 25, 25, 27, 30, 32, ... ]
5 # [7, 19, 21, 25, 25, (여기), 27, 30, 32, ... ]💡
search_list에target이 몇개 있는지 알고 싶다면?
bisect_right(search_list, target) - bisect_left(search_list, target)
코드
1. 입국심사 (Lv. 3)
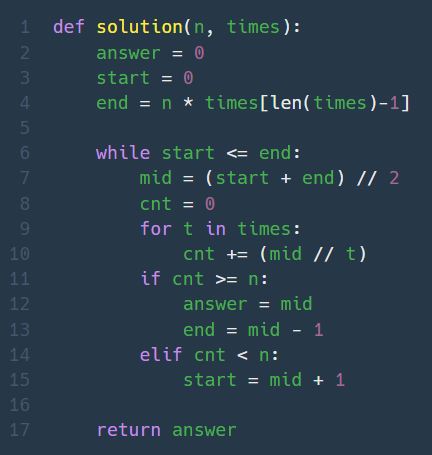
문제 자체가 어려운건 아닌거 같은데 딱봐도 내맘대로 풀면 시간초과일거라고 협박하는 듯한 제한사항의 1,000,000,000명이라는 숫자와.. 아무리 생각해도 이분탐색 알고리즘과 문제가 매치가 안돼서 도대체 어떻게 이게 이분탐색 문제인거지?? 하면서 풀이를 찾아봤다. 한가지 위안인 점 : 구글링할때 이 문제 이분탐색 풀이 감을 못잡았다는 글이 많았다 나만 그런게 아녔어
정말 상상도 못한 아이디어.. ㄴㅇㄱ
구해야하는 것 = 모든 사람이 심사를 받는데 걸리는 "최소" 시간
모든 사람이 심사를 받는데 "시간이 가장 적게" 걸리려면, 같은 시간내에 "최대한 많은 사람"을 심사해야한다.
다시말해, 일정 시간동안 최대한 많은 사람을 심사하려면 모든 심사대에서 쉬지않고 계속 심사를 해야한다. 예를들어 심사대가 3개가 있는데 각각 심사시간이 2분, 3분, 4분(times = [2,3,4])이라면, 10분동안 최대한 많이 심사할 수 있는 사람의 수는 2분짜리 심사대에서 5명(10 // 2 = 5), 3분짜리 심사대에서 3명(10 // 3 = 3), 4분짜리 심사대에서 2명(10 // 4 = 2), 해서 총 10명이다.
가능한 모든 시간에 대해서 위 계산을 진행하려면 그 범위는 다음과 같다.
start= 0end= 심사시간이 가장 긴 심사대 1개에서 n명을 모두 심사하는 시간 =times[len(times) - 1] * n
그리고 [start, end]의 범위에 해당하는 시간동안, 이분탐색을 사용해 n명을 모두 심사할 수 있는 최소시간을 찾으면 답이다.
mid 시간동안 최대로 심사할 수 있는 사람의 수(cnt)를 구하고,
cnt<n이라면,mid시간동안n명을 모두 처리할 수 없다는 뜻이므로 탐색범위를 큰쪽(오른쪽)으로 옮긴다. =>start = mid + 1cnt>=n이라면,mid시간동안n명보다 많은 사람을 처리할 수 있다는 뜻이므로, 탐색범위를 작은쪽(왼쪽)으로 옮긴다. =>end = mid - 1- 💡 여기서 주의깊게 볼 부분은
cnt > n이 아니라cnt >= n이라는 점이다. 원래대로라면cnt == n일 때를 따로 빼서 정답을 반환하겠지만, 문제 특성상 이 값이 정확히 맞아떨어지지 않을 수 있고, 여분의 시간을 남긴채로 종료하는게 최선의 선택일 수 있다. 그렇기 때문에 범위를 좁힘과 동시에 혹시 모르니 정답을 옮겨두고 (=>answer = mid) 끝까지 탐색하는 것이다.
- 💡 여기서 주의깊게 볼 부분은
풀이 떠올리기가 쉽지 않은데, 정작 구현은 되게 깔끔한 문제였다.
2. 징검다리 (Lv. 4)
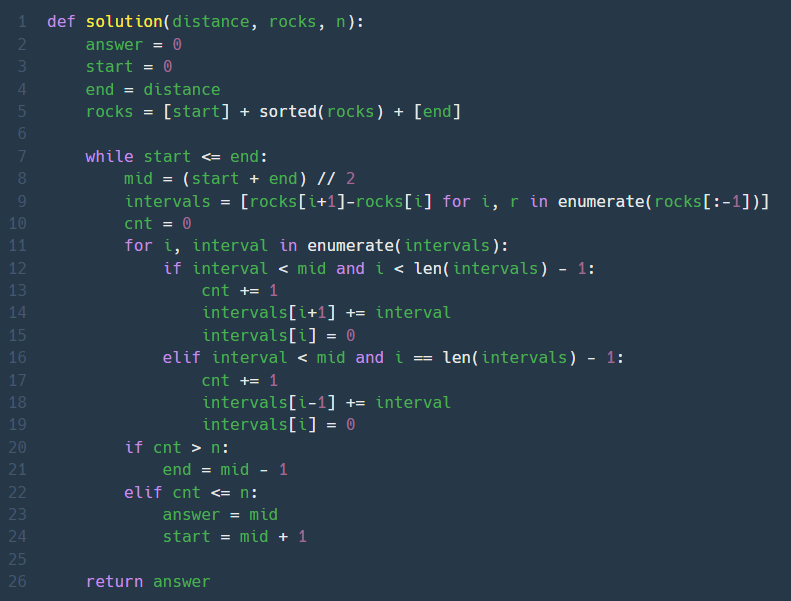
얼마만에 스스로 수월하게 푼 문제인지 엉엉엉엉
입국심사 문제 풀면서 생긴 감으로 이 문제도 처음부터 이분탐색에 맞춰서 생각했다.
-
구해야하는것 = "바위 사이 간격의 최소값" 중 최대값
-> 탐색범위 = "바위 사이 간격의 최소값"이 될 수 있는 수들 = 바위를 1개, 2개, ... 모두 제거했을때 나올 수 있는 바위 사이 간격의 최소값들 (cf. 바위를 적게 제거할수록 간격이 작고, 많이 제거할수록 간격이 넓어진다.) -
주어진 것 = 바위의 위치, 제거해야하는 바위의 수
-> 탐색타겟 = 제거해야하는 바위의 수
그렇다면 탐색범위인 "바위 사이 간격의 최소값"으로부터 "제거해야하는 바위의 수"를 구해야 탐색타겟과 비교를 할 수가 있겠지?
"바위 사이 간격의 최소값"이 N이어야 할때, 제거해야하는 바위의 수를 구하는 방법
: 앞에서부터 바로 뒤에 있는 바위와의 간격을 보고, 이 간격이 N보다 작으면 뒤에 있는 바위를 제거하고 제거한 바위와 그 뒤에 있는 바위 사이의 간격에 현재간격을 포함시키도록 값을 업데이트한다. 이 과정을 몇번 반복하는지가 제거해야하는 바위의 수이다.
좀 복잡한데 그림으로 나타내면 다음과 같다.
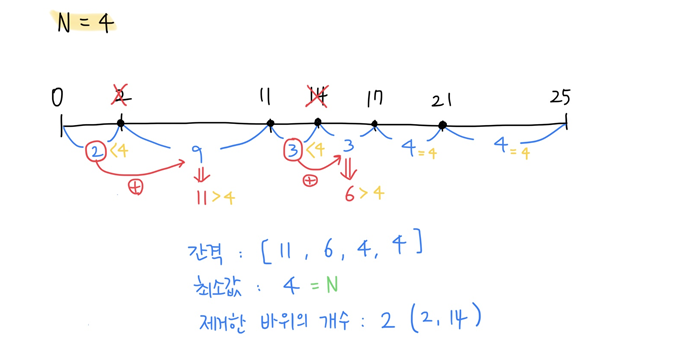
바위 간격의 최소값이 4여야하기 때문에, 간격이 4보다 작은 경우에는 바위를 제거해서 간격이 4보다 커지도록 늘려야한다.
0 ~ 2: 간격=2가 4보다 작으므로, 2번 바위 제거 후 다음에 살펴볼2 ~ 11간격에0 ~ 2간격을 더한다.2 ~ 11: 간격=9이지만 1번과정에서 2번 바위가 제거되어0 ~ 2까지 포함해 사실상0 ~ 11이다. 따라서 간격=11, 이는 4보다 크므로 패스한다.11 ~ 14: 간격=3이 4보다 작으므로, 14번 바위 제거 후 다음에 살펴볼14 ~ 17간격에11 ~ 14간격을 더한다.14 ~ 17: 간격=3으로 4보다 작지만 3번과정에서 14번 바위가 제거되어11 ~ 14까지 포함해 사실상11 ~ 17이다. 따라서 간격=6, 이는 4보다 크므로 패스한다.17 ~ 21: 간격=4는 4와 동일하므로 패스한다.21 ~ 25: 간격=4는 4와 동일하므로 패스한다.
그럼 2개의 바위를 제거한 후 남은 바위끼리의 간격은 [11, 6, 4, 4]가 되고, 최소값은 4로, N=4를 만족한다.
이제 다시 이분탐색으로 돌아와서,
- 탐색범위
[0, distance]에서mid를 골라, 바위 사이의 간격의 최소값이mid가 되기위해 제거해야하는 바위의 수(cnt)를 계산한다. cnt > n이라면, 문제에서 주어진 제거해야할 바위의 수보다 많이 제거해야 최소간격이mid가 된다는 뜻이므로, 탐색범위를 제거할 바위가 적은 쪽(왼쪽)으로 좁힌다. =>end = mid - 1cnt <= n이라면, 문제에서 주어진 제거해야할 바위의 수보다 적게 제거해서 최소간격이mid가 됐다는 뜻이므로, 탐색범위를 제거할 바위가 많은 쪽(오른쪽)으로 좁힌다. =>start = mid + 1
💡 그리고 이번에도cnt와n이 딱 맞아떨어지지 않을 수 있기 때문에, (바위를 최소cnt개만 제거해도 최소간격이mid가 되는데, 문제에서n개를 제거해야한다고 나와있다면, 그냥 아무 바위나 마저 더 제거하면 된다.)answer를 이때 저장해두고 다음탐색을 진행했다.
하면 끝!
느낀점
- 구현 자체는 이분탐색의 고정틀에서 벗어나지 않는다. 대신 완전 아이디어 떠올리기 싸움인 것 같다. 이분탐색에 맞춘 풀이 아이디어 떠올리기가 쉽지 않음...
- 구해야하는 것으로부터 탐색범위를, 주어진 것으로부터 탐색타겟을 연상하도록 한다. 그리고 탐색범위 안에 있는 데이터로부터 탐색타겟을 어떻게 도출해낼 건지도 잘 생각해야한다.
- 현재값이 타겟값인지 확인하기 위해 반복문 등을 통해 계산하는 과정은 필요하다. 대신 이 과정을 실행하는 횟수를 이분탐색을 통해 확! 줄여버리는게 중요한 포인트다.
- 문제에 ~한 것중에 최대값, ~한 것중에 최소값을 구하라는 형식이 많아서 정렬, min, max로 생각이 빠지기 쉬운데..... 제한사항에 터무니없이 큰 숫자가 있다면.. 이분탐색 의심해보기
- 이분탐색으로 최소/최대값을 구하라는건, 모든 경우에 가능한 모든 수들을 나열해놓고, 이 중에서 문제조건을 만족하는 최소/최대값을 찾으라는거다. 문제조건에 만족하는 수들을 늘어놓고 최소/최대값을 찾으라는게 아니다!!
- 조금 꼬아서 비유하면
[2,4,10]이 있을때, 이중 최대값은10이지만, 이러저러한 문제조건을 만족하는 최대값은4이므로 답은4인 것
- 조금 꼬아서 비유하면
