
📌 "힙은 특정한 규칙을 가지는 트리로, 힙을 이용해서 우선순위 큐를 구현할 수 있습니다."
출제빈도 : 보통
평균점수 : 높음
많은 언어에서 이미 구현된 우선순위 큐 라이브러리를 제공합니다. 이를 활용하면 효율적으로 문제를 풀 수 있습니다. 우선순위 큐를 이용해서 해결하기에 적합한 문제들을 만나보세요.
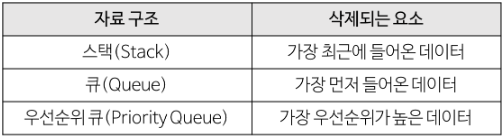
우선순위 큐(Priority Queue)란?
- 먼저 들어오는 데이터가 먼저 나가는 일반 큐와 달리, 우선순위가 높은 데이터가 먼저 나가는 자료구조
- 일반적으로 힙을 이용하여 구현한다.
힙(Heap)이란?
- 우선순위 큐를 위해 만들어진 자료구조
- 완전 이진 트리의 일종
- 여러 값들 중에서 최대값/최소값을 빠르게 찾을 수 있다.
cf) 완전 이진 트리 : 높이가 h일때, 레벨 h-1까지는 빈곳없이 꽉 차 있고, 레벨 h에서는 왼쪽부터 노드가 순서대로 채워진 이진트리

최대힙 (Max Heap)
: 부모노드의 키값이 자식노드보다 크거나 같은 완전이진트리

최소힙 (Min Heap)
: 부모노드의 키값이 자식노드보다 작거나 같은 완전이진트리
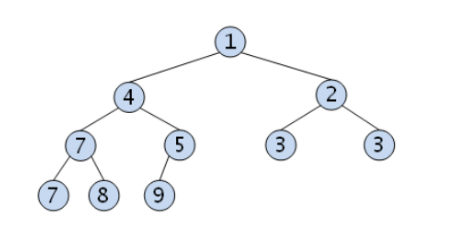
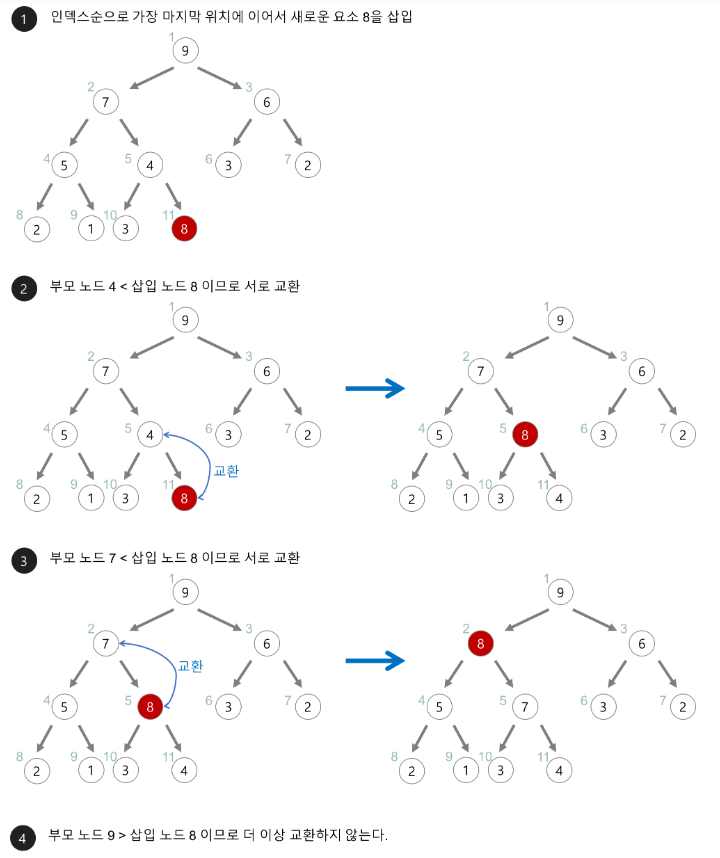
힙의 삽입
- 힙의 새로운 요소는 일단 마지막 노드에 이어서 삽입한다.
- 새로운 노드를 부모 노드들과 비교하고 교환해서 힙의 성질을 만족시키도록 재구성한다.
힙의 삭제
최대힙에서는 최대값을, 최소힙에서는 최소값만을 삭제할 수 있다.
- 루트 노드를 삭제한다.
- 삭제된 루트 노드에 힙의 마지막 노드를 가져온다.
- 힙의 성질을 만족시키도록 자식과 교환하며 재구성한다.

파이썬에서 힙 구현하기
최소힙 구현하기
- 파이썬에서는
heapq모듈을 통해 최소힙(min heap)을 사용한다. - 인덱스 0에서 시작해
k번째 원소가 항상 자식 원소들(2k+1,2k+2)보다 작거나 같은 최소힙의 형태로 정렬된다.
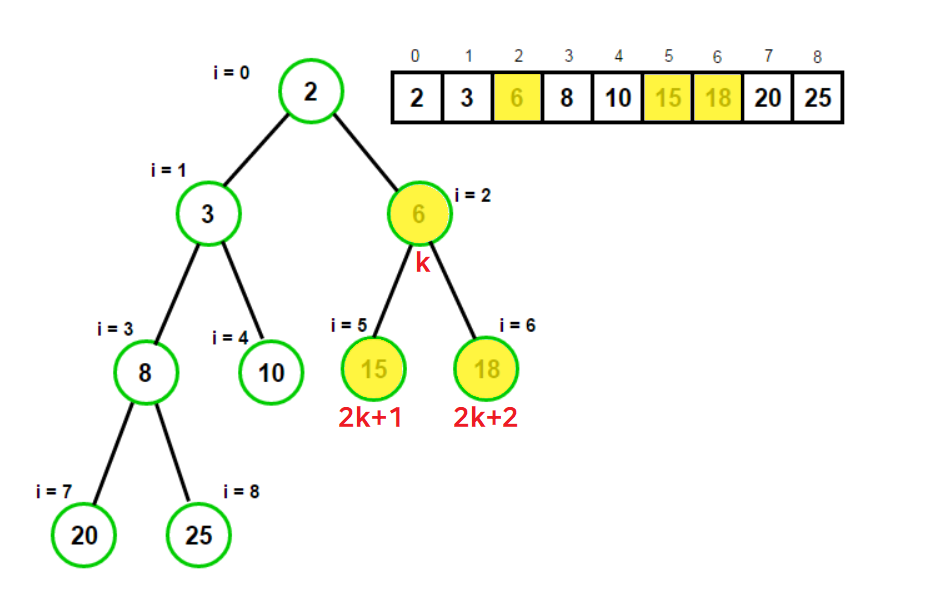
heapq모듈은 리스트를 최소힙처럼 다룰 수 있게 해준다.
import heapq
heap = [] # 빈 heap 선언
heapq.heappush(heap, item) # heap에 item을 추가한다.
heapq.heappop(heap) # heap에서 가장 작은 원소를 삭제 & 리턴한다. (비어있는 경우 IndexError 발생)
heapq.heapify(x) # 리스트 x를 바로 heap으로 변환한다. (O(N))
heap[0] # heap에서 원소를 삭제하지 않고 가져온다.최대힙 구현하기
- 파이썬에서 최대힙을 사용하려면 최소힙에 변형을 줘야 한다.
- 힙에 원소를 추가할때
(-item, item)과 같이 튜플로 넣으면 튜플의 첫번째 원소를 우선순위로 힙을 구성한다. 두번째 원소는 원본값 보존을 위해 가지고 간다. 이후 값에 접근할때 [1] 인덱싱을 통해 접근한다.
import heapq
max_heap = []
for item in [1,3,5,7,9]:
heapq.heappush(max_heap, (-item, item)) # 최대힙 구성
# [(-9, 9), (-7, 7), (-3, 3), (-1, 1), (-5, 5)]
heapq.heappop(max_heap)[1] # 최대힙에서 가장 큰 원소
# 9코드
1. 더 맵게 (Lv. 2)
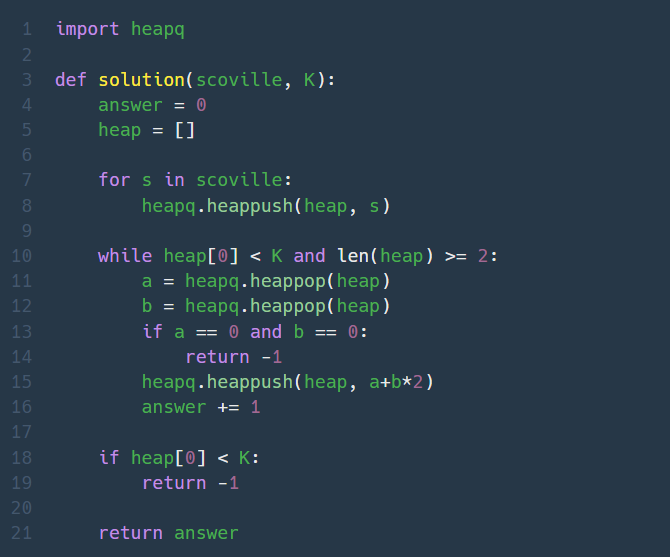
스코빌 지수를 최소힙으로 만든다. 그리고 가장 작은 수 2개, 즉 루트노드를 2번 pop시킨 다음, 주어진 식에 맞춰 변형한 다음 힙에 추가하는 과정을 반복한다.
2. 디스크 컨트롤러 (Lv. 3)
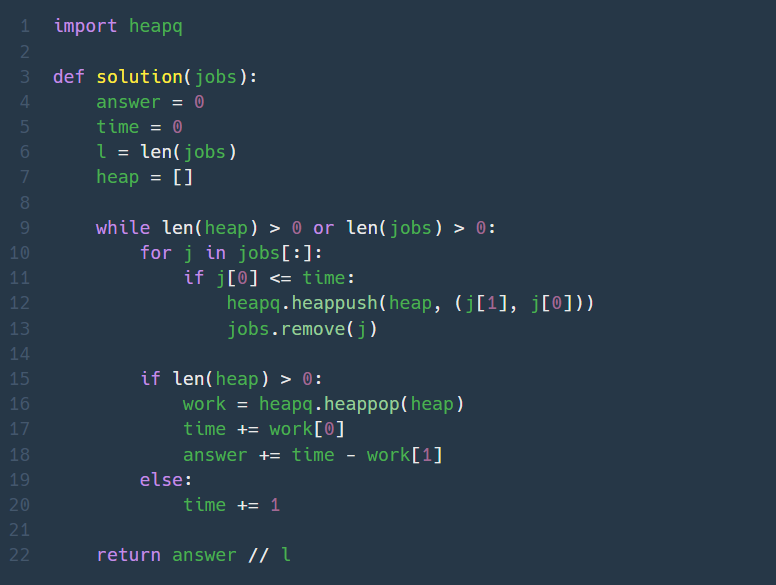
jobs에는 요청 전의 작업이, heap에는 요청되고 대기 중인 작업이 들어간다.
현재 시간을 기준으로 요청 시간이 지난 상태라면 작업 시간을 기준으로 최소힙인 heap에 추가하고(작업시간이 가장 짧은 작업이 루트노드가 된다), jobs에서는 제거한다.
heap에 대기중인 작업이 있다면 pop시켜서 해당 작업이 끝났을때의 시간으로 워프한다. 그리고 현재시간(=작업이 끝난 시간)에서 해당 작업의 요청시간을 빼서 요청부터 종료까지 얼만큼 걸렸는지 계산한다. 대기중인 작업이 없었다면 시간은 원래대로 1만큼씩만 흐른다.
3. 이중우선순위큐 (Lv. 3)

min_heap과 max_heap을 각각 만들어서 최소값/최대값을 찾으려고 했는데, 두 힙을 동기화시키는 방법이 생각이 안나서 위와 같이 힙과 리스트를 짬뽕시켜서 풀었다.
삽입과 최소값 삭제는 heappush와 heappop을 이용해 간단하게 구현했고, 최대값 삭제는 배열에서 최대값을 찾아 remove로 제거한 후에 힙의 성질을 유지시키기 위해 heapify를 한번 더 해주었다.
다른 사람들의 풀이를 봐도 max_heap과 min_heap을 깔끔하게 동시 사용하는 코드는 없는 듯하다.
느낀점
[0]이 무조건 최소값/최대값이라는게 아주 편한듯하다.- 파이썬에서는 리스트를 힙으로 사용하는거라 힙으로 풀거긴 하지만 리스트로서의 성질도 사용할 수 있다.
