백준 11505번 골드1
해당 문제를 선형탐색으로 풀고 쉽네 ㅎㅎ 라고 했다가
시간 초과가 걸렸다..
이 문제는 세그먼트 트리로 풀어야 하는 유형이다.
먼저 세그먼트 트리의 개념에 대해서 알아가보자!
🔢 세그먼트 트리
연속된 구간의 데이터의 합을 가장 빠르고 간단하게 구할 수 있는 트리
내가 했던 것처럼 선형 탐색을 통해 해당 문제를 푼다면, 시간복잡도 O(n)으로 속도가 느리다는 단점이 있다. 즉 10만개의 데이터에서 1만개의 구간 합을 구하려면 10억번의 연산을 해야한다는 의미이다.
세그먼트 트리로 합을 구하면 시간 복잡도가 O(logN)이 된다!
🔢 구간 합 트리 생성
기존의 배열 [1 2 3 4 5]을 트리구조를 이용하여 구간 합 트리를 생성해본다.
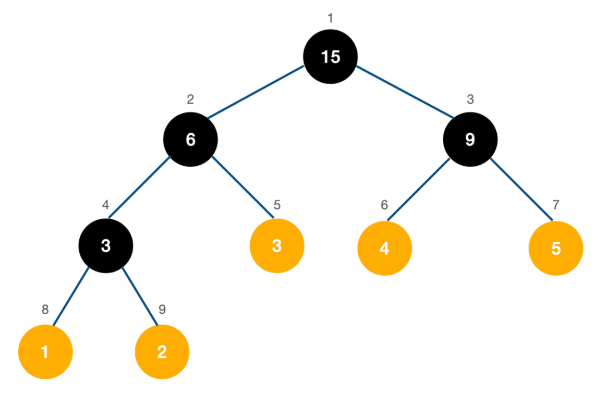
재귀적으로 탐색하여 stack 방식을 이용해보자.
🧠 콜 스택(Call Stack)이란?
함수가 호출될 때 마다, 그 함수의 정보가 스택에 저장됨
함수가 끝나면, 스택에서 pop 되어 빠져나감
재귀는 이 스택을 통해 깊이 우선 탐색(DFS) 방식으로 처리됨
static long pSum(int start, int end, int node, int l, int r) {
if(r < start || l> end ) return 0;
if(l <= start && end <= r )return tree[node];
int mid = (start+end)/2;
return pSum(start, mid, node*2, l, r) + pSum(mid+1, end, node*2+1, l, r);
}- 트리 노드가 담당하는 구간이 l~r과 겹치지 않으면, 합에 영향이 없으니 0 반환
- 해당 구간이 l~r에 완전히 포함되면, 해당 구간의 합이 이미 tree[node]에 저장되어 있으므로 그냥 반환
- 일부분만 겹칠 경우!
- 현재 구간을 왼쪽, 오른쪽으로 나눠서 각각 재귀 호출
- 합을 더해서 반환 (왼쪽 구간 + 오른쪽 구간)
- 완전 이진 트리 구조의 특징: 왼쪽 자식
node*2, 오른쪽 자식node*2+1
🔢 배열 크기의 최댓값
이쯤되면, 구간 합 트리는 이진 트리임을 알 수 있다. 이진 트리 중 모든 노드가 꽉 차있는 완전 이진트리일 경우 가장 많은 데이터를 가진다. 그래서 배열의 크기 N이 주어졌을 때, 완전 이진 트리의 크기를 구하면 된다.
완전 이진트리 특성 상
h>=1, 2^(h-1)< N <= 2^h가 성립하므로 각 항에 log2를 넣어주면 높이 h-1 < log2(N) <= h임을 알 수 있다.
여기서 높이를 구하는 이유는?
노드 수가 N개일 때, 트리를 표현하려면 배열의 크기를 미리 정해야 한다.
그러려면! 이진 트리의 높이가 필요하다.
// log2(N)
int h = (int) Math.ceil(Math.log(N) / Math.log(2));위 코드는 N개의 데이터를 담기 위한 세그먼트 트리의 최소 높이이다.
🔢 이진 트리의 전체 노드 수
이진트리의 높이가 h일 때, 전체 노드 수는 2^(h+1) - 1이다.
여기서 h+1이 되는 이유는 h는 트리의 "깊이"인데, 루트부터 시작해서 0 ~ h까지 총 h+1층이 있기 때문이다.
위 공식을 코드에 반영해본다면
int treeSize = (int) Math.pow(2, h + 1) - 1;하지만 세그먼트 트리를 사용할 때에는 루트노드 index를 1로 저장해줄 것이기 때문에 +1을 사용하여 배열 크기를 생성해주면 된다.
// 루트 노드 index 1로 시작 할 경우 size+1
int treeSize = (int)Math.pow(2, h + 1);현재까지 언급한 공식을 정리하면 아래와 같다
- 리프 노드 수: N (입력 데이터 수)
- 트리 높이: h = ceil(log₂(N))
- 트리 전체 노드 수: 2^(h+1) - 1
🔢 구간 합 update
배열에 있는 특정 원소의 값을 수정할 때에는 해당 원소를 포함하고 있는 모든 구간의 합 노드들을 갱신해야 한다.
예를 들어 [ 1 2 3 4 5 ]을 [ 1 2 6 4 5 ]로 바꾸면 구간 합 트리는 다음과 같이 update되어야 한다.
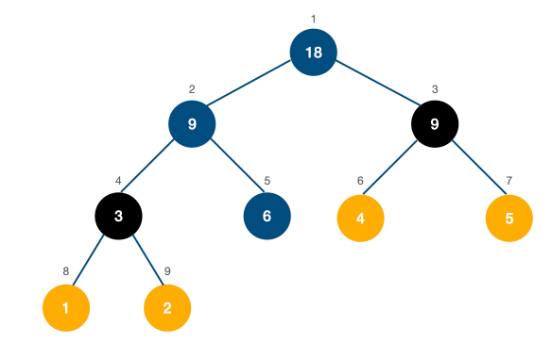
해당 함수도 재귀적 탐색을 통해 변경하면 된다. 트리를 탐색하면서 idx(변경이 일어난 인덱스)를 포함하고 있는 곳들을 찾아 갱신해주면 된다. if (start <= idx && idx <= end)
💡 예시 상황
배열 arr[2] = 3 이었는데, 6으로 바꿨다면?
그럼 dif = 6 - 3 = 3
트리에 저장된 구간 합도 +3씩 갱신해야한다. 이걸 재귀적으로 쭉 내려가면서 트리 값들을 수정해주는 함수를 만들면 된다.
// 배열 idx =2
// 변경값 dif = (새로운 값 - 원래 값) = 6 - 3 = 3
// node = 현재 트리 노드 번호 (tree 배열의 인덱스)
static void update(int start, int end, int node, int idx, long dif) {
if (start <= idx && idx <= end) // 포함되면 dif만 더하기
tree[node] += dif;
else // 해당 구간에 포함이 안 된다면
return;
// 길이가 1짜리인 노드 즉, 리프 노드까지 내려온 경우
// 더 이상 탐색할 필요 없으니 return
if (start == end) return;
// 현재 구간을 반으로 나눠서 왼쪽 자식 / 오른쪽 자식
// 각각 재귀적으로 호출해서 idx가 포함된 쪽만 업데이트
int mid = (start+end)/2;
update(start, mid, node*2, idx, dif);
update(mid+1, end, node*2+1, idx, dif);
}전체 코드
import java.io.*;
import java.util.*;
public class BOJ_11505 {
static int N, M, K;
static long[] arr, tree;
static final long MOD = 1_000_000_007;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
arr = new long[N];
for (int i = 0; i < N; i++) {
arr[i] = Long.parseLong(br.readLine());
}
int h = (int) Math.ceil(Math.log(N) / Math.log(2));
int treeSize = 1 << (h + 1);
tree = new long[treeSize];
init(1, 0, N - 1);
StringBuilder sb = new StringBuilder();
for (int i = 0; i < M + K; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
if (a == 1) {
update(1, 0, N - 1, b - 1, c);
} else {
sb.append(query(1, 0, N - 1, b - 1, c - 1)).append("\n");
}
}
System.out.print(sb);
}
static long init(int node, int start, int end) {
if (start == end) return tree[node] = arr[start] % MOD;
int mid = (start + end) / 2;
return tree[node] = (init(node * 2, start, mid) * init(node * 2 + 1, mid + 1, end)) % MOD;
}
static long update(int node, int start, int end, int index, long val) {
if (index < start || index > end) return tree[node];
if (start == end) return tree[node] = val % MOD;
int mid = (start + end) / 2;
return tree[node] = (update(node * 2, start, mid, index, val) *
update(node * 2 + 1, mid + 1, end, index, val)) % MOD;
}
static long query(int node, int start, int end, int left, int right) {
if (right < start || end < left) return 1;
if (left <= start && end <= right) return tree[node];
int mid = (start + end) / 2;
return (query(node * 2, start, mid, left, right) *
query(node * 2 + 1, mid + 1, end, left, right)) % MOD;
}
}
