Machine Learning
머신러닝은 미리 만들어놓은 모델을 활용하여 데이터를 입력하면 스스로 규칙과 패턴을 학습하여 결과를 도출하는 과정을 의미한다.
머신러닝 모델 분석 절차
1. 데이터 전처리 및 탐색
2. 적절한 머신러닝 모델(알고리즘) 선택
3. 머신러닝 모델(알고리즘) 학습
4. 학습한 머신러닝 모델(알고리즘)로 예측 수행
5. 예측 성능 평가
1. 데이터 전처리
1.1. 결측값(Missing Value)
NaN(Not a Number), NA(Not Available) Null 등으로 표현되는 결측값은 미응답, 수집 오류 등으로 인해 입력되어 있어야 할 데이터 값이 비어있는 것을 의미한다. 예컨대 회원가입을 할 때 필수 정보 외에 선택 정보를 입력하는 사람이 있고 입력하지 않는 사람이 있는데, 입력하지 않게 되면 결측값이 발생한다. 그러나 필수 입력 정보가 의미없는 값은 아니기 때문에 결측값이 있다고 하여 단순히 삭제하는 것은 바람직하지 않다. 정보의 손실을 최소화할 수 있는 방향으로 결측값을 처리하는 것이 중요하다.
결측값 처리
1) 완전 제거법(Listwise Deletion)
결측값이 포함된 자료를 제거하는 방법이다. 그러나, 결측값이 일부 있더라도 의미 없는 데이터라고 할 수 없기 때문에 결측값이 포함된 자료를 제거하는 것은 바람직하지 않다. 특히 현실적으로 결측값이 없는 데이터가 더 희소한데 이를 모두 삭제한다면 유의미한 분석을 할 수 없다.
2) 평균 대체법(Mean Value Imputation)
결측값을 해당 Feature 값의 평균으로 대체하는 방법이다. 가장 단순한 방법이나, 추정량의 표준오차가 과소추정되는 문제가 있다. 예컨대 특정 Feature의 값이[9, 15, NA]일 때 평균 대체법은 NA를9와15의 평균인12로 대체한다[9, 15, 12]. 그런데 NA의 실제 값이99였다면 표준오차가 과소 추정되는 것이다.
3) 핫 덱 대체법(Hot Deck Imputation)
결측값이 있는 데이터와 가장 유사한 특성을 가진 다른 데이터의 정보를 이용하여 대체하는 방법이다.
4) 기타
Regression imputation, KNN imputation 등
1.2. 이상값(Outlier)
다른 데이터와 동떨어진 데이터를 의미한다. 이상값은 의미가 있는 값일 수도 있고 의미가 없는 값일 수도 있기 때문에 분석 목표에 따라 적절히 처리해야 한다. 또한 이상값은 단순히 입력 오류일 수도 있다.
이상값 탐지
1) Box Plot
일반적으로 IQR의 값을 기반으로 일정 범위를 설정하여 그 범위를 벗어난 것을 이상값으로 처리한다. 아래서 그림에서 설정한 ±(IQR × 1.5) 값에서 1.5는 조정할 수 있으나 일반적으로 1.5를 사용한다.
- IQR(InterQuartile range)
Q1(25 Percentile) 값과 Q3(75 Percentile) 값의 차이를 의미한다.
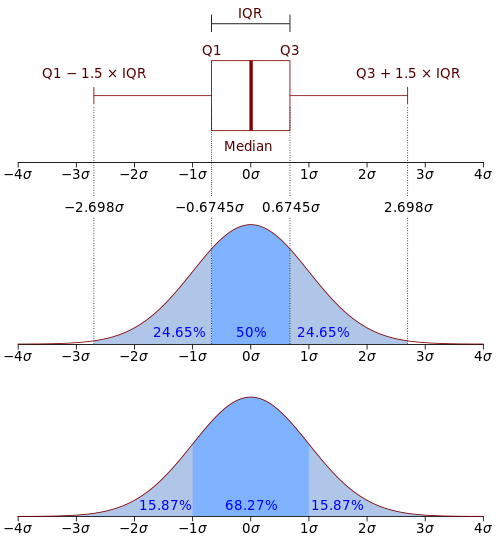
2) Z-score
표준화 점수라고도 하며, 정규분포의 표준편차가 ±2 또는 ±3보다 큰 값을 이상값으로 처리한다. 즉 2𝛔(전체의 2.3%) 또는 3𝛔(0.1%) 값을 이상치로 판단하는 것이다.

이상값 처리
1) 제외(trimming)
이상값을 제외하고 데이터를 분석하는 것이다. 그러나 정보 손실이 발생하기 대문에 분석 목적에 따라 추정량의 왜곡이 발생할 수 있다.
2) 대체(Winsorization)
이상값을 정상값 중 최대값 또는 최소값 등으로 대체하는 방법이다.
3) 변수변환
자료값 전체에 로그변환, 제곱근 변환 등을 적용하는 방법이다.
4) 변수구간화(Binning)
연속형 변수를 구간으로 구분하여 범주화하는 방법이다. 예컨대 소득수준을 10분위로 나누는 것 등의 방법을 의미한다. 이상치 문제를 완화할 수 있고, 결측치를 처리할 수 있기 때문에(값 없음, 결측 범주 등으로 구분) 효과적인 해결 방법이다. 특히 변수가 단순화되기 때문에 과적합을 방지할 수 있다.
1.3. 데이터 변환
정규 분포를 따르게 하거나, 산포도를 비슷하게 하여 비교를 용이하게 한다. 또는 변수 간의 관계를 단순화하여 분석의 용이성을 높이기 위해 사용한다.
1) Square root transform(제곱근 변환)
오른쪽 꼬리가 긴 데이터를 왼쪽으로 모아준다. 최대값이던 810,000이 900이 되기 때문에 편차가 줄어들게 되는 원리와 같다.
2) Power transform(제곱 변환)
왼쪽 꼬리가 긴 데이터를 오른쪽으로 모아준다.
3) Log Transfrom
제곱근 변환보다 더 큰 치우침이 발생한다. 즉 변환된 값의 변화된 크기가 제곱근 변환보다 매우 크다.
4) Exponential Transfrom
제곱 변환보다 더 큰 치우침이 발생한다. 즉 변환된 값의 변화된 크기가 제곱 변환보다 매우 크다.
5) Box-Cox Transfrom
제곱근 유형의 변환과 제곱 유형의 변환을 일반화한 식을 의미한다.
1.4. 데이터 결합
서로 다른 datasets를 결합한다.
| X1 | X2 | + | X1 | X3 |
|---|---|---|---|---|
| A | 1 | A | T | |
| B | 2 | B | F | |
| C | 3 | D | T |
1) Inner Join
key가 공통으로 존재하는 record만 결합한다.
X1 X2 X3 A 1 T B 2 F
2) Full Outer Join
key가 하나라도 존재하는 recode 모두를 결합한다.
X1 X2 X3 A 1 T B 2 F C 3 NA D NA T
3) Left Join
왼쪽 Table에 존재하는 key의 record만 결합한다.
X1 X2 X3 A 1 T B 2 F C 3 NA
3) Right Join
오른쪽 Table에 존재하는 key의 record만 결합한다.
X1 X2 X3 A 1 T B 2 F D NA T
2. 머신러닝 모델 분류
2.1. 지도학습(Supervised Learning)
정답이 있는 데이터를 학습하는 방식이다.
데이터의 값이 연속형이면 회귀(Regression) 알고리즘을 적용하고,
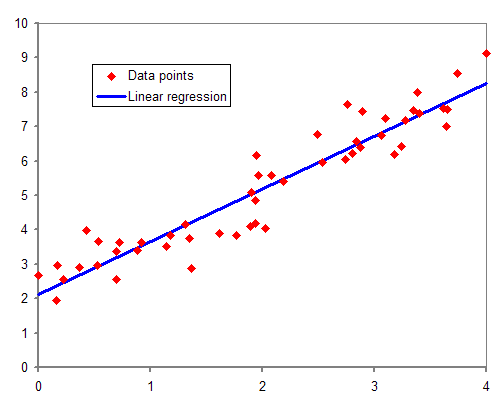
데이터의 값이 범주형이면 분류(Classification) 알고리즘을 적용한다.
대표적인 회귀 알고리즘
- Linear Regression
- k-nearest Neighbors(KNN)
- Logistic Regression
- Softmax Regression
회귀와 분류 모두 가능한 대표적인 알고리즘
- Decision Tree
- SVM
- Random Forest
- Boosting
- Neural Network
- Deep Learning
2.2. 비지도학습(Unsupervised Learning)
정답이 없는 데이터에서 변수들 간의 관계나 유사성을 기반으로 학습하는 방식이다. 자율학습이라고도 불리며, 군집화 (clustering), 차원축소 (dimension reduction), 추천시스템 (recommendation) 등에 활용된다.
1) 군집화 (clustering)
특정 변수의 유사성 또는 차이점을 학습하여 데이터를 일정한 군집으로 분류하는 것을 의미한다.
2) 차원축소 (dimension reduction)
Features의 개수가 너무 많을 때 각 Feature의 특성은 최대한 반영하되, 전체 Features의 개수를 압축시키는 것을 의미한다.
대표적인 차원축소 알고리즘
- PCA
- LDA
- t-SNE
3) 추천시스템 (recommendation)
넷플릭스의 추천 알고리즘과 같이, features 값이 유사한 데이터를 학습하여 추천하는 것을 의미한다.
대표적인 알고리즘
- k-means Clustering
- Hierarchical Clustering
- PCA
- t-SNE
- Apriori
- Auto-Encoders
2.3. 강화학습 (Reinforcement Learning)
비지도학습의 하나로, 행동을 하는 주체(Agent)가 행동(Action)을 수행하면, 환경(Environment)에 의해 상태(State)와 보상(Reward)이 바뀌는데, 이 때 Agent가 Reward를 계속해서 증가시킬 수 있는 방향으로 학습하는 것을 의미하낟.
대표적인 알고리즘
- SARSA
- Q-Learning
3. 머신러닝 모델 학습
과대적합(Overfitting)
학습한 자료에 과도하게 머신러닝 모델이 맞춰져, 다른 자료에 대한 예측력은 떨어지는 것을 의미한다. model complexity이 높은 것을 의미한다. 머신러닝 모델을 학습할 때는 항상 과대적합 문제를 고려해야 한다.
아래 그림에서 초록색 선이 과대적합된 머신러닝 분류 모델을 의미한다. 일반화되지 않고 학습하는 Datasets을 100% 구분할 수 있으나, 새로운 데이터를 예측하면 정확도가 매우 떨어질 수 있다. 따라서 검은색 선 같은 모델을 도출하는 것이 바람직하다.
그렇다고 너무 모델을 일반화(단순화)하게 되면 과소적합(Underfitting)이 발생하기 때문에 적절한 지점을 찾는 것이 관건이다.
과대적합 제한 방법
- 학습 데이터의 크기를 크게함
- 차원 축소, 파라미터에 규제(regularization)를 적용하여 Model complexity(모델의 복잡도)를 낮춤

4. 머신러닝 모델의 검증 및 평가
과대적합의 문제를 방지하고 일반화 오차를 줄이기 위해서 새로운 데이터의 예측 성능을 평가해야 한다. 따라서 모델을 학습할 때 사용하지 않은 데이터를 가지고 검증 및 평가를 수행해야 한다. 만약 모델을 학습할 때 사용한 데이터를 바탕으로 검증 및 평가를 수행하게 되면 수치가 좋게 나올 수 밖에 없다.
4.1. 데이터 분할
Hold-out
datasets을 두 개 또는 세 개의 그룹으로 랜덤하게 분할하는 방식을 의미한다.
1) Training Data
머신러닝 모델의 학습을 위해 사용하는 데이터를 의미한다. 전체 datasets 중에서 가장 큰 비율을 할당한다.
2) Validation Data
머신러닝 모델을 학습하는 과정에서 최적 성능으로 튜닝하기 위해 사용하는 데이터를 의미한다. Hyperparameter를 조정하거나 Model selecting(변수 선택)등에 활용한다.
3) Test Data
머신러닝 모델의 성능을 평가할 때 사용하는 데이터를 의미한다. 일반적으로 Training Data를 사용해 도출된 성능 수치보다, Test Data를 사용해 도출된 성능이 낮다. 이 차이가 큰 경우를 과대적합이라고 한다.
K-fold Cross-validation(교차 검증)
일반적으로 자료의 수가 충분하지 않은 경우에 사용한다. 자료를 균등하게 개의 그룹으로 분할한 후 데이터 중 하나만 Test 데이터로 사용하는 방식이다. 따라서 번 만큼 학습을 반복한다. 학습을 번 반복하면 개의 성능 수치가 나오는데 이 수치를 평균한 값을 K-fold 모델의 성능으로 평가한다.
계산양이 많기 때문에 훈련 시간이 많이 걸린다는 단점이 있으나, 더 많은 데이터를 활용할 수 있다는 장점이 존재한다.
일반적으로 5 이상의 k값을 사용한다.
예컨대 k=3이면 아래 그림과 같다.
| Train | Test |
|---|---|

편향-분산 트레이드 오프(Bias-Variance Trade off)
-
Bias
예측 모델과 실제 값의 차이의 정도를 의미한다. -
Variance
새로운 학습 데이터를 넣을 때 마다 달라지는 예측 모델의 정도를 의미한다.
4.2. 지도학습 모델 평가 지표
회귀 모델 평가 지표
예측값과 실제값의 오차를 통해 학습한 모델의 성능을 평가한다.
1) RMSE (Root mean square error)
오차의 평균을 의미한다.
- : 실제값
- : 예측값
2) R-square(결정계수)
선형회귀 모델에서 0~1 사이의 값을 가진다. 예측값과 실제값이 모두 일치하면 1로 표현하며 예측값과 실제값이 모두 다르면 0이다. 따라서 R-square 값이 1에 가까울수록 좋다.
3) MAE(mean absolute error)
오차의 평균을 의미한다. RMSE가 제곱을 한 후 제곱근을 취하는 반면 MAE는 절대값의 평균이다.
4) MAPE(mean average percentage error)
실제값에 비해 오차가 차지하는 비중이 평균적으로 얼마인지를 의미한다. 따라서 작을 수록 좋다.
분류 모델 평가 지표
1) confusion matrix(교차 분류표, 정오 분류표)
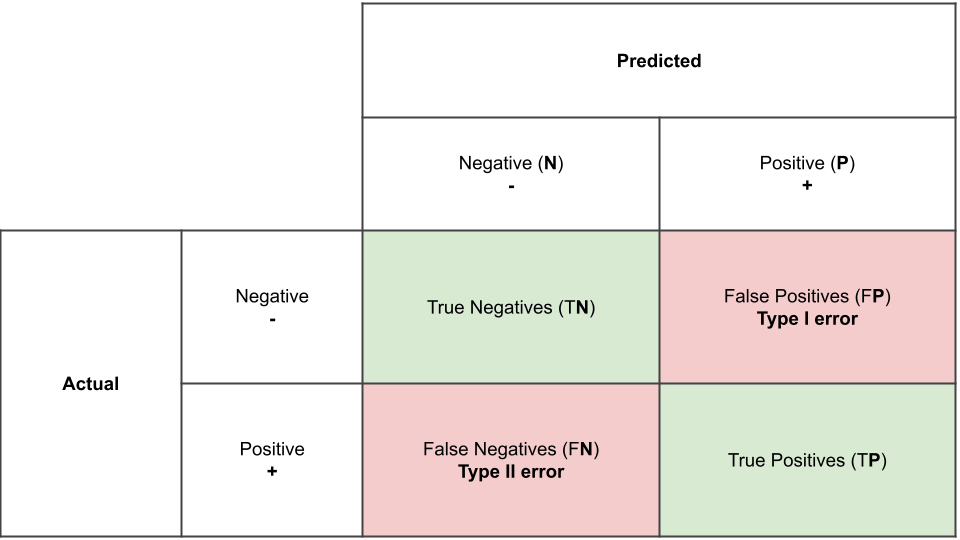
- Type I error
귀무가설(null hypothesis, H0)이 참임에도 기각한 것을 의미한다. 즉 예측하려던 목표의 실제 값이 Positive임에도 Negative로 예측한 것이다.
예컨대 암 환자를 분류하는 모델이라고 할 때, 암 환자가 아닌데도 암 이라고 예측하는 것이다.
- Type II error
귀무가설(null hypothesis, H0)이 거짓임에도 기각하지 않은 것을 의미한다. 즉 예측하려던 목표의 실제 값이 Negative임에도 Positive로 예측한 것이다.
예컨대 실제로는 암 환자이나, 암이 아니라고 예측한 것이다. 그렇기 때문에 일반적으로 암 환자가 아님에도 암이라고 예측했던 Type I error보다, 당장 치료가 필요한 암 환자를 암이 아니라고 예측한 Type II error가 더 큰 비용을 유발한다.
1-1) Accuracy(정확도)
전체 중에서 정확히 예측한 값의 비율을 의미한다. 그러나 정확도만으로 예측 모델의 성능을 측정하는 것은 불완전한 경우가 많다. 특히 Negative와 Positive가 한 쪽으로 치우쳐져 있는(Unbalance) 경우 정확도 지표의 한계가 드러난다. 예컨데 Positive 값의 비율이 전체에서 0.1%인 경우 모든 값을 Negative로 예측하는 단순한 알고리즘의 정확도는 99.9%다.
1-2) Precision(정밀도)
Positive로 예측한 것 중 실제 Positive로 예측한 값의 비율을 의미한다. 따라서 FP가 작을수록 정밀도의 값이 증가한다. Type I error를 줄이는 것이 목표다.
예컨대 스팸메일을 분류하는 경우 스팸메일이 아님(Negative)에도 스팸메일이 맞다(Positive)로 예측하는 경우 중요한 메일을 읽지 못할 수 있다. 이럴 때는 정밀도가 중요한 성능 평가 지표가 된다.
1-3) Recall(재현율)
실제 Positive인 값 중에서 Positive로 예측한 값의 비율을 의미한다. Type II error를 줄이는 것이 목표다.
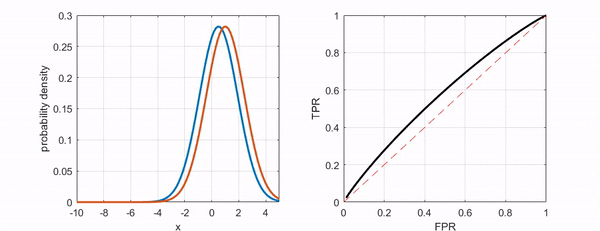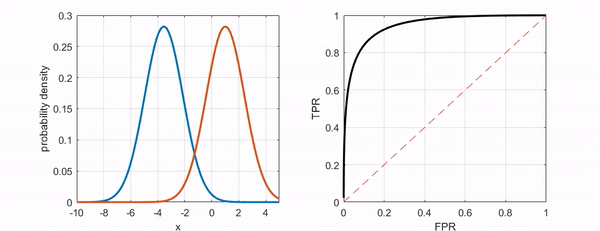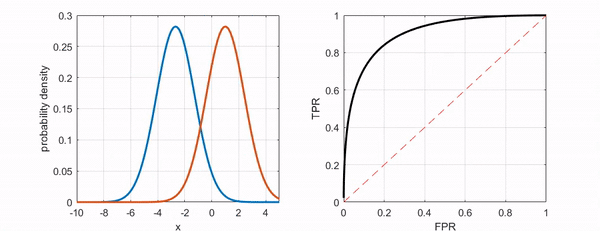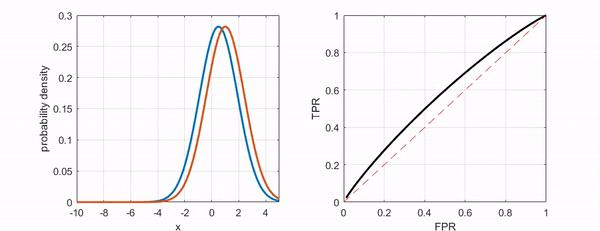
2) ROC(Receiver Operating Characteristic)
분류의 결정임계값(threshold)에 따라 달라지는 TPR(민감도, sensitivity)과 FPR(1-specificity)의 조합을 의미한다.
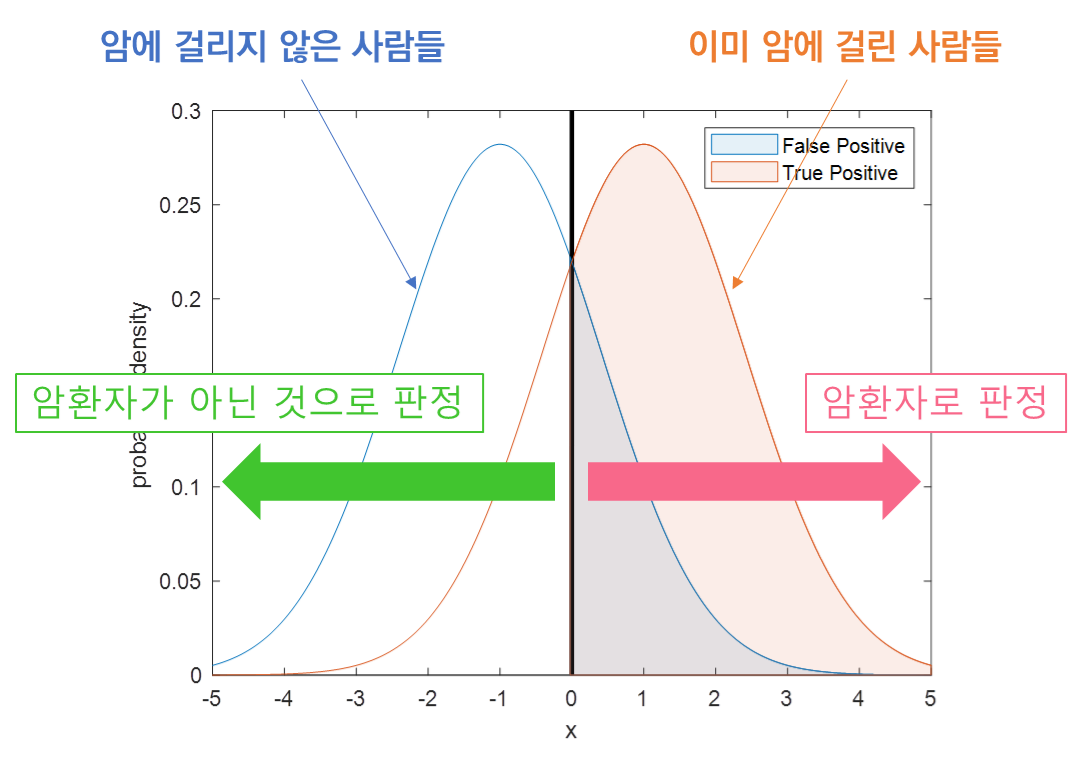
- Threshold
예측값을 판단하는 기준을 의미한다. 예컨대 Positive일 확률이 90% 이상일 때만 Positive로 예측한다면 Threshold는 0.9다.
- TPR(True Positive Rate)
Sensitivity(민감도)를 의미한다. Positive를 Positive로 예측한 비율이다.
- FPR(False Positive Rate)
1-specificity(특이도)를 의미한다. Negative를 Positive로 예측한 비율이다.
[참고 자료] 공돌이의 수학정리노트 - ROC curve
3) AUC(Area Under the Curve)
ROC Curve의 아래 면적을 의미한다. 1에 가까울수록 좋다.