평가지표(Evaluation Metrics)는 머신러닝 및 통계 모델의 성능을 평가하는 데 사용되는 다양한 측정 기준입니다. 모델이 예측한 값과 실제 값 간의 차이를 정량적으로 측정하여 모델의 정확성을 평가하고, 모델 간의 비교 및 선택에 도움을 줍니다. 주요 평가지표와 그 용도는 다음과 같습니다
주요 평가지표
-
ME (Mean Error)
- 정의: 실제 값과 예측 값의 차이의 평균.
- 사용처: 예측값이 실제값보다 얼마나 높은지 또는 낮은지를 확인.
- 장점: 간단하고 직관적.
- 단점: 양의 오차와 음의 오차가 상쇄되어 실제 오차의 크기를 왜곡할 수 있음.
-
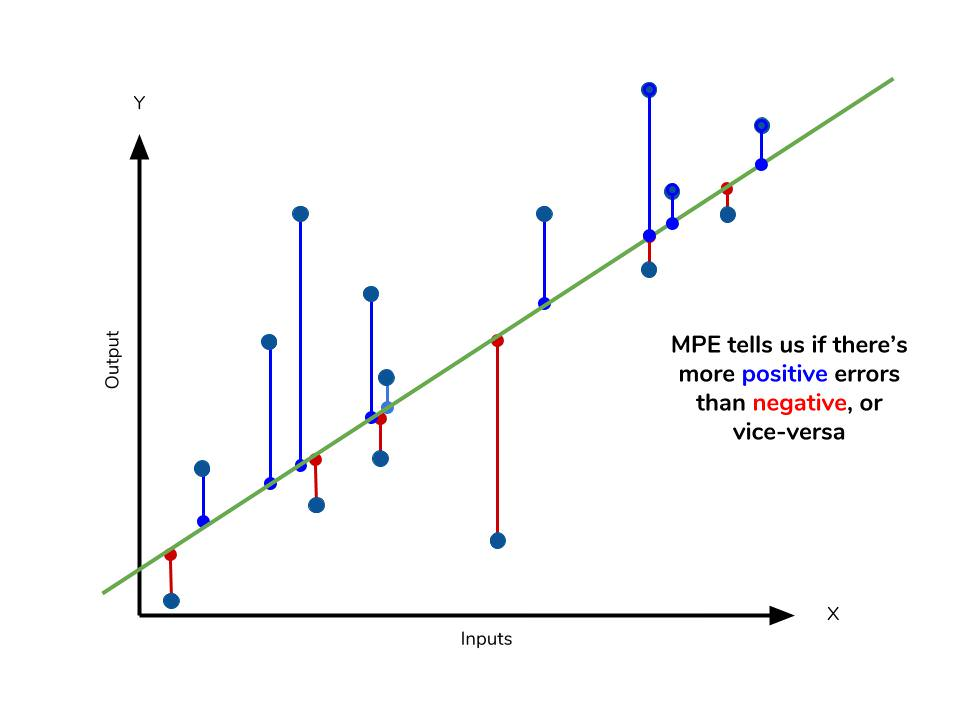
MPE (Mean Percentage Error)
- 정의: 예측 오차를 실제 값의 백분율로 나타낸 값의 평균.
- 사용처: 예측 오차를 백분율로 나타내어 상대적인 오차 크기를 파악.
- 장점: 상대적인 오차를 이해하기 쉬움.
- 단점: 실제 값이 0에 가까울 때 불안정.
-
SMAPE (Symmetric Mean Absolute Percentage Error)
- 정의: 예측 오차를 실제 값과 예측 값의 절대 값 평균의 백분율로 나타낸 값.
- 사용처: 예측 오차를 대칭적으로 처리하여 모델 성능을 평가.
- 장점: 0에 가까운 값도 잘 처리.
- 단점: 계산이 다소 복잡할 수 있음.
-
RMSE (Root Mean Squared Error)
- 정의: 예측 값과 실제 값 간의 차이의 제곱 평균의 제곱근.
- 사용처: 모델의 예측 정확도를 평가.
- 장점: 큰 오차에 민감하여 모델 성능을 엄격히 평가.
- 단점: 이상치에 의해 왜곡될 수 있음.
-
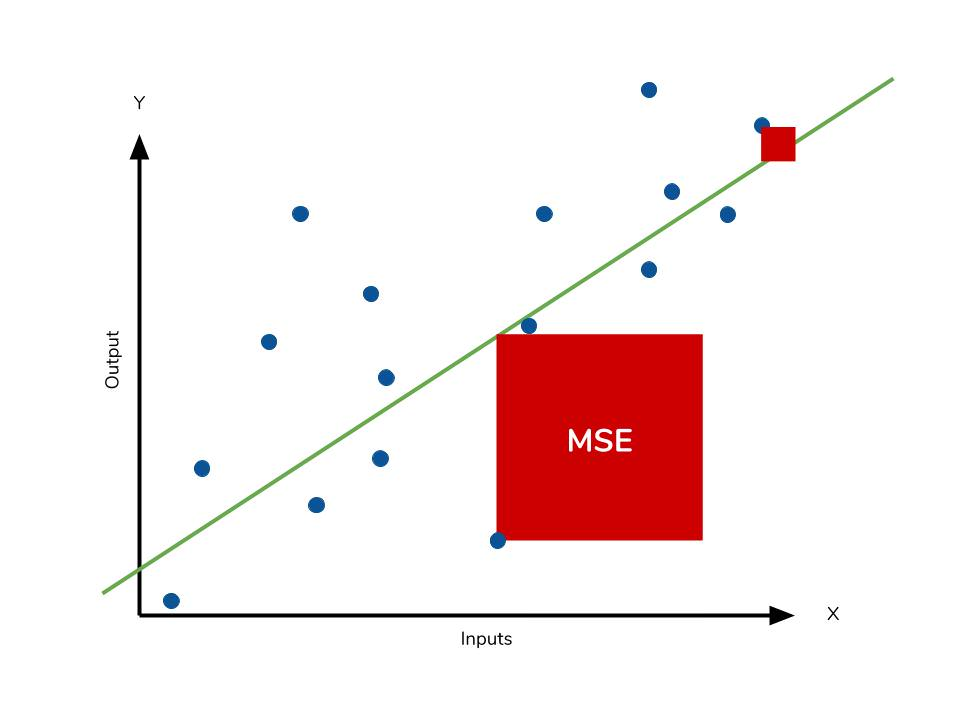
MSE (Mean Squared Error)
- 정의: 예측 값과 실제 값 간의 차이의 제곱 평균.
- 사용처: 모델의 예측 정확도를 평가.
- 장점: 계산이 간단하고 직관적.
- 단점: 큰 오차에 민감하여 이상치에 의해 왜곡될 수 있음.
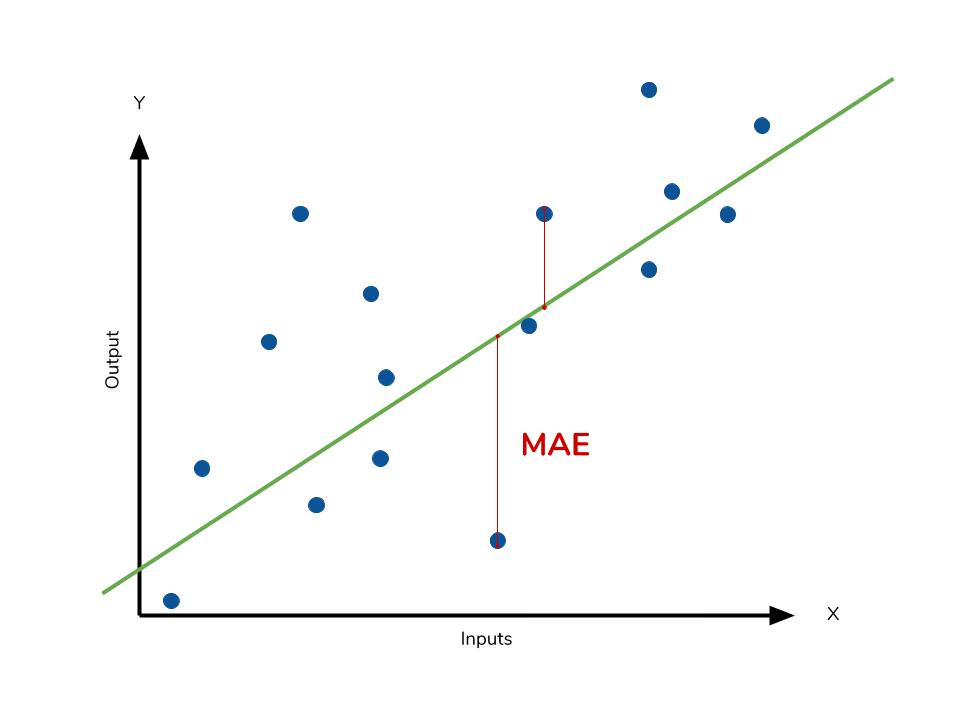
- MAE (Mean Absolute Error)
- 정의: 예측 값과 실제 값 간의 절대 오차의 평균.
- 사용처: 오차의 방향성을 제거하고 오차의 크기만을 평가.
- 장점: 계산이 간단하고 양의 오차와 음의 오차가 상쇄되지 않음.
- 단점: 큰 오차에 민감하지 않음.
- R-squared (R²)
- 정의: 모델의 설명력을 나타내며, 예측 값이 실제 값을 얼마나 잘 설명하는지를 평가.
- 사용처: 모델의 설명력을 직관적으로 평가.
- 장점: 모델이 데이터를 얼마나 잘 설명하는지 쉽게 이해.
- 단점: 복잡한 모델의 경우 과적합의 위험이 있음.
용도
- 모델 평가: 학습된 모델의 성능을 정량적으로 평가하여, 모델이 실제 데이터를 얼마나 잘 예측하는지 파악.
- 모델 비교: 여러 모델 간의 성능을 비교하여 최적의 모델을 선택.
- 모델 개선: 평가지표를 통해 모델의 약점을 발견하고, 이를 바탕으로 모델을 개선.
- 의사결정 지원: 비즈니스나 연구에서 모델의 예측 성능을 바탕으로 한 의사결정을 지원.
평가지표는 모델의 성능을 평가하고 개선하는 데 필수적인 도구입니다. 이를 통해 모델의 강점과 약점을 파악하고, 보다 정확한 예측을 수행할 수 있습니다.

1. 평가지표 설명
ME (Mean Error)
Mean Error (ME)는 예측값과 실제값 사이의 차이의 평균을 나타냅니다. 이 지표는 예측값이 실제값보다 얼마나 높은지 또는 낮은지를 보여줍니다.
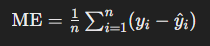
MPE (Mean Percentage Error)
Mean Percentage Error (MPE)는 예측 오차를 실제값의 백분율로 나타내며, 예측값과 실제값 사이의 차이의 평균 백분율을 보여줍니다.
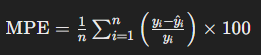
SMAPE (Symmetric Mean Absolute Percentage Error)
SMAPE는 예측 오차를 실제값과 예측값의 절대값 평균의 백분율로 나타내며, 예측값과 실제값 사이의 대칭적인 평균 절대 백분율 오차를 보여줍니다.
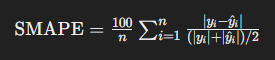
RMSE (Root Mean Squared Error)
Root Mean Squared Error (RMSE)는 예측값과 실제값 사이의 차이의 제곱의 평균을 구한 후, 그 제곱근을 취한 값입니다. 이는 오차의 크기를 강조하는 효과가 있습니다.
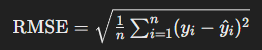
MSE (Mean Squared Error)
Mean Squared Error (MSE)는 예측값과 실제값 사이의 차이의 제곱의 평균을 나타냅니다. 이는 오차의 크기를 강조하는 효과가 있습니다.
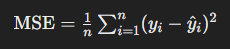
2. 각각의 장단점
ME
- 장점: 간단하고 직관적입니다.
- 단점: 양의 오차와 음의 오차가 서로 상쇄될 수 있어 오차의 크기를 왜곡할 수 있습니다.
MPE
- 장점: 예측 오차를 백분율로 나타내어 상대적인 오차 크기를 이해하기 쉽습니다.
- 단점: 실제값이 0에 가까울 때 불안정해질 수 있습니다.
SMAPE
- 장점: 예측 오차를 백분율로 나타내면서 대칭적으로 처리하여 실제값과 예측값이 0인 경우를 고려합니다.
- 단점: 계산이 다소 복잡하며, 일부 상황에서는 과대평가될 수 있습니다.
RMSE
- 장점: 큰 오차에 대해 민감하며, 모델의 성능을 엄격히 평가합니다.
- 단점: 큰 오차에 너무 민감하여 이상치에 의해 왜곡될 수 있습니다.
MSE
- 장점: 계산이 간단하고 직관적입니다.
- 단점: RMSE와 마찬가지로 큰 오차에 민감하며, 이상치에 의해 왜곡될 수 있습니다.
3. 비교 차이점
- ME vs. MPE: ME는 절대 오차를 측정하는 반면, MPE는 오차를 백분율로 측정합니다.
- MSE vs. RMSE: MSE는 오차의 제곱 평균을 계산하며, RMSE는 그 제곱근을 취합니다. RMSE는 MSE보다 오차의 크기에 더 민감합니다.
- SMAPE vs. MPE: SMAPE는 예측 오차를 대칭적으로 처리하며, 백분율로 나타내어 실제값과 예측값이 0인 경우를 고려합니다. MPE는 예측 오차를 실제값의 백분율로 나타냅니다.
4. 다른 평가지표
MAE (Mean Absolute Error)
Mean Absolute Error (MAE)는 예측값과 실제값 사이의 절대 오차의 평균을 나타냅니다. 이는 오차의 방향성을 제거하고, 오차의 크기만을 평가합니다.
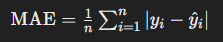
- 장점: 계산이 간단하고, 양의 오차와 음의 오차가 상쇄되지 않습니다.
- 단점: 큰 오차에 대해 민감하지 않으며, MSE나 RMSE에 비해 이상치에 덜 민감합니다.
R-squared (R²)
R-squared는 모델의 설명력을 나타내는 지표로, 예측값이 실제값을 얼마나 잘 설명하는지를 평가합니다. 1에 가까울수록 모델이 데이터를 잘 설명한다는 것을 의미합니다.
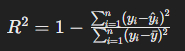
- 장점: 모델의 설명력을 직관적으로 이해할 수 있습니다.
- 단점: 복잡한 모델의 경우, 과적합의 위험이 있습니다.
이러한 평가지표들을 잘 이해하고 적절히 사용하면, 모델의 성능을 더 정확히 평가하고 개선할 수 있습니다.
GPT 설명과 자료 참고
https://www.dataquest.io/blog/understanding-regression-error-metrics/