🧸알고리즘
다른 분의 블로그를 보고 정리한 글입니다.
https://dev-coco.tistory.com/160
🍀DP
동적 계획법(DP, Dynamic Programming)에 대해 설명해주세요.
주어진 문제를 풀기 위해, 문제를 여러 개의 하위문제로 나누어 푸는 방법을 말합니다.
동적 계획법에서는 어떤 부분 문제가 다른 문제들을 해결하는데 사용될 수 있어, 답을 여러 번 계산하는 대신 한번만 계산하고
그 결과를 재활용하는 메모이제이션(Memoization)기법으로 속도를 향상시킬 수 있습니다.
메모이제이션: 동일한 계산을 반복 수행 할 때, 이전의 계산한 값을 재사용함으로써 동일한 계산 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술
동적 계획법(DP, Dynamic Programming)이 갖는 2가지 조건은 무엇인가요?
-
중복되는 부분(작은) 문제
중복되는 부분 문제는 나눠진 부분 문제가 중복되는 경우로, 메모이제이션 기법을 통해 중복 계산을 없앱니다. -
최적 부분 구조
최적 부분 구조를 가진다는 것은 전체 문제의 최적해가 부분 문제의 최적해들로써 구성된다는 것입니다.
🍀 Sorting Algorithm
버블 정렬(Bubble Sort)에 대해 설명해주세요.
버블 정렬은 서로 인접한 두 원소를 비교해서 정렬하는 알고리즘입니다. 시간복잡도는 O(n^2) 입니다.
선택 정렬(Selection Sort)에 대해 설명해주세요.
선택 정렬은 첫 번째 값을 두 번째 값부터 마지막 값까지 차례대로 비교하여 최솟값을 찾아 첫 번째에 놓고, 두 번째 값을 세번째 값부터 마지막 값까지 비교해 최솟값을 찾아 두번째 위치에 놓는 과정을 반복해 정렬하는 알고리즘입니다. 시간복잡도는 O(n^2)입니다.
삽입 정렬(Insertion Sort)에 대해 설명해주세요.
삽입 정렬은 두번째 값부터 시작해 그 앞에 존재하는 원소들과 비교해서 삽입할 위치를 찾아 삽입하는 정렬 알고리즘입니다. 평균 시간복잡도는 O(n^2)이며, BestCase의 경우 O(n)까지 높아질 수 있습니다.
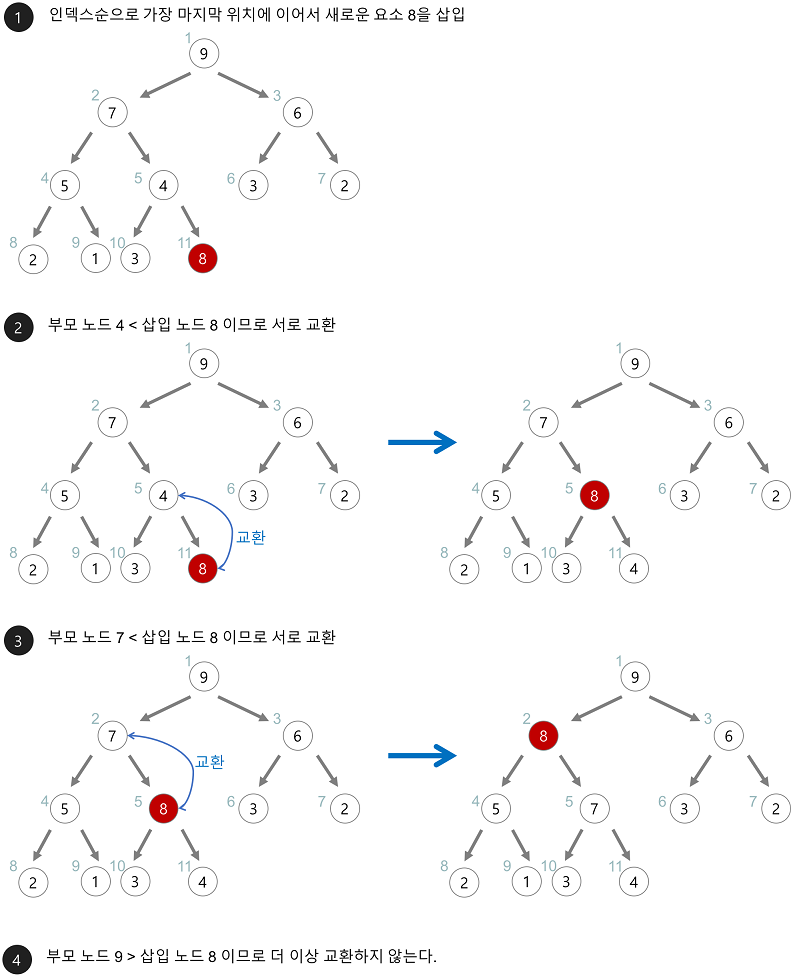
힙 정렬(Heap Sort)에 대해 설명해주세요.
힙 정렬은 주어진 데이터를 힙 자료구조로 만들어 최댓값 또는 최솟값부터 하나씩 꺼내서 정렬하는 알고리즘 입니다. 시간 복잡도는 O(nlogn)입니다.
병합 정렬(Merge Sort)에 대해 설명해주세요.
병합 정렬은 주어진 배열을 크기가 1인 배열로 분할하고 합병하면서 정렬을 진행하는 분할/정복 알고리즘입니다. 시간 복잡도는 O(nlogn)입니다.
퀵 정렬(Quick Sort)에 대해 설명해주세요.
퀵 정렬은 빠른 정렬 속도를 자랑하는 분할/정복 알고리즘 중 하나로 피봇을 설정하고 피봇보다 큰 값과 작은 값으로 분할해 정렬합니다. 병합 정렬과 다르게 리스트를 비균등하게 분할합니다.
시간 복잡도는 O(nlogn)이며 worst case의 경우 O(n^2)까지 나빠질 수 있습니다.
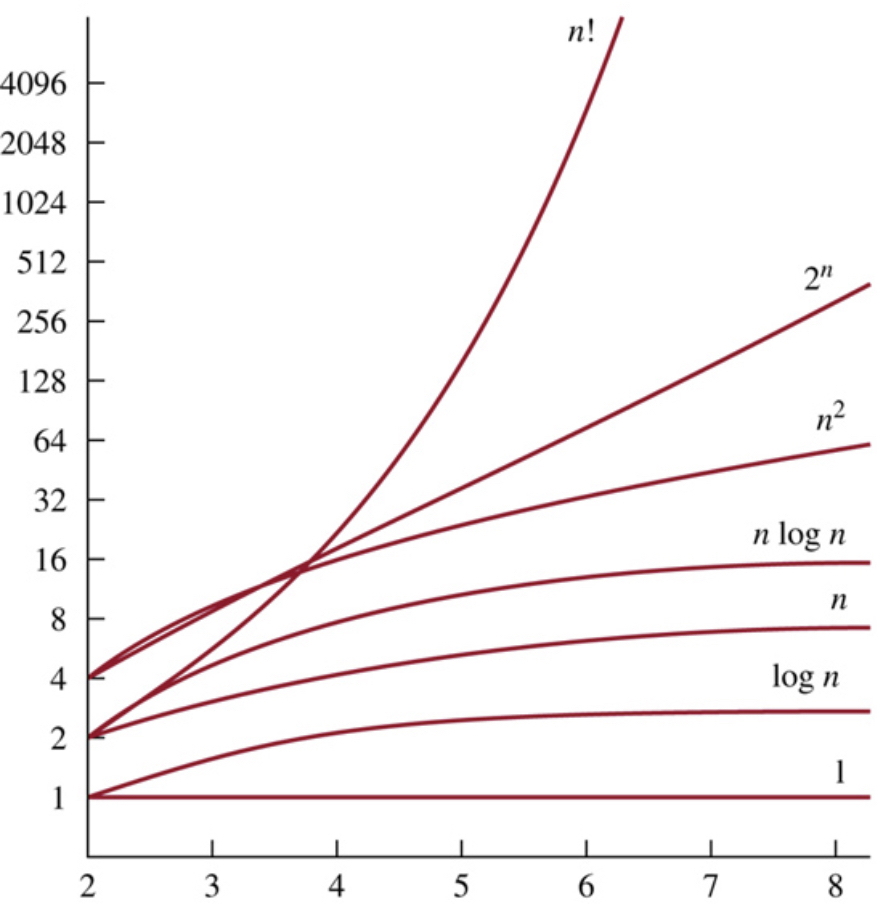
Big-O 표기법의 시간 복잡도 크기 순서를 말해주세요.
O(1) < O(log n) < O(n) < O(nlog n) < O(n^2) < O(2^n) < O(n!)
허프만 코딩에 대해 설명해주세요.
허프만 코딩은 문자의 빈도수를 가지고 압축하는 과정을 말하며, 접두부 코드와 최적 코드를 사용합니다.
- 접두부 코드
각 문자에 부여된 이진 코드가 다른 이진 코드의 접두부가 되지 않는 코드 - 최적 코드
인코딩된 메시지의 길이가 가장 짧은 코드
재귀 알고리즘에 대해 설명해주세요.
재귀 알고리즘이란 함수 내부에서 함수가 자기 자신을 호출하여 문제를 해결하는 알고리즘입니다.
자기 자신을 계속해서 호출해서 끝없이 반복하게 되므로 반복을 중단할 조건이 반드시 필요합니다.
피보나치 수열의 N번째 값을 구하는 메소드에 대해 각각 재귀와 반복문으로 손코딩(또는 수도코딩) 해주세요.
#반복문
n = int(input())
dp = [0,1]
for i in range(2,n+1):
dp.append(dp[i-1]+dp[i-2])
print(dp[n])
#재귀
n = int(input())
def fib(x):
if x==0:
return 0
elif x==1:
return 1
else:
return fib(x-1)+fib(x-2)
print(fib(n))팩토리얼의 N번째 값을 구하는 메소드에 대해 각각 재귀와 반복문으로 손코딩(또는 수도코딩) 해주세요.
#반복문
n = int(input())
dp = [1,1]
for i in range(2,n+1):
dp.append(dp[i-1]*i)
print(dp[n])
#재귀
n = int(input())
def fac(x):
if x==1:
return 1
else:
return fac(x-1)*x
print(fac(n))