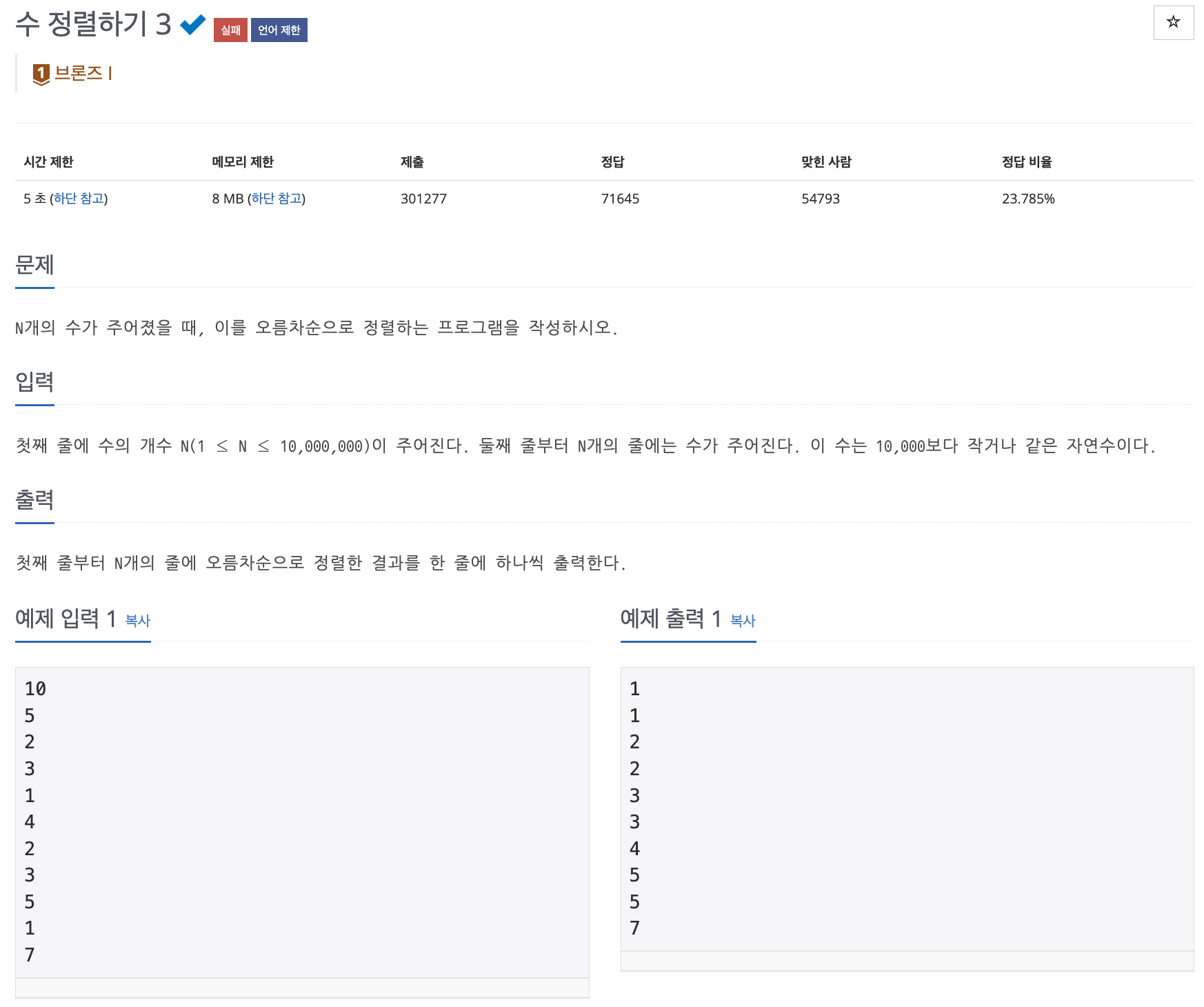
📌 문제 : 백준 10989번
📌 문제 탐색하기
N : 정수의 개수 (1 ≤ N ≤ 10,000,000)
nums : N개의 정수 (1 ≤ num ≤ 10,000)
✅ 입력 조건
1. N 입력
2. N개의 정수를 N번 반복해 입력
✅ 출력 조건
1. 정렬된 정수를 하나씩 출력
sort() 함수로 정렬하거나 for문 내에서 append로 리스트에 값을 추가하는 식의 코드는 메모리 초과를 발생시킨다.
대신, 미리 10001 크기의 리스트를 정의한다.
N개의 정수를 돌면서 해당 정수를 그 리스트의 인덱스로 접근하여 값을 올려준다.
이 값은 중복된 숫자의 개수를 의미하게 된다.
그 후, 10001 크기의 리스트를 돌면서 해당 값만큼 인덱스 값을 반복해 출력해주면 원하는 방식으로 구현할 수 있다.
→ 위와 같은 방식은 카운팅 정렬(계수 정렬) 알고리즘을 기반으로 하였다.
가능한 시간복잡도
N개의 정수를 리스트의 인덱스로 접근해 개수 세기 →
리스트 접근해 그 개수만큼 인덱스 출력 →
최종 시간복잡도
으로 제한 시간 내에 연산이 가능하다.
알고리즘 선택
정수를 인덱스로 접근해 개수 세고 그 리스트를 돌면서 인덱스 출력하기.
📌 코드 설계하기
- N 입력
- N개의 자연수 입력
- 10001 크기의 리스트 정의
- N개의 정수를 리스트의 인덱스로 접근하여 개수 세기
- 리스트에 접근해 그 개수만큼 인덱스 출력
📌 시도 회차 수정 사항
1회차
import sys
input = sys.stdin.readline
# N 입력
N = int(input())
# N개의 수 입력
nums = [int(input()) for _ in range(N)]
# 오름차순 정렬
nums.sort()
# 원하는 형식으로 출력
for num in nums:
print(num)- 결과

- 가장 기본적인
sort()로 정렬하는 방식으로 풀었더니 메모리 초과가 발생했다. - 1 ≤
N≤ 10,000,000이라는 범위 때문에sort()를 이용한 정렬 방식은 적합하지 않았다. - 전체 시간 복잡도 :
2회차
import sys
import heapq
input = sys.stdin.readline
# N 입력
N = int(input())
# N개의 수 입력
nums = [int(input()) for _ in range(N)]
# 최소 힙 사용
heapq.heapify(nums)
# 오름차순 정렬해 저장할 리스트 정의
result = []
# heapq.heappop을 반복하여 최소값 추출하며 정렬
for _ in range(N):
result.append(str(heapq.heappop(nums)))
# 원하는 형식으로 출력
for i in result:
print(i)- 결과

- 메모리 사용량을 줄이기 위해 heap을 활용한 힙 정렬을 이용하였다.
- 하지만 똑같이 메모리 초과가 발생했다.
- for문 내에서 append를 사용하면 메모리 재할당이 발생해 메모리를 효율적으로 사용할 수 없다고 한다.
- 전체 시간 복잡도 :
3회차
import sys
input = sys.stdin.readline
# 1. N 입력
N = int(input())
# 2. N개의 자연수 입력
nums = [int(input()) for _ in range(N)]
# 3. 10001 크기의 리스트 정의
count = [0] * 10001
# 4. N개의 정수를 리스트의 인덱스로 접근하여 개수 세기
for num in nums:
count[num] += 1
# 5. 리스트에 접근해 그 개수만큼 인덱스 출력]
for i in range(10001):
# count[i]이 1 이상이라면
if count[i] != 0:
# 그 값만큼 출력
for j in range(count[i]):
print(i)- 결과

- 입력 한번에 받아서 리스트에 저장했더니 입력 개수가 굉장히 큰 경우에 메모리 초과가 발생했다.
- 입력을 받을 때마다 처리하는 방식으로 변경해야 했다.
📌 정답 코드
import sys
input = sys.stdin.readline
# 1. N 입력
N = int(input())
# 2. 10001 크기의 리스트 정의
count = [0] * 10001
# 3. N개의 정수를 리스트의 인덱스로 접근하여 개수 세기
for _ in range(N):
num = int(input())
count[num] += 1
# 4. 리스트에 접근해 그 개수만큼 인덱스 출력
for i in range(10001):
# count[i]이 1 이상이라면
if count[i] != 0:
# 그 값만큼 출력
for j in range(count[i]):
print(i)- 결과

📌 회고
- 여러 정렬 방식을 잘 익히고 있어야 한다는 것을 제대로 느낄 수 있는 문제였다.
- 시간 초과 외의 메모리를 신경써야 하는 문제는 처음 풀었는데, 문제를 풀 때 자주 사용했던 함수들이 메모리에 이렇게 영향을 주는지 몰랐다.
- 파이썬 함수의 메모리 관련한 특징들을 공부해놓아야겠다.
📌 기억할 정보
정렬 알고리즘 종류
1️⃣ 버블 정렬 (Bubble Sort)
💡 기본 원리
- 인접 원소들을 비교, 필요에 따라 위치 교환하는 방식
- 큰 값(or 작은 값)이 배열 통해 버블(거품)처럼 서서히 상단(or 하단)으로 이동
💡 작동 원리
- 배열의 각 원소 순회 → 인접 원소 비교 → 필요 시 위치 교환 → 최종 정렬
💡 특징
- 이해 & 구현 쉬움
- 시간 복잡도 : 최악 & 최선 모두
- 공간 복잡도 : → 제자리 정렬(
In-place sorting) - 안정성 : 안정 정렬
- 효율성 : 대규모 데이터 셋에선 비효율적
💡 구현
# 버블 정렬
def bubble_sort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
return arr
# 정렬 조기 종료 최적화한 버블 정렬
def optimized_bubble_sort(arr):
n = len(arr)
for i in range(n):
swapped = False
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
swapped = True
if not swapped:
break2️⃣ 선택 정렬 (Selection Sort)
💡 기본 원리
- 배열/리스트 정렬하는 간단 비교 기반 알고리즘
- 전체 배열 순회 → 각 위치에 올바른 값 찾아 배치 ➡️ 모든 요소 정렬될 때까지 반복
💡 작동 원리
- 최소값 탐색 : 배열 전체에서 최소값 탐색
- 스왑(
swap) : 최소값을 배열 현재 위치와 교체, 처음엔 배열 첫번째 위치에서 시작 - 다음 위치로 이동 : 남은 배열에 대해 최소값 다시 탐색
- 반복 : 모든 요소 정렬될 때까지 반복
💡 특징
- 스왑 횟수 : 비교 횟수에 비해 교환(
swap) 횟수 적음 → 최악n-1번 - 시간 복잡도 : 배열 크기
n일 때, 약n(n-1)/2번 비교 → - 공간 복잡도 : → 제자리 정렬(
In-place sorting)- 추가적인 메모리 공간 거의 사용 ❌
- 안정성 : 불안정 정렬
- 효율성 : 대규모 데이터 셋에선 비효율적
💡 구현
def selection_sort(arr):
n = len(arr)
# 각 반복마다 가장 작은 요소 찾아 현재 위치 요소와 교환
for i in range(n):
min_idx = i
for j in range(i+1, n):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
return arr 3️⃣ 삽입 정렬 (Insertion Sort)
💡 기본 원리
- 각 반복에서 하나의 데이터를 적절한 위치에 삽입해 작업 수행
- 이미 정렬 ⭕️/ 정렬 ❌ 부분으로 배열 나눔 → 정렬 ❌ 부분의 각 요소를 정렬된 부분의 적절 위치에 삽입
💡 작동 원리
- 배열 2번째 요소 부터 시작해 정렬 ⭕️ 배열 부분에서 적절한 위치 찾음
- 선택된 요소를 그보다 큰 모든 요소 뒤로 이동 → 적절 위치 삽입
- 배열 모든 요소가 이 과정으로 정렬될 때까지 반복
💡 특징
- 시간 복잡도 : 최선 , 평균 및 최악
- 공간 복잡도 : 의 추가 메모리만 사용
- 안정성 : 안정 정렬
- 효율성 : 작은 데이터셋 또는 거의 정렬된 배열 정렬 시 효율적
- 데이터 양 10만, 100만 개 이상이면 비효율적
💡 구현
def insertion_sort(arr):
for i in range(i, len(arr)):
key = arr[i]
j = i - 1
while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key4️⃣ 퀵 정렬 (Quick Sort)
💡 기본 원리
- 매우 빠른 실행 시간 가지는 비교 기반 정렬 알고리즘
- 분할 정복(divide and conquer) 방식 → 큰 문제를 작은 문제로 나누어 해결
- ❗️핵심
- 피벗(
pivot) 선택- 어떻게 선택하느냐가 효율성에 큰 영향
- 피벗 기준으로 작은 모든 요소는 피벗 왼쪽, 큰 모든 요소는 피벗 오른쪽 위치하도록 배열 재배치
- 분할
- 배열 요소들이 피벗 중심으로 왼쪽/오른쪽 재배치
- 재귀적 접근
- 재귀 깊이 깊어질수록, 처리해야 할 데이터 감소
- 효율적 처리 가능
- 피벗(
💡 작동 원리
- 피벗 선택 : 첫번째, 마지막, 중간 또는 무작위 선택 가능
- 분할 : 선택 피벗 기준 두 부분으로 나눔
- 작은 모든 요소 왼쪽, 큰 모든 요소 오른쪽
- 정복 : 피벗 제외 왼쪽 부분, 오른쪽 부분 각각 재귀적으로 위 과정 반복
- 결합 : 분할 시 요소들 이미 정렬 → 별도 결합 필요 ❌
💡 특징
- 시간 복잡도 : 평균 (피벗 균등 분할 시), 최악 (피벗 최댓값/최솟값 선택 시)
- 공간 복잡도 : In-place 정렬
- 안정성 : 불안정 정렬
| 장점 | 단점 |
|---|---|
| 평균 으로 매우 빠른 실행 시간 | 최악 까지 증가 가능(피벗 선택 불균형일 경우) |
| in-place 정렬 → 추가적 메모리 거의 사용 ❌ | 불안정 정렬 |
| 대규모 데이터셋에 효율적 작동, 실 상황에서 자주 사용 |
💡 구현
def quichSort(arr):
if len(arr) <= 1:
return arr
# pivot 선택
pivot = arr[len(arr) // 2]
# pivot보다 작은 것 왼쪽
left = [x for x in arr if x < pivot]
# 중간값
middle = [x for x in arr if x == pivot]
# pivot보다 큰 것 오른쪽
right = [x for x in arr if x > pivot]
# 재귀적 접근
return quichSort(left) + middle + quickSort(right)5️⃣ 병합 정렬 (Merge Sort)
💡 기본 원리
- 분할 정복(divide and conquer) 방식
- 큰 문제를 작은 문제로 나누어 해결 → 결과 합쳐 전체 문제 답 얻음
- 재귀 호출 사용 → 시스템 스택 크기가 큰 데이터 정렬 시 제한적
- 분할 리스트 합치는 과정에 추가적 메모리 공간 필요
- 매우 큰 데이터셋 : 메모리 사용량 고려 필요
- 적은 데이터셋 : 삽입 정렬/버블 정렬이 더 효율적
💡 작동 원리
- 분할 (Divide) : 정렬 ❌ 리스트를 계속 절반 나눔 → 각 부분 리스트 크기 1 될 때까지 분할
- 정복 (Conquer) : 각 부분 리스트를 재귀적 정렬
- 결합 (Merge) : 정렬된 부분 리스트들을 하나의 정렬 리스트로 합침
💡 특징
- 시간 복잡도 : 평균
- 공간 복잡도 : 추가 배열 필요
- 안정성 : 안정 정렬
- 효율성 : 추가적인 메모리 공간 필요
💡 구현
def mergeSort(arr):
if len(arr) > 1:
mid = len(arr) // 2
# 분할
L = arr[:mid]
R = arr[mid:]
# 재귀 호출로 계속 분할
mergeSort(L)
mergeSort(R)
i = j = k = 0
while i < len(L) and j < len(R):
if L[i] < R[j]:
arr[k] = L[i]
i += 1
else:
arr[k] = R[j]
j += 1
k += 1
while i < len(L):
arr[k] = L[i]
i += 1
k += 1
while j < len(R):
arr[k] = R[i]
j += 1
k += 1
return arr 6️⃣ 힙 정렬 (Heap Sort)
💡 기본 원리
- 선택 정렬 개선한 정렬 방식
- 완전 이진 트리 이용한 최대 힙(
Max Heap)이나 최소 힙(Min Heap) 트리 구조 활용해 배열 정렬 - ❗️ 핵심
- 최대 힙 특성
- 모든 부모 노드가 자기 자식 노드보다 큰 값을 갖는다
→ 배열의 최댓값(or 최솟값) 쉽게 추출
- 모든 부모 노드가 자기 자식 노드보다 큰 값을 갖는다
- 최대 힙 특성
💡 작동 원리
- 힙 구성 (Heapify)
- 주어진 배열로부터 최대 힙 구성
- 배열 중간부터 시작해 처음까지 역순 진행
- 각 요소에 대해 하위 힙을 최대 힙으로 만드는 작업 반복
- 정렬 실행
- 최대 힙의 루트(가장 큰 값)와 마지막 요소 교환
- 마지막 요소 제외한 나머지 힙에 대해 다시 힙 구성 과정 실행
- 모든 요소 정렬될 때까지 반복
💡 특징
- 시간 복잡도 : 평균 및 최악 보장
- 공간 복잡도 : → In-place 정렬, 추가 배열 사용 ❌
- 안정성 : 불안정 정렬
- 효율성 : 대용량 데이터 처리에 적합, 추가적인 메모리 할당 ❌
| 장점 | 단점 |
|---|---|
| 모든 경우에 보장해 데이터 많아도 성능 급격 저하 ❌ | 구현 복잡 |
| in-place 정렬 → 추가적 메모리 거의 사용 ❌ | 불안정 정렬 |
| 최악에도 안정적인 성능 | 다른 정렬 알고리즘 비해 상대적으로 느림 (퀵 정렬이 더 빠름) |
💡 구현
def heapify(arr, n, i):
largest = i # 루트를 최댓값으로 가정
left = 2 * i + 1 # 왼쪽 자식
right = 2 * i + 2 # 오른쪽 자식
# 왼쪽 자식이 루트보다 크다면
if left < n and arr[left] > arr[largest]:
largest = left
# 오른쪽 자식이 현재 최댓값보다 크다면
if right < n and arr[right] > arr[largest]:
largest = right
# 최댓값이 루트가 아니라면 교환
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
# 교환된 루트에 대해 다시 힙 구성
heapify(arr, n , largest)
def heapSort(arr):
n = len(arr)
# 초기 최대 힙 구성
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
# 하나씩 원소 꺼내서 다시 최대 힙 구성
for i in range(n-1, 0, -1):
arr[i], arr[0] = arr[0], arr[i]
# 루트와 마지막 요소 교환
heapify(arr, i, 0)7️⃣ 계수 정렬 (Counting Sort)
💡 기본 원리
- 비교하지 않는 정렬 방법
- 주어진 배열 내 각 요소가 몇 번 등장하는지 세어서 정렬
- 특정 조건 만족 시, 훨씬 뛰어난 성능
- 적용 범위, 환경 잘 이해하고 사용하면 매우 효율적
- 소규모 범위 내 정수 대량 정렬 시, 데이터 분포 분석 시
💡 작동 원리
- 입력 배열의 요소 범위 확인 : 가장 큰 요소 찾아 그 기반으로 카운트 배열 크기 결정
- 카운트 배열 초기화 & 데이터 세기 : 모든 요소 세어 카운트 배열 값 증가
- 누적 카운트 배열 계산 : 카운트 배열 순차적 더함 → 각 요소가 출력 배열에서 몇 번째 위치에 있어야 하는지 결정
- 결과 배열 만들기 : 입력 배열 반복 & 카운트 배열 참조 → 각 요소 결과 배열을 올바른 위치에 배치
- 결과 복사 : 필요한 경우, 결과 배열 내용을 입력 배열에 복사
💡 특징
- 시간 복잡도 : →
n배열 크기,k입력 데이터 범위
- 안정성 : 안정 정렬
- 효율성 : 데이터 범위 넓을수록 메모리 사용량 크게 증가
| 장점 | 단점 |
|---|---|
| 데이터 범위 한정적 & 데이터 크기 클 경우 → 빠른 정렬 속도 | 주로 정수 등 제한된 데이터 유형에서만 사용 가능 |
| 안정 정렬(Stable Sort) | 문자열/복잡한 객체같은 데이터 유형에 직접 적용 어려움 |
| 계수 정렬 과정에서 데이터에 대한 추가적 정보(데이터 분포 등) 얻기 가능 → 다른 알고리즘에서 유용 활용 | 데이터 최댓값 매우 클 경우, 상응하는 카운트 배열 필요 → 메모리 사용량 많아짐 |
💡 구현
def counting_sort(arr):
# 최대값 찾기
max_val = max(arr)
# 카운트 배열 초기화
count_arr = [0] * (max_val + 1)
# 입력 배열의 요소 세기
for num in arr:
count_arr[num] += 1
# 누적 카운트 배열 계산
for i in range(1, len(count_arr)):
count_arr[i] += count_arr[i-1]
# 결과 배열 초기화
output_arr = [0] * len(arr)
# 결과 배열 만들기
i = len(arr) - 1
while i >= 0:
output_arr[count_arr[arr[i]] - 1] = arr[i]
count_arr[arr[i]] -= 1
i -= 1
# 결과 복사
for i in range(len(arr)):
arr[i] = output_arr[i]8️⃣ 팀 정렬 (Tim Sort)
💡 기본 원리
실제 데이터는 대부분 이미 정렬돼 있을 것이다라는 가정에 기반한 알고리즘- 삽입 정렬 + 병합 정렬 적절히 조합
- 실생활 데이터 특성을 고려해 만들어져 현업에서 널리 사용
- 완전히 무작위 보단 일정 패턴 있는 일반적인 데이터에서 빠른 성능
💡 작동 원리
- 전체를 작은 덩어리(
run)로 잘라 각각의 덩어리를 삽입 정렬로 정렬 - 덩어리들을 병합 정렬하여 하나의 덩어리로 만듦
- Galloping : 병합하는 과정에서 추가로 진행하는 최적화 방법
- 계속 참조하는 run을 빠르게 참조하도록 동작
💡 특징
- 시간 복잡도 : 최선 , 최악 및 평균
- 공간 복잡도 :
- 안정성 : 안정 정렬
- 효율성 : 병합 정렬보단 적은 추가 메모리 필요
💡 사용
# sort 함수 이용
arr.sort()
# sorted 함수 이용
sorted_arr = sorted(arr)9️⃣ 기수 정렬 (Radix Sort)
💡 기본 원리
- 정수/문자열과 같은 비교가 아닌 정렬 방식 사용하는 알고리즘
- 정수 정렬에 효율적
- 숫자 같은 특정 유형 데이터에만 적용 가능 → 데이터 유형 확인 필요
- 데이터의 자릿수/문자 위치 기준으로 그룹 나누어 정렬
💡 작동 원리
- 가장 낮은 자릿수부터 시작 → 가장 높은 자릿수까지 순차적 정렬
- 각 자릿수에 대해 안정 정렬 알고리즘(카운팅 정렬)으로 정렬
- 모든 자릿수 정렬 완료 → 전체 데이터 정렬
💡 특징
- 시간 복잡도 : → 자릿수 길이(
k)에 크게 의존n: 정렬할 원소의 수
- 공간 복잡도 : 추가 배열 필요
- 안정성 : 자릿수 고정되어 있어 안정 정렬 수행
- 카운팅 정렬 (Counting Sort)
- 버킷 정렬 (Bucket Sort)
- 효율성 : 추가적 메모리 공간 필요 (각 자릿수별 데이터 임시 저장 위함)
| 장점 | 단점 |
|---|---|
| 데이터의 자릿수/문자의 위치 정보 활용해 정렬 수행 → 특정 조건에서 매우 빠름 | 숫자/문자열 같은 특정 유형의 데이터에만 적용 가능 |
| 안정 정렬 | 추가적 메모리 필요 |
💡 구현
# 카운팅 정렬
def counting_sort(arr, exp1):
n = len(arr)
output = [0] * n
count = [0] * (10)
for i in range(0, n):
index = arr[i] // exp1
count[index % 10] += 1
for i in range(1, 10):
count[i] += count[i - 1]
i = n - 1
while i >= 0:
index = arr[i] // exp1
output[count[index % 10] - 1] = arr[i]
count[index % 10] -= 1
i -= 1
for i in range(0, len(arr)):
arr[i] = output[i]
# 내부적으로 카운팅 정렬하는 기수 정렬
def radix_sort(arr):
max1 = max(arr)
exp = 1
while max1 // exp > 0:
counting_sort(arr, exp)
exp *= 10📖 In-place sorting (제자리 정렬)
정렬 과정에서 추가적인 공간이 필요하지 않은 정렬
📖 Stable sorting (안정적인 정렬)
동일한 값을 가진 원소의 상대적인 순서가 정렬 후에도 유지
= 동일한 값 요소의 상대적 순서 변경 ❌
📖 Unstable sorting (불안정적인 정렬)
값 같은 레코드가 입력에 있을 때, 순서 정렬 후에도 유지되지 않을 수 있음