[파이썬/Python] 백준 7795번: 먹을 것인가 먹힐 것인가

숨·2024년 7월 8일

알고리즘 문제 풀이

목록 보기

20/105

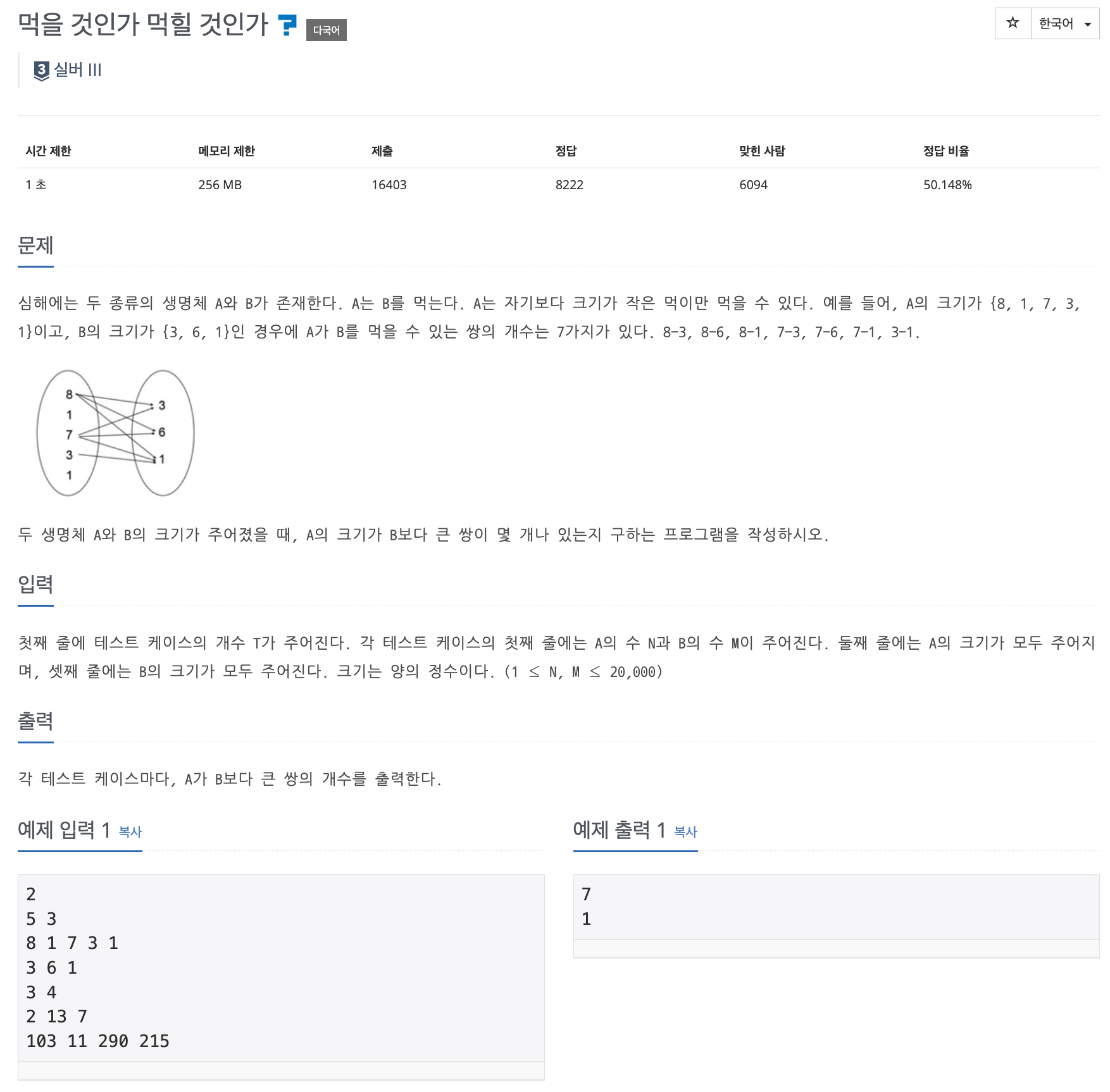
📌 문제 : 백준 7795번

📌 문제 탐색하기

T: 테스트 케이스의 개수
N : A의 수 (1 ≤ N ≤ 20,000)
M : B의 수 (1 ≤ M ≤ 20,000)
A : 자기보다 작은 B를 잡아 먹는 생명체
B : A보다 작으면 잡혀 먹히는 생명체

✅ 입력 조건
1. T 입력
2. N, M 공백 구분해 입력
3. N개의 A들의 크기(양수) 입력
4. M개의 B들의 크기(양수) 입력
✅ 출력 조건
1. 케이스마다 A가 B보다 큰 쌍의 개수 출력

이중 for문으로 A의 요소 하나마다 더 작은 B 요소의 개수를 세면 되지 않을까 싶었지만, 그 방식은 최악의 경우 $O(20,000^2)$ 으로 시간 제한을 넘길 것 같다.

따라서, 이분 탐색을 적용했다.

먼저, 크기를 저장한 두 리스트를 오름차순 정렬한다.

A의 리스트를 돌면서 해당 A보다 작은 B의 개수를 이분 탐색을 통해 계산한다.
작은 B의 개수를 저장할 변수를 정의하여, 이분 탐색이 끝나고 나온 값(a보다 작은 B의 개수)을 더해주면 A와 A보다 작은 B의 조합 개수를 얻을 수 있다.

start, end를 B의 첫번째 인덱스와 마지막 인덱스인 0, M-1로 정의한다.
이분탐색의 종료 조건을 만족할 때까지 while 루프를 돌면서 A의 각 요소별로 작은 B의 개수를 구하고 더한다.

가능한 시간복잡도

A 정렬 → $O(NlogN)$
B 정렬 → $O(MlogM)$
A 요소별 더 작은 B 요소 개수 구하기 → $O(NlogM)$

최종 시간복잡도
$O(NlogM)$ 으로 제한 시간 내에 연산이 가능하다.

알고리즘 선택

A 요소별 B 리스트에서 이분 탐색으로 작은 개수 찾기

📌 코드 설계하기

T 입력
N, M 입력
N개의 A 크기 입력
M개의 B 크기 입력
크기 리스트 정렬
이분 탐색

📌 시도 회차 수정 사항

1회차

📌 정답 코드

import sys

input = sys.stdin.readline

# 1. T 입력
T = int(input())

for _ in range(T):
    # 2. N, M 입력
    N, M = map(int, input().split())

    # 3. N개의 A 크기 입력
    A = list(map(int, input().split()))

    # 4. M개의 B 크기 입력
    B = list(map(int, input().split()))

    # 5. 크기 리스트 오름차순 정렬
    A.sort()
    B.sort()

    # 6. 이분 탐색
    count = 0
    for a in A:
        start, end = 0, M-1
        # 6-1. 이분 탐색 종료 조건
        while start <= end:
            mid = (start + end) // 2
            # B[mid]가 a보다 작은 요소를 더 찾기 위해 배열의 오른쪽 검사
            if B[mid] < a:
                start = mid + 1
            # B[mid]가 a보다 작은 요소를 더 찾기 위해 배열의 왼쪽 검사
            else:
                end = mid - 1
        # 최종 start : B에서 a보다 작은 요소의 개수 의미
        count += start

    # 7. 원하는 형식의 결과 출력
    print(count)

결과

다른 풀이

import sys

input = sys.stdin.readline


# 1. T 입력
T = int(input())

for _ in range(T):
    # 2. N, M 입력
    N, M = map(int, input().split())

    # 3. N개의 A 크기 입력
    A = list(map(int, input().split()))

    # 4. M개의 B 크기 입력
    B = list(map(int, input().split()))

    # 5. 크기 리스트 오름차순 정렬
    A.sort()
    B.sort()

    # 6. 투 포인터
    count = 0
    p2 = 0
    for p1 in range(N):
        while p2 < M and A[p1] > B[p2]:
            p2 += 1
        count += p2

    print(count)