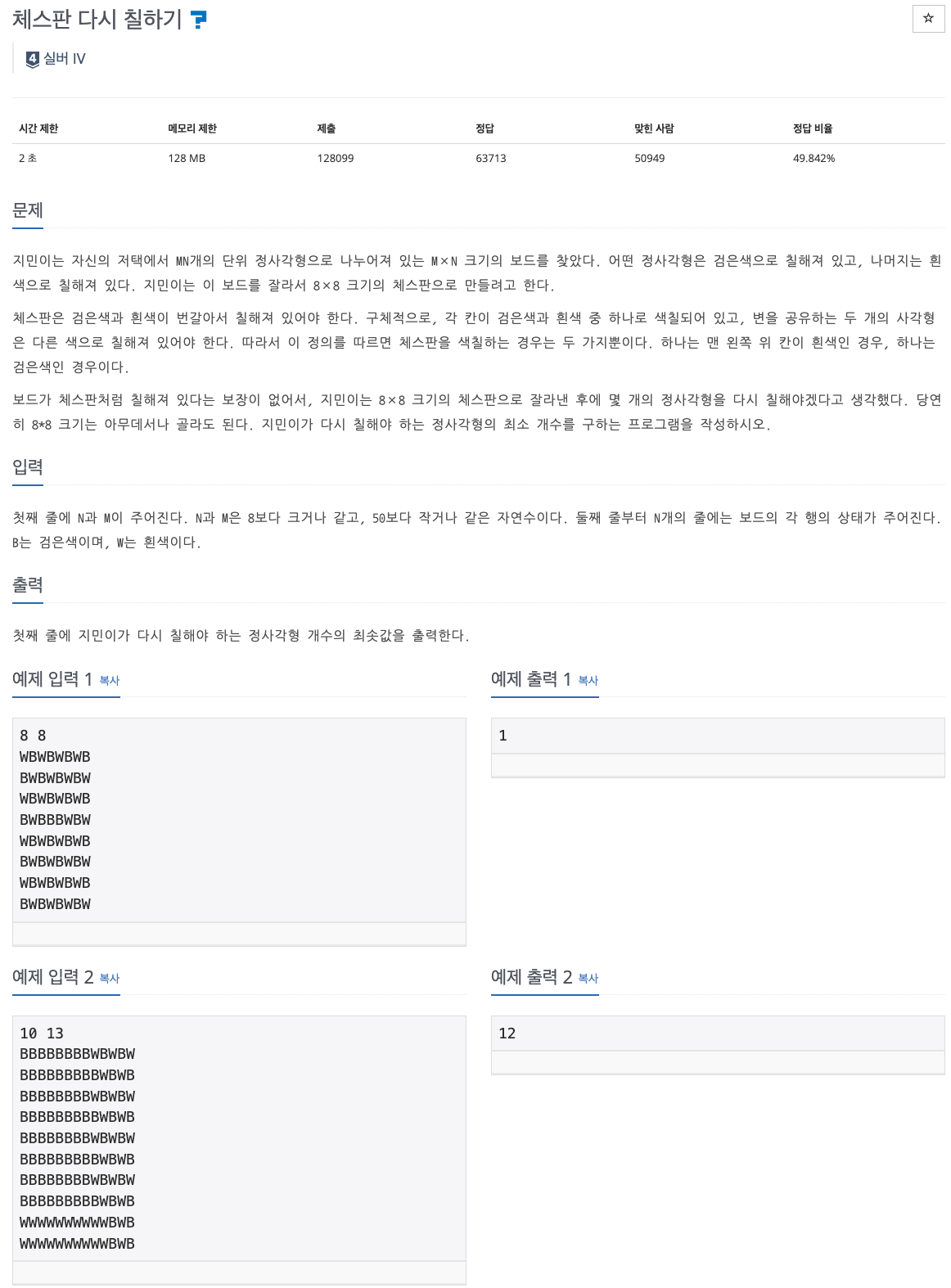
📌 문제 : 백준 1018번
📌 문제 탐색하기
N : 보드의 세로 길이 (8 ≤ N ≤ 50)
M : 보드의 가로 길이 (8 ≤ M ≤ 50)
✅ 입력 조건
1.N,M입력
2.N번 반복해 보드 각 행의 상태 입력
✅ 출력 조건
1. 다시 칠해야 하는 정사각형 개수의 최솟값 출력
2. 8×8 크기의 체스판으로 만들 것
3. 변 공유하는 2개의 사각형은 다른 색이어야 함
4. 색칠하는 경우 : 맨 왼쪽 위가 흰색 또는 검은색 2가지
M, N이 둘다 8보다 크다면 8×8 크기로 잘라가면서 칠해야 하는 정사각형의 최소 개수를 구해야 한다.
색칠하는 경우가 2가지 존재하므로
1. 맨 왼쪽 위가 흰색인 경우
2. 맨 왼쪽 위가 검은색인 경우
를 각각 고려해주어야 한다.
저 2가지 경우에 따라 for문을 통해 덧칠 필요 여부를 확인해 덧칠 횟수를 증가시켜 해당 보드의 총 덧칠 횟수를 구한다.
2가지 중 덧칠 횟수가 더 적은 수를 최소 덧칠 횟수로 갱신한다.
이때 예제로 확인해보면, 결국 둘 중 한가지의 덧칠 횟수는 64에서 다른 덧칠 횟수를 뺀 값과 동일함을 알 수 있다.
이 과정을 다음으로 만들 수 있는 보드에서도 진행하여 덧칠 횟수를 구하고 최소 덧칠 횟수와 비교해서 갱신한다.
즉, 브루트포스 알고리즘으로 하나하나 확인해가며 덧칠 횟수를 세는 방식으로 구현한다.
가능한 시간복잡도
보드 만들기 →
덧칠 횟수 세기 →
최종 시간복잡도
최악의 경우,
N=50, M=50이므로
개의 8×8 보드를 만들게 된다.
for문으로 하나의 보드의 전체 칸을 확인하면 번의 연산이 필요하므로 번의 연산이 필요하다.
이는 최대 2억번 내 연산이 가능하다.
알고리즘 선택
브루트포스로 색을 확인해가며 덧칠 횟수 갱신하기
📌 코드 설계하기
- N, M 입력
- 체스판 입력
- 체스판의 패턴 정의
- 최소 덧칠 횟수 정의
- 보드판 자르기
- 덧칠 횟수 초기화
- 8*8 보드 자르기
- 원하는 형태로 출력
📌 정답 코드
import sys
input = sys.stdin.readline
# N, M 입력
N, M = map(int, input().split())
# 체스판 입력
chess = [input().rstrip() for _ in range(N)]
# 체스판의 패턴 정의
white_first = [
'WBWBWBWB',
'BWBWBWBW',
'WBWBWBWB',
'BWBWBWBW',
'WBWBWBWB',
'BWBWBWBW',
'WBWBWBWB',
'BWBWBWBW'
]
# 최소 덧칠 횟수 정의
min_paint = 64
# 보드판 자르기
for j in range(N-7):
for i in range(M-7):
# 덧칠 횟수 초기화
count = 0
# 8*8 보드 확인
for row in range(8):
for col in range(8):
if chess[j + row][i + col] != white_first[row][col]:
count += 1
# 덧칠 횟수가 더 작은 것을 선택
min_paint = min(min_paint, count, 64-count)
# 원하는 형태로 출력
print(min_paint)- 결과

📌 회고
- 문제 이해도 쉽지 않았는데 구현 과정도 복잡했다. 급한 마음에 키보드부터 누르려고 하지 않고, 문제를 이해하고 조건을 파악하는데 시간을 더 쏟아야겠다고 결심했다.