[파이썬/Python] 백준 1463번: 1로 만들기

숨·2024년 7월 13일

코테

알고리즘 문제 풀이

목록 보기

29/105

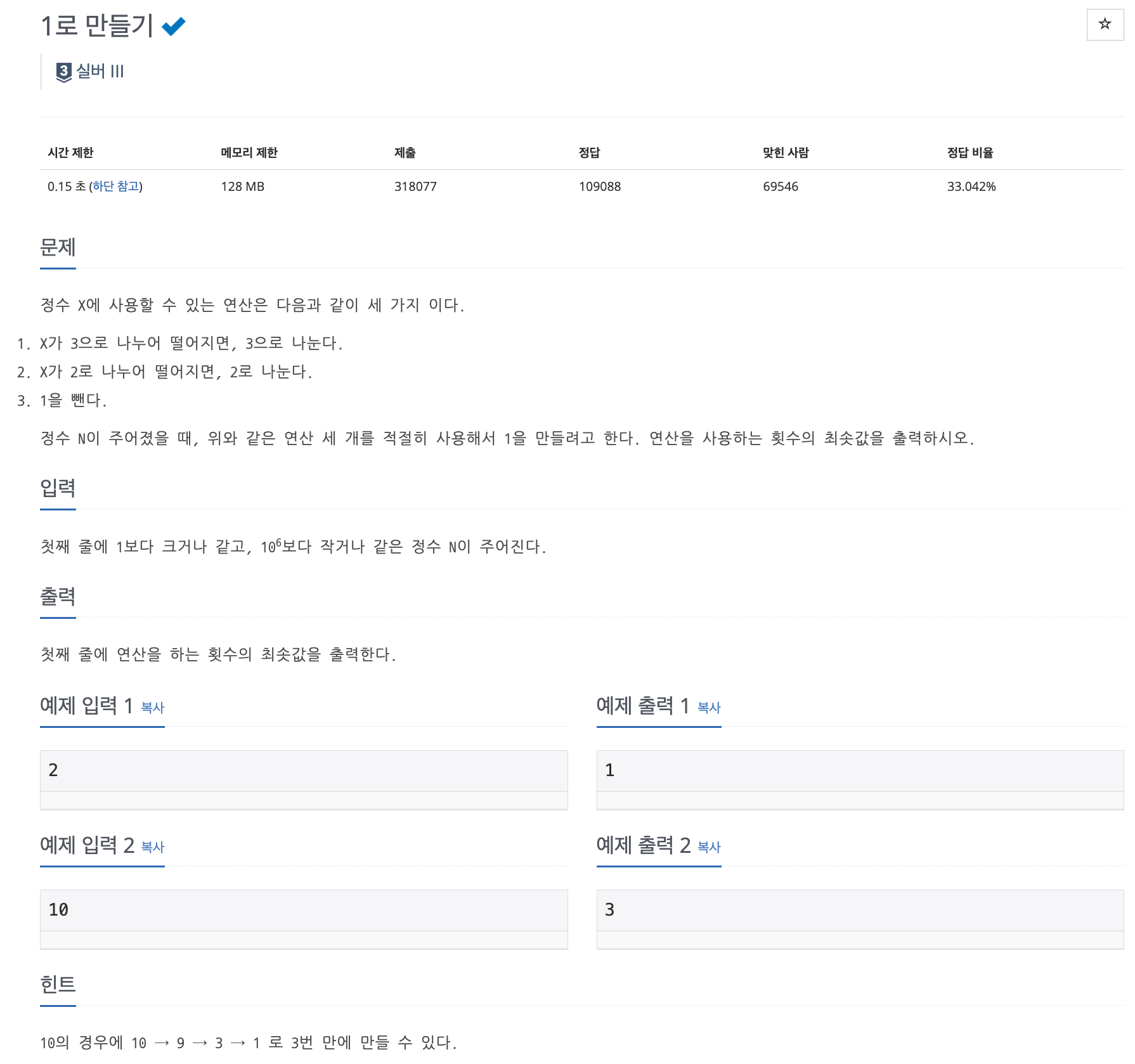
📌 문제 : 백준 1463번

📌 문제 탐색하기

N : 1로 만들 정수 (1 ≤ N ≤ $10^6$ )

✅ 입력 조건
1. N 입력
✅ 출력 조건
1. 1로 만드는 연산 횟수 최솟값 출력
2. 3으로 나누기, 2로 나누기, 1 빼기 → 3가지 연산을 적절히 사용

해당 정수 X에서 연산 횟수 최솟값을 찾는 과정은
연산 과정에서 만들어지는 숫자들의 연산 횟수 최솟값을 찾는 과정을 포함하고 있다.

예제 2의 10 → 9 → 3 → 1 로 만드는 과정에서
10을 1로 만드는 최소 연산 횟수를 구하는 것은
9를 1로 만드는 최소 연산 횟수를 구하는 과정을 활용한다고 할 수 있다.
마찬가지로 9는 3을 1로 만드는 연산을 활용한다.
이전에 얻은 결과를 다음 단계에 활용하므로 DP 문제로 풀 수 있다.

i에서 1로 만드는데 사용하는 연산 횟수를 점화식으로 표현하면,
먼저 1을 빼주는 연산을 고려하여 다음과 같이 표현해준다.
D[i] = D[i-1] + 1

초기값으로 i = 1이면 1로 만드는 연산 횟수는 0임을 이용한다.

2로 나누어 떨어지면 2로 나누고, 3으로 나누어 떨어지는 3으로 나눌 수 있으므로 조건문을 통해 이를 구현해준다.

마지막으로 최소 횟수를 구해야 하므로 연산 후 나온 연산 횟수 숫자가 더 작아야 한다.
따라서 1을 뺀 연산과 2로 나누기 또는 3으로 나누기한 결과 중 더 작은 값으로 DP 테이블을 채워주도록 한다.

가능한 시간복잡도

DP 계산 → $O(N)$

최종 시간복잡도
$O(N)$ 으로 제한 시간 내에 연산이 가능하다.

알고리즘 선택

DP로 계산하기

📌 코드 설계하기

N 입력
dp 테이블 초기화
dp 테이블 채우기

📌 시도 회차 수정 사항

1회차

	# 4-1. 1 빼주는 연산
    D[i] = D[i-1] + 1

    # 4-2. 2로 나누어 떨어지는지 고려
    if D[i] % 2 == 0:
        D[i] = min(D[i], D[i // 2] + 1)

    # 4-3. 3으로 나누어 떨어지는지 고려
    if D[i] % 3 == 0:
        D[i] = min(D[i], D[i // 3] + 1)

예제 2 결과
해당 숫자가 2로 나누어 떨어지는지 또는 3으로 나누어 떨어지는지를 확인해야 하는데, 연산 횟수를 확인해서 잘못된 결과를 얻었다.

    # 4-1. 1 빼주는 연산
    D[i] = D[i-1] + 1

    # 4-2. 2로 나누어 떨어지는지 고려
    if i % 2 == 0:
        D[i] = min(D[i], D[i // 2] + 1)

    # 4-3. 3으로 나누어 떨어지는지 고려
    if i % 3 == 0:
        D[i] = min(D[i], D[i // 3] + 1)

조건문에서 숫자를 확인하도록 변경하여 해결하였다.

📌 정답 코드

import sys

input = sys.stdin.readline

# 1. N 입력
N = int(input())

# 2. dp 테이블 초기화
D = [0] * 1000001

# 3. dp 테이블 초기값 고려
D[1] = 0

# 4. dp 테이블 채우기
for i in range(2, N+1):
    # 4-1. 1 빼주는 연산
    D[i] = D[i-1] + 1

    # 4-2. 2로 나누어 떨어지는지 고려
    if i % 2 == 0:
        D[i] = min(D[i], D[i // 2] + 1)

    # 4-3. 3으로 나누어 떨어지는지 고려
    if i % 3 == 0:
        D[i] = min(D[i], D[i // 3] + 1)

# 5. 원하는 형식으로 출력
print(D[N])