[파이썬/Python] 백준 10422번: 괄호

숨·2025년 1월 6일

코테

알고리즘 문제 풀이

목록 보기

91/105

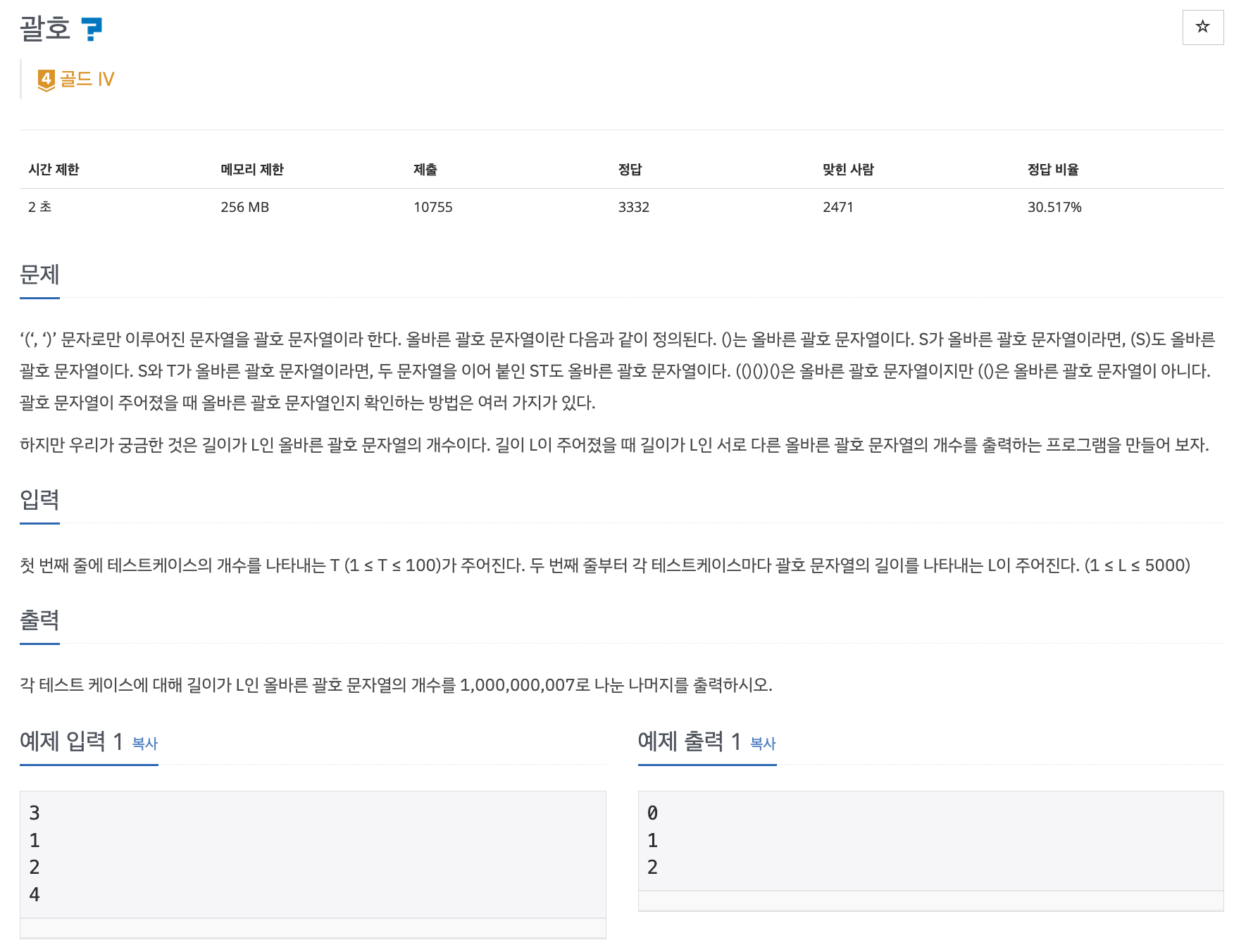
📌 문제 : 백준 10422번

📌 문제 탐색하기

T : 테스트케이스 개수 $(1 ≤ T ≤ 100)$
L : 괄호 문자열의 길이 $(1 ≤ L ≤ 5000)$

문제 풀이

입력은 (, ) 문자로만 이루어진 괄호 문자열이다.

각 테스트케이스에 대해 길이가 L인 올바른 괄호 문자열 개수를 센 후, 그 수를 1000000007로 나눈 나머지를 구해야 한다.

⭐️ 올바른 괄호의 기준

괄호의 짝이 제대로 이루어진 경우

짝이 맞는다면 L은 무조건 짝수이어야만 함

L이 홀수 → 무조건 올바른 괄호 문자열 0개

올바른 괄호 문자열끼리 붙여도 올바른 괄호 문자열 ‼️

L이 짝수인 경우에 한해 가능한 올바른 괄호 문자열을 구하면 다음과 같다.

L=2 → 1개
()

L=4 → 2개
()()
(())

L=6 → 5개
()()()
(())()
()(())
(()())
((()))

L=8 → 14개
()()()()
(())()()
()(())()
(()())()
((()))()
()()(())
(())(())
()((()))
()(()())
(()()())
((())())
(()(()))
((()()))
(((())))

위에서 언급한 올바른 괄호의 기준처럼 올바른 괄호 문자열은 이전 짝수 단계의 문자열들을 활용해 만들 수 있다.

L이 증가할 때마다 괄호쌍 ()가 하나씩 증가시킨다고 할 때, 올바른 괄호 문자열이 들어갈 수 있는 2가지 위치가 존재한다.

괄호 안
괄호 밖

이 2가지 위치에 이전 L에서 구한 올바른 괄호 문자열을 배치하면 될 것이다.

현재 L=8이라면 2가지 위치에
1. L=6 & L=0
2. L=4 & L=2
3. L=2 & L=4
4. L=0 & L=6
라는 4가지 경우가 발생한다.
(L=0엔 괄호가 없으므로 올바른 괄호 문자열이라 간주)

각각의 경우에서 발생하는 경우의 수를 계산해서 모두 합한다면 원하는 답을 얻을 수 있을 것이다.

앞의 결과를 이용해 답을 구할 수 있으므로 점화식으로 표현한다면 다음과 같다.
dp[i] = dp[0] * d[i-2] + dp[2] * dp[i-4] + ... + dp[i-2] * dp[0]

크기가 5000이면서 0으로 채워진 dp 테이블을 정의한다.
dp[0] = 1로 초기화한다.
누적합을 구하기 위해 이중 for문을 통해 점화식을 계산하여 테이블을 채운다.

가능한 시간복잡도

dp 테이블 채우기 → $O(\frac{5000}{2}) * O(\frac{\frac{5000}{2}+1}{2}) = O(2500*1250)$

최종 시간복잡도
최악의 경우 $O(3125000)$ 이 되어, 2초 내에 연산 가능하다.

알고리즘 선택

DP 알고리즘 활용

📌 코드 설계하기

dp 테이블 정의
dp 테이블 초기화
점화식으로 짝수에만 dp 테이블 채우기
테스트케이스 개수 입력
테스트케이스만큼 반복
5-1. L 입력
5-2. 결과 출력

📌 시도 회차 수정 사항

1회차

시간 초과 발생
혹시 dp 테이블의 크기를 L의 최댓값으로 해서 그런 것인가라는 생각에 입력받은 L로 바꾸어봤지만 같은 결과였다. 그리고 이미 시간복잡도에서 가능한 것을 알았기 때문에 의미없는 수정이었다.
테스트케이스마다 계산해야 한다고 생각해서 dp 테이블을 채우는 과정을 함수로 만들어 매번 호출하는 식으로 작성한 것이 원인이었다. dp 테이블을 한번에 채우고 바로 필요한 값을 구하는 것이 dp의 장점인데 큰 실수를 했다.

2회차

인덱스 에러 발생
1회차 에러 해결 전에 발생했는데 에러 해결 후 해결되었다.

📌 정답 코드

import sys

input = sys.stdin.readline

# dp 테이블 정의
dp = [0] * 5001

# dp 테이블 초기화
dp[0] = 1

# 점화식으로 짝수에만 dp 테이블 채우기
for n in range(2, 5001, 2):
    for i in range(2, n + 1, 2):
        dp[n] += dp[i - 2] * dp[n - i]

        # 1000000007로 나눈 값 저장
        dp[n] %= 1000000007


# 테스트케이스 개수 입력
T = int(input())

# 테스트케이스만큼 반복
for _ in range(T):
    # L 입력
    L = int(input())

    # 결과 출력
    print(dp[L])